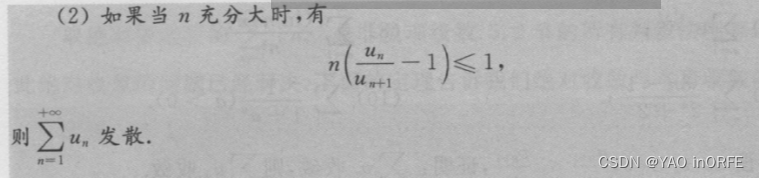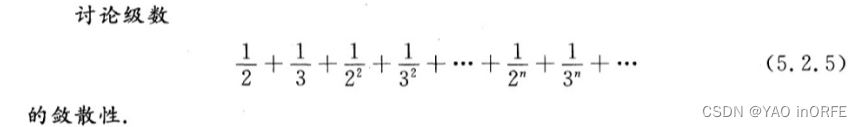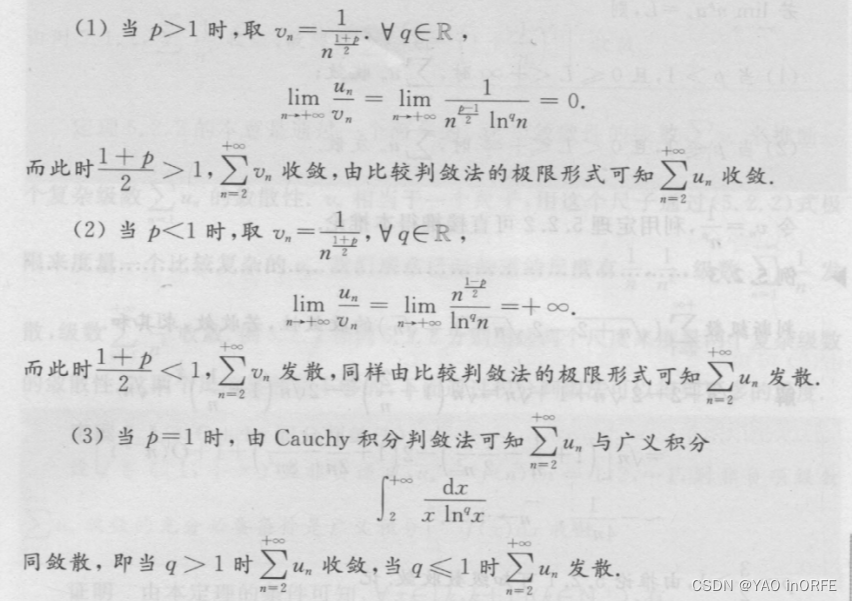提示：本文的适用对象为已修过《微积分A1》的非数学系学生，文中题型方法为个人总结，为个人复习使用。部分理解虽然不太严谨，但对于解题的实用性较强。若有疏漏or错误，欢迎批评指正。

1.（通过无穷级数的前n项和来判断）若一个无穷级数的前n项和收敛于S，则这个无穷级数也收敛于S；反之若其前n项和的极限不存在，则称级数发散。

2.（通过Cauchy准则来判断）若一个无穷级数存在一个界限N,当n>N时，从n+1到任意的n+p项求和取绝对值，其结果比任何一个大于零的数都要小，则该无穷级数收敛。

反之，证明发散性可以用Cauchy准则的逆定理，超级简单！！！！叙述如下：

,都有。这样我们就可以只要取出一组这样的值满足情况就能证明无穷级数发散 

3.一个想法就是：部分和是单调有界数列推出部分和收敛，进而推出原级数收敛

4.记住：在公比绝对值小于一的时候，等比级数收敛；在p>1时，级数收敛 

1.若无穷级数收敛，则在n趋向于正无穷的时候，级数的值趋向于0。

2.两级数都收敛，则由其线性组合成的新级数也收敛，但是无法反推

3.两发散级数的组合未必发散，但一收敛一发散组合必发散

4.收敛级数的收敛性不会因为改变有限项的值而改变，但是收敛值一般会改变 

1.（比较判敛法）大的收敛，小的就收敛。小的发散，大的就发散

2.（比较判敛法的极限形式）

 一些判断复杂级数收敛性的方法，找到此级数的同阶简单级数，看简单级数的收敛性

3.（比值判别法）后项与前项做比值取极限，极限值（或上极限）小于1，则级数收敛；极限值大于1（或下极限），则级数发散。

4.（根值判别法）对级数开n次根号取极限（上极限），极限值小于1，则级数收敛；极限值大于1，则级数发散。

5.（Raabe判别法）

嗯...这个方法感觉是针对很精细的差异进行判断的

6. （Cauchy积分判敛法）

级数是离散的函数，若一个级数对应的函数f(x)非负递减，怎级数收敛的充分必要条件是广义积分收敛 

这个定理比较突出的一点是，它可以把广义积分的收敛性与非负项级数的收敛性联系起来，许多在广义积分中的“尺子”都可以被用于判断级数收敛。

1、关于奇数项和偶数项的级数

 方法1：使用“求和极限”，求出2n项和2n-1项的和的极限，最后得出这两个极限相等，推出级数收敛

方法2：使用根式判敛法分别判断奇数项和偶数项的敛散性，发现极限值都小于1，则推出级数收敛。

2、对于一个特殊尺子敛散性的衡量

对于

核心思想：1、关于P分类讨论，分别讨论p>1,p