Dijkstra求最短路(常见疑惑解答 + 代码模板) |
您所在的位置:网站首页 › 最短路问题的常见算法是什么名字 › Dijkstra求最短路(常见疑惑解答 + 代码模板) |
Dijkstra求最短路(常见疑惑解答 + 代码模板)
Dijkstra算法讲解
一、概念详解二、算法详解1. 区分情况2. 时间复杂度3. 正负无穷4. 邻接表构造① 为什么会使用数组构造邻接表?② 如何用数组构造邻接表?
5. 进行堆优化6. 代码模板
 苟蒻小白发文,邻接表讲解引用
大佬文章,有任何不足欢迎大佬在评论区交流和斧正~觉得文章写的可以的请点赞👍或收藏⭐下 vo(〃^▽^〃)o~
一、概念详解
苟蒻小白发文,邻接表讲解引用
大佬文章,有任何不足欢迎大佬在评论区交流和斧正~觉得文章写的可以的请点赞👍或收藏⭐下 vo(〃^▽^〃)o~
一、概念详解
Dijkstra算法又称迪杰斯特拉算法,应用于图的结构中。 应用场景: 解决无负权图的最短路径问题,只能应付单源起点的情况 (特别强调:既可以是无向图,也可以是有向图,有些博主只说是有向图) 算法本质: 贪心思想 正确性: 该算法的正确性是基于当所有边长都是非负数的时候,全局最小值不可能再被其他节点更新了,我们不断用当前全局最小值进行松弛可以保证正确性 应用示例: 计算机网络传输的问题中,怎样找到一种最经济的方式,从一台计算机向网上所有其它计算机发送一条消息 二、算法详解 1. 区分情况一般我们认为,n(点数)和m(边数) 同数量级时为稀疏图,m大于n2为稠密图 稠密图用邻接矩阵,稀疏图用邻接表 2. 时间复杂度朴素版的时间复杂度为 O(n2) for (int i = 0; i O(m) heap.pop(); int ver = t.second, distance = t.first; if (st[ver])continue; st[ver] = true; //O(m) * O(1) -> O(m) for (int i = h[ver]; i != -1; i = ne[i]) { int j = e[i]; if (dist[j] > distance + w[i]) { dist[j] = distance + w[i]; heap.push({dist[j], j}); // 堆的插入操作时间复杂度是 O(log(n)) // O(m) * O(log(n)) -> O(mlog(n)) } } } 3. 正负无穷我们经常在定义邻接表 / 邻接图中会使用到正无穷或负无穷去初始化,而在算法竞赛中 通常用 0x3f 代表某个字节的最大值,用 0xcf 代表某个字节的最小值,如int a变量想定义为最大值,则应该给4个0x3f来代表最大值,则int a = 0x3f3f3f3f 为什么不使用INT_MAX / INT_MIN 来作为最大值或最小值呢?原因是:以INT_MAX为无穷大常常面临一个问题,即加一个其他的数会溢出,而这种情况在动态规划,或者其他一些递推的算法中常常出现,很有可能导致算法出问题,INT_MIN也同理 4. 邻接表构造 有些同学看不懂下面代码模板中的用数组构造邻接表矩阵,那咱们来仔细回顾下相关的知识点 4 5 1 4 9 4 3 8 1 2 5 2 4 6 1 3 7 第一行两个整数n m。n表示顶点个数(顶点编号为1~n),m表示边的条数。接下来m行表示,每行有3个数x y z,表示顶点x到顶点y的边的权值为z。下图就是一种使用链表来实现邻接表的方法 第一个原因是:方便操作,效率高,实际应用中非常容易实现的方法 第二个原因是:若使用链表,对于痛恨指针的朋友来说简直是噩梦😱 ② 如何用数组构造邻接表? 首先我们按照读入的顺序为每一条边进行编号(1~m)。比如第一条边“1 4 9”的编号为1,“1 3 7”这条边编号为5。这里用u、v和w三个数组用来记录每条边的具体信息,即u[i]、v[i]和w[i]表示第i条边是从第u[i]号顶点到v[i]号顶点,权值为w[i] 读入第1条边(1 4 9),将这条边的信息存储到u[1]、v[1]和w[1]中。同时为这条边赋予一个编号,因为这条边是最先读入的,存储在u、v和w数组下标为1的单元格中,因此编号就是1。这条边的起始点是1号顶点,因此将first[1]的值设为1 另外这条“编号为1的边”是以1号顶点(即u[1])为起始点的第一条边,所以要将next[1]的值设为-1。也就是说,如果当前这条“编号为i的边”,是我们发现的以u[i]为起始点的第一条边,就将next[i]的值设为-1 我们通过学习朴素版的Dijkstra算法后,了解到朴素算法的实现是从头到尾扫一遍点找出最小的点然后进行松弛(因此需要进行n次迭代)。这个扫描操作就是坑害朴素算法时间复杂度的罪魁祸首。所以我们使用小根堆,用优先队列来维护这个“ 最小的点 ”,从而大大减少算法的时间复杂度。 接下来我们思考一些细节性的问题: ① 提出问题:我们需要往优先队列中push最短路长度,但是它一旦入队,就会被优先队列自动维护离开原来的位置,换言之,我们无法再把它与它原来的点对应上,也就是说没有办法形成点的编号到点权的映射。 ② 解决问题:pair是C++自带的二元组。我们可以把它理解成一个有两个元素的结构体。更刺激的是,这个二元组有自带的排序方式:以第一关键字为关键字,再以第二关键字为关键字进行排序。所以,我们用二元组的first位存距离,second位存编号即可。 ③ 浅入理解:我们发现裸的优先队列其实是大根堆,我们如何让它变成小根堆呢?有两种方法,该文章的模板采取的是第一种方法,第一种是把first位取相反数存入,若需操作first位的话在取出时取相反数就行了(如果不需操作first位则无影响)。第二种是重新定义优先队列(如下代码): priority_queue q;④ 深入理解:解决了上面的问题,我们愉快地继续往下写,后来发现,写到松弛的时候,我们很显然要把松弛后的新值也压入优先队列中去,这样的话,我们又发现一个问题:优先队列中已经存在一个同样编号的二元组(即第二关键字相同),我们没有办法删去它,也没有办法更新它。那么在我们的队列和程序运行的时候,一定会出现bug。怎么办呢??我们在进入循环的时候就开始判断:如果有和堆顶重复的二元组,就直接pop掉,成功维护了优先队列元素的不重复。 6. 代码模板朴素版Dijkstra(即采用邻接矩阵) 👉对应题目:Acwing → 应用 → AC sacber → 训练模式 → 图论 → 单源最短路初级 → 851 注意:做题时应该判断时稠密图,还是稀疏图 👉PTA - L2-001记录路径与计数的练习题:点我跳转 const int N=510; int g[N][N]; //稠密图所以用邻接矩阵存储,表示i点和j点之间边的长度 int dist[N]; //每一个点到源点的距离 bool st[N]; //记录该点的最短距离是否已经确定 int n,m; int Dijkstra() { memset(dist, 0x3f,sizeof dist); //初始化距离 0x3f代表无穷大 dist[1]=0; //第一个点到自身的距离为0 for(int i=0;i dist[t] + w[i] /** if (dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; cnt[j] = cnt[t] pre[j] = t; // 记录路径 } else if (dist[j] == dist[t] + w[i]) { cnt[i] += cnt[t]; //最短路计数 //在这个地方,得按题目要求写条件来记录路径,因为我们要满足条件情况才是我们所需的路径,如果没有条件要求,可不进行记录路径 //如 PTA - L2-001题目的条件是最大救援数量,条件如下 //if (sum[j] < sum[t] + w[i]) { sum[j] = sum[t] + w[i]; pre[j] = t; } } */ } if(dist[n] == 0x3f3f3f3f) return -1; //若第n个点路径为无穷大则不存在最短路径 return dist[n]; } int main() { cin >> n >> m; memset(g, 0x3f, sizeof g); //初始化图,求最短路径,初始为无限大 while(m--) { int x, y, z; cin >> x >> y >> z; g[x][y] = min(g[x][y], z); //发生重边的情况则保留最短的一条边 } cout > m; while (m--) { int a, b, c; cin >> a >> b >> c; add(a, b, c); } cout |
【本文地址】
今日新闻 |
推荐新闻 |
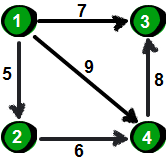
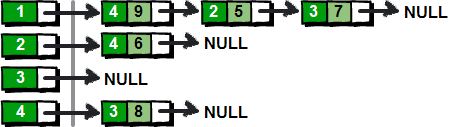
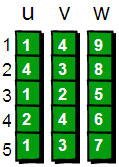 用一个first数组来存储每个顶点其中一条边的编号。以便待会我们来枚举每个顶点所有的边(你可能会问:存储其中一条边的编号就可以了?不可能吧,每个顶点都需要存储其所有边的编号才行吧!甭着急,继续往下看)。比如1号顶点有一条边是 “1 4 9”(该条边的编号是1),那么就将first[1]的值设为1。如果某个顶点i没有以该顶点为起始点的边,则将first[i]的值设为-1,现在我们来看看具体如何操作 前提说明:这里的first数组对应代码模板中的 h[a] 数组,next数组对应 ne[idx] 数组,代码不懂就结合这些看下去
用一个first数组来存储每个顶点其中一条边的编号。以便待会我们来枚举每个顶点所有的边(你可能会问:存储其中一条边的编号就可以了?不可能吧,每个顶点都需要存储其所有边的编号才行吧!甭着急,继续往下看)。比如1号顶点有一条边是 “1 4 9”(该条边的编号是1),那么就将first[1]的值设为1。如果某个顶点i没有以该顶点为起始点的边,则将first[i]的值设为-1,现在我们来看看具体如何操作 前提说明:这里的first数组对应代码模板中的 h[a] 数组,next数组对应 ne[idx] 数组,代码不懂就结合这些看下去 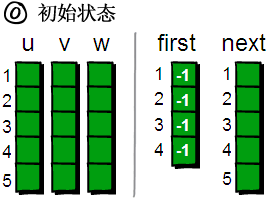
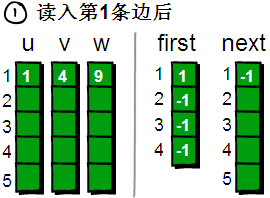
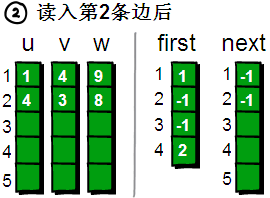 读入第2条边(4 3 8),将这条边的信息存储到u[2]、v[2]和w[2]中,这条边的编号为2。这条边的起始顶点是4号顶点,因此将first[4]的值设为2。另外这条“编号为2的边”是我们发现以4号顶点为起始点的第一条边,所以将next[2]的值设为-1
读入第2条边(4 3 8),将这条边的信息存储到u[2]、v[2]和w[2]中,这条边的编号为2。这条边的起始顶点是4号顶点,因此将first[4]的值设为2。另外这条“编号为2的边”是我们发现以4号顶点为起始点的第一条边,所以将next[2]的值设为-1 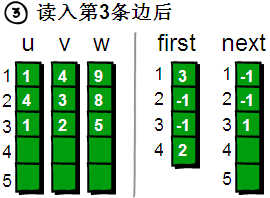 读入第3条边(1 2 5),将这条边的信息存储到u[3]、v[3]和w[3]中,这条边的编号为3,起始顶点是1号顶点。我们发现1号顶点已经有一条“编号为1 的边”了,如果此时将first[1]的值设为3,那“编号为1的边”岂不是就丢失了?解决办法是将next[3]的值设为1即可。现在你知道next数组是用来做什么的吧。next[i]存储的是“编号为i的边”的“前一条边”的编号。(注:next数组的大小由边的数目决定,first数组的大小由顶点的个数来决定)
读入第3条边(1 2 5),将这条边的信息存储到u[3]、v[3]和w[3]中,这条边的编号为3,起始顶点是1号顶点。我们发现1号顶点已经有一条“编号为1 的边”了,如果此时将first[1]的值设为3,那“编号为1的边”岂不是就丢失了?解决办法是将next[3]的值设为1即可。现在你知道next数组是用来做什么的吧。next[i]存储的是“编号为i的边”的“前一条边”的编号。(注:next数组的大小由边的数目决定,first数组的大小由顶点的个数来决定) 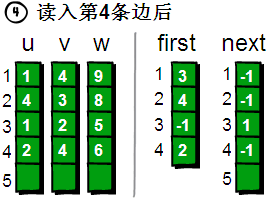 读入第4条边(2 4 6),将这条边的信息存储到u[4]、v[4]和w[4]中,这条边的编号为4,起始顶点是2号顶点,因此将first[2]的值设为4。另外这条“编号为4的边”是我们发现以2号顶点为起始点的第一条边,所以将next[4]的值设为-1
读入第4条边(2 4 6),将这条边的信息存储到u[4]、v[4]和w[4]中,这条边的编号为4,起始顶点是2号顶点,因此将first[2]的值设为4。另外这条“编号为4的边”是我们发现以2号顶点为起始点的第一条边,所以将next[4]的值设为-1 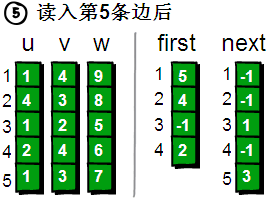 读入第5条边(1 3 7),将这条边的信息存储到u[5]、v[5]和w[5]中,这条边的编号为5,起始顶点又是1号顶点。此时需要将first[1]的值设为5,并将next[5]的值改为3 (编号为5的边的前一条边的编号为3) 此时,如果我们想遍历1号顶点的每一条边就很简单了。1号顶点的其中一条边的编号存储在first[1]中,其余的边则可以通过next数组寻找到。请看下图
读入第5条边(1 3 7),将这条边的信息存储到u[5]、v[5]和w[5]中,这条边的编号为5,起始顶点又是1号顶点。此时需要将first[1]的值设为5,并将next[5]的值改为3 (编号为5的边的前一条边的编号为3) 此时,如果我们想遍历1号顶点的每一条边就很简单了。1号顶点的其中一条边的编号存储在first[1]中,其余的边则可以通过next数组寻找到。请看下图 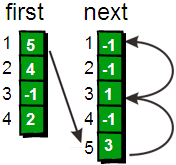 细心的同学会发现,此时遍历边某个顶点边的时候的遍历顺序正好与读入时候的顺序相反。因为在为每个顶点插入边的时候都直接插入“链表”的首部而不是尾部。不过这并不会产生任何问题,这正是这种方法的其妙之处
细心的同学会发现,此时遍历边某个顶点边的时候的遍历顺序正好与读入时候的顺序相反。因为在为每个顶点插入边的时候都直接插入“链表”的首部而不是尾部。不过这并不会产生任何问题,这正是这种方法的其妙之处