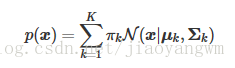【机器学习】10、最大熵模型与EM算法 |
您所在的位置:网站首页 › 最大熵算法模型 › 【机器学习】10、最大熵模型与EM算法 |
【机器学习】10、最大熵模型与EM算法
|
文章目录
一、最大熵模型1、熵联合熵和条件熵相对熵交叉熵互信息总结
2、最大熵模型
二、EM算法(期望最大化算法)三、GMM
一、最大熵模型
l n x < = x − 1 lnx0 f(x)=x−1−lnx,x>0,求导是凸函数,在x=1处取得极值 熵是信息的度量,与信息量成反比。 信息量: h ( x i ) = l o g 2 1 p ( x i ) h(x_i)=log_2\frac{1}{p(x_i)} h(xi)=log2p(xi)1 事件发生的概率越高,对应的信息量越低,事件发生的概率越小,对应的信息量越大。 熵是信息量的期望:
H
(
x
)
=
−
∑
i
=
1
n
p
(
x
i
)
l
o
g
2
1
p
(
x
i
)
H(x)=-\sum_{i=1}^np(x_i)log_2\frac{1}{p(x_i)}
H(x)=−∑i=1np(xi)log2p(xi)1
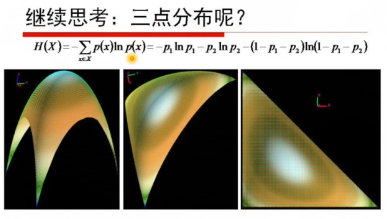
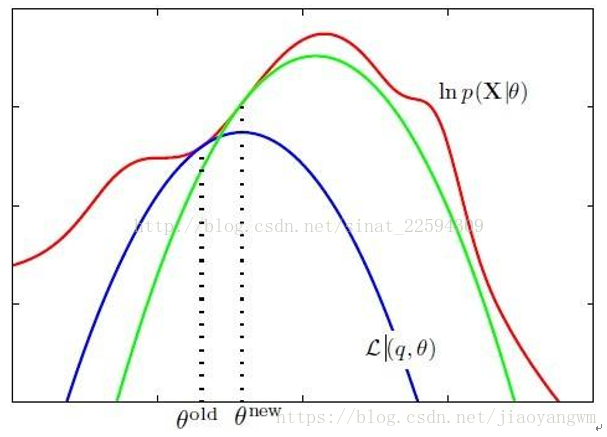
三点分布: p1=p2=p3的时候,曲面的值最高(图1) 当X满足均匀分布时,熵最大: 联合熵:H(X,Y),表示X,Y同时发生的不确定性 H ( X , Y ) = − ∑ ∑ p ( x i , y i ) l o g 2 p ( x i , y i ) = H ( X ) + H ( Y ∣ X ) H(X,Y)=-\sum \sum p(x_i,y_i)log_2 p(x_i,y_i)=H(X)+H(Y|X) H(X,Y)=−∑∑p(xi,yi)log2p(xi,yi)=H(X)+H(Y∣X) 解释:联合熵=X发生的熵+X发生的条件下Y发生的熵 联合熵的性质: 联合熵>=变量熵中最大的联合熵 l n L ( θ n ) ) lnL(\theta_{n+1})>lnL(\theta_n)) lnL(θn+1)>lnL(θn)),迭代若干次,就是渐渐逼近最优解。l n L ( θ ) − l n L ( θ n ) ≥ Q ( θ ∣ θ n ) lnL(\theta)-lnL(\theta_n) \geq Q(\theta|\theta_n) lnL(θ)−lnL(θn)≥Q(θ∣θn)
Q
(
θ
∣
θ
n
)
Q(\theta|\theta_n)
Q(θ∣θn)被称为下确界函数,我们要使得
l
n
L
(
θ
)
lnL(\theta)
lnL(θ)尽可能的大,就要使得
Q
(
θ
∣
θ
n
)
Q(\theta|\theta_n)
Q(θ∣θn)尽可能的大,所以我们每次求得下确界函数的极大值(求偏导=0,得到极大值),将该极大值带入似然函数,求得新的下确界函数,一直迭代到
∣
∣
θ
n
+
1
−
θ
n
∣
∣
≤
ξ
||\theta_{n+1}-\theta_n || \leq \xi
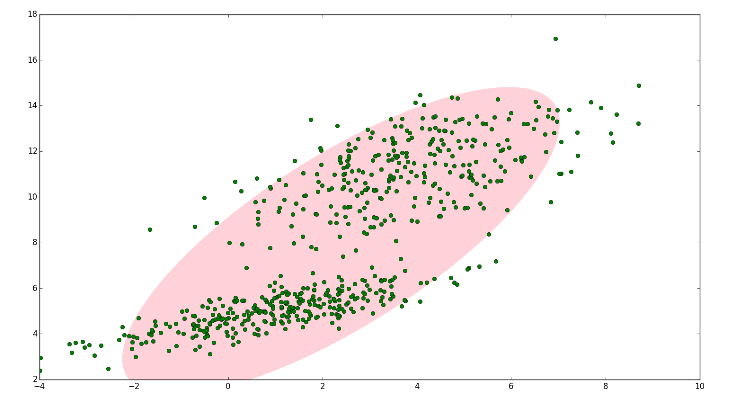
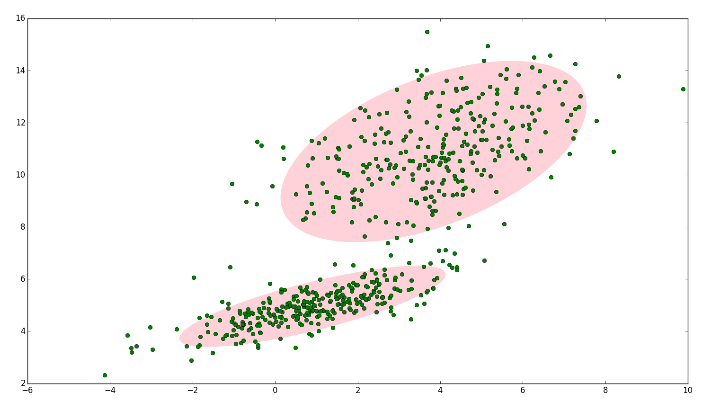
∣∣θn+1−θn∣∣≤ξ,得到的参数即为最优参数。 红色那条线就是我们的对数似然函数,蓝色那条是我们在当前参数下找到的对数似然的下界函数,可以看到,我们找到它的局部极值那么参数更新成thetanew,此时对数似然函数的值也得到了上升,这样重复进行下去,是不是就可以收敛到对数似然函数的一个局部极值了嘛。对的,局部极值 EM算法思想: 含有隐含项的最大似然函数难求解–>求得下边界函数的极值->将其看做此时的函数参数–>得到新的似然函数–>再次得到新的下边界曲线–>迭代至收敛 1 拿到所有的观测样本,根据先验或者喜好先给一个参数估计。 2 根据这个参数估计和样本计算类别分布Q,得到最贴近对数似然函数的下界函数。 3 对下界函数求极值,更新参数分布。 4 迭代计算,直至收敛。 EM算法的流程: 输入:已知数据Y,和未知隐变量Z(随机赋值) 输出: θ \theta θ 1°:给 θ \theta θ 随机赋初值 θ 0 \theta_0 θ0 2°:E步,令 θ n \theta_n θn为第n次已经求得的参数,对 l n P ( y ∣ z ) lnP(y|z) lnP(y∣z)以 P θ n ( z ∣ y ) P_{\theta_n}(z|y) Pθn(z∣y)为概率求期望。 Q ( θ ∣ θ n ) = ∑ z P θ n ( z ∣ y ) l n P ( y ∣ z ) Q(\theta|\theta_n)=\sum_zP_{\theta_n}(z|y)lnP(y|z) Q(θ∣θn)=z∑Pθn(z∣y)lnP(y∣z) 3°:M步,对 Q Q Q函数求偏导,得到极大值,得到使得其获得极大值的 θ \theta θ值。 4°:重复2和3步,直到 ∣ ∣ θ n + 1 − θ n ∣ ∣ ≤ ξ ||\theta_{n+1}-\theta_n || \leq \xi ∣∣θn+1−θn∣∣≤ξ 5°:输出最优模型参数 θ \theta θ EM算法可以保证收敛到一个稳定点,但是不能保证收敛到全局的极大值点,因此是局部的最优算法。当然,如果我们的优化目标是凸的,则EM算法可以保证收敛到全局最大值。 如果我们从算法思想的角度来思考EM算法,我们可以发现我们的算法里已知的是观察数据,未知的是隐含数据和模型参数,在E步,我们所做的事情是固定模型参数的值,优化隐含数据的分布,而在M步,我们所做的事情是固定隐含数据分布,优化模型参数的值。比较下其他的机器学习算法,其实很多算法都有类似的思想。比如SMO算法(支持向量机原理(四)SMO算法原理),坐标轴下降法(Lasso回归算法: 坐标轴下降法与最小角回归法小结), 都使用了类似的思想来求解问题。 三、GMM高斯混合模型指的是多个高斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同分布的情况,或者是同一类分布但是参数不同,或者是不同类型的分布。 GMM中,样本的分类标签是未知的 下图中,明显是两个类别,如果没有GMM,那么只能用一个二维高斯分布来描述图1的数据。 这时候就可以使用GMM了! 如图2,数据在平面上的空间分布和图1一样,这时使用两个二维高斯分布来描述图2中的数据,分别记为
N
(
μ
1
,
Σ
1
)
N(μ 1 ,Σ 1 )
N(μ1,Σ1) 和$N(μ 2 ,Σ 2 )
.
图中的两个椭圆分别是这两个高斯分布的二倍标准差椭圆。可以看到使用两个二维高斯分布来描述图中的数据显然更合理。实际上图中的两个聚类的中的点是通过两个不同的正态分布随机生成而来。如果将两个二维高斯分布
. 图中的两个椭圆分别是这两个高斯分布的二倍标准差椭圆。可以看到使用两个二维高斯分布来描述图中的数据显然更合理。实际上图中的两个聚类的中的点是通过两个不同的正态分布随机生成而来。如果将两个二维高斯分布
.图中的两个椭圆分别是这两个高斯分布的二倍标准差椭圆。可以看到使用两个二维高斯分布来描述图中的数据显然更合理。实际上图中的两个聚类的中的点是通过两个不同的正态分布随机生成而来。如果将两个二维高斯分布N(μ 1 ,Σ 1 )
和
和
和N(μ 2 ,Σ 2 ) $合成一个二维的分布,那么就可以用合成后的分布来描述图2中的所有点。最直观的方法就是对这两个二维高斯分布做线性组合,用线性组合后的分布来描述整个集合中的数据。这就是高斯混合模型(GMM)。 GMM: 设有随机变量X ,则混合高斯模型可以用下式表示: 其中$N(x|μ_ k ,Σ_ k ) 称为混合模型中的第 k 个分量( c o m p o n e n t )。如前面图 2 中的例子,有两个聚类,可以用两个二维高斯分布来表示,那么分量数 称为混合模型中的第k 个分量(component)。如前面图2中的例子,有两个聚类,可以用两个二维高斯分布来表示,那么分量数 称为混合模型中的第k个分量(component)。如前面图2中的例子,有两个聚类,可以用两个二维高斯分布来表示,那么分量数K=2 $. π k π _k πk 是混合系数(mixture coefficient),且满足: ∑ k = 1 K π k = 1 , 0 ≤ π k ≤ 1 \sum_{ k=1}^{ K} π _k =1 ,0\leqπ _k\leq1 k=1∑Kπk=1,0≤πk≤1 π k \pi_k πk相当于每个分量$N(x|μ_ k ,Σ_ k ) $的权重。
|
【本文地址】



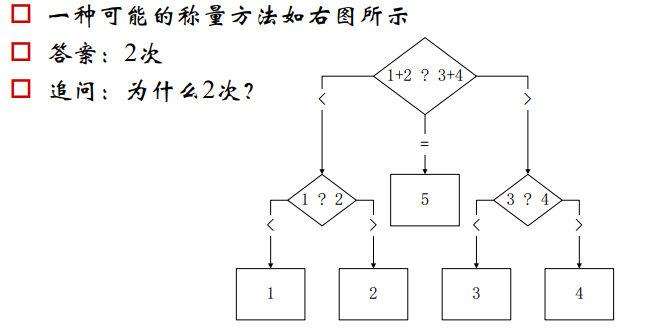

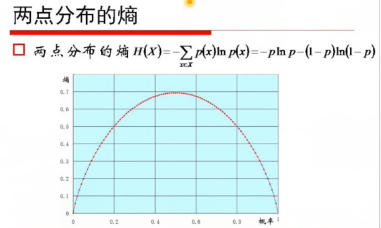
 两点分布的最大熵:
两点分布的最大熵: