核心：爱因斯坦光电效应方程

\begin{equation} h \nu=A+\frac{1}{2} m v_{\mathrm{m}}^2 \end{equation}\\

光子的基本特征

\begin{aligned} & E=m c^2=h v \\ & m=\frac{h v}{c^2}=\frac{h}{c \lambda} \\ & p=m c=\frac{h v}{c}=\frac{h}{\lambda} \end{aligned} \\

普朗克公式尽量记忆M_{B \lambda}(T)=\frac{1}{\lambda^5} \cdot \frac{2 \pi h c^2}{e^{h c / \lambda k T}-1} \\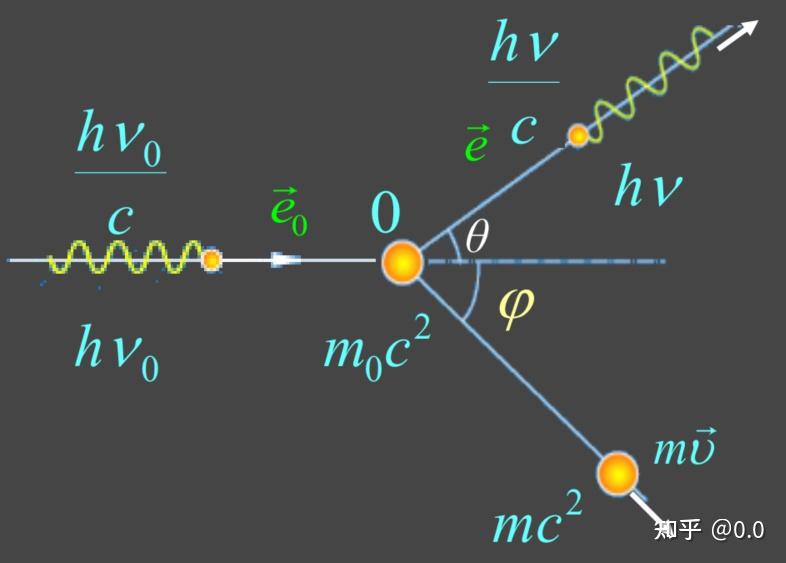

\Delta \lambda=\lambda-\lambda_0=\frac{h}{m_0c}(1-cos\theta)

氢原子只能处于一系列能量不连续的定态。从能量为 E_k 的定态跃迁到能量为 E_n 的定态需要发射或吸收一个频率为 \nu_{kn} 的光子

\nu_{kn}=\frac{\left| E_k-E_n \right|}{h}=\frac{E_1}{hc}(\frac{1}{k^2}-\frac{1}{n^2})=\frac{R_H}{c}(\frac{1}{k^2}-\frac{1}{n^2})\\

① De Broglie假设：一切实物粒子都具有二象性

\lambda=\frac{h}{p}=\frac{h}{m v}=\frac{h}{m_0 v} \sqrt{1-v^2 / c^2} \\ v=\frac{E}{h}=\frac{m c^2}{h}=\frac{m_0 c^2}{h \sqrt{1-v^2 / c^2}} \\ ②不确定关系

动量-坐标不确定关系与 能量-时间不确定关系

\Delta E \Delta t \geq \frac{\hbar}{2}\quad\Delta x \Delta p_x \geq \frac{\hbar}{2}\\

类比机械波的波函数

\begin{aligned} y(x, t) & =A \cos 2 \pi\left(v t-\frac{x}{\lambda}\right) \\ & =A \mathrm{e}^{-i 2 \pi\left(v t-\frac{x}{\lambda}\right)} \end{aligned}\\ 自由粒子的德布罗意波的波函数

\begin{aligned} \Psi(x, t) & =\Psi_0 \mathrm{e}^{-i 2 \pi\left(v t-\frac{x}{\lambda}\right)} \\ & =\Psi_0 \mathrm{e}^{-\frac{i}{\hbar}(E t-p x)}=\Psi_0 \mathrm{e}^{\frac{i}{\hbar} p x} \mathrm{e}^{-\frac{i}{\hbar} E t} \end{aligned}\\ 波函数的统计学解释

\mathrm{d} W=|\Psi(\vec{r}, t)|^2 \mathrm{~d} V=\Psi(\vec{r}, t) \Psi^*(\vec{r}, t) \mathrm{d} V\\ dW 表示粒子 t 时刻在 \vec{r} 空间处单位体积出现的概率,为满足统计意义，必须满足归一化条件和标准化条件

②薛定谔方程的建立

薛定谔方程 \left[-\frac{\hbar^2}{2 m}\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial}{\partial z^2}\right)+V(\vec{r}, t)\right] \Psi(\vec{r}, t)=i \hbar \frac{\partial \Psi(\vec{r}, t)}{\partial t}\\

一维定态薛定谔方程 \frac{\partial^2}{\partial x^2} \Psi(x)+\frac{2 m}{\hbar^2}(E-V) \Psi(x)=0\\上式中， E 为粒子能量， V 描述外力场的势函数（与时间t无关）

若已知m，V，结合初始条件、边界条件、归一化条件，便可由依据一维定态薛定谔方程求解其定态波函数，进而可得粒子在某处或 某空间出现的几率。

由波函数 \Psi_0 \mathrm{e}^{-\frac{i}{\hbar}(E t-p x)}=\Psi_0 \mathrm{e}^{\frac{i}{\hbar} p x} \mathrm{e}^{-\frac{i}{\hbar} E t} 推导一维薛定谔方程，主要依据自由粒子在非相对论条件下的动能 E_k=\frac{p^2}{2m} ，推导其一维含时薛定谔方程

\Psi=\psi_0 e^{-\frac{i}{\hbar}(E t-p x)} \tag{1} （1）式对t求导 \frac{\partial \Psi}{\partial t}=-\frac{i}{\hbar} E \psi_o e^{-\frac{i}{\hbar}(E t-P x)}=-\frac{i}{\hbar} E \Psi \tag{2} 粒子的能量可以写做 E=E_k+E_P=\frac{p^2}{2 m}+E_p \tag{3} （2）带入（3）式得到 i \hbar \frac{\partial \Psi}{\partial t}=\left[\frac{p^2}{2 m}+E_P(x, t)\right] \Psi \tag{4} （1）式对x求二阶偏导 \frac{\partial^2 \Psi}{\partial x^2}=-\frac{p^2}{\hbar^2} \psi_o e^{-\frac{i}{\hbar}(E t-p x)}=-\frac{p^2}{\hbar^2} \Psi \tag{5} 联立（4）（5）得到一维含时薛定谔方程

-\frac{\hbar^2}{2 m} \frac{\partial^2 \Psi}{\partial x^2}+E_P(x, t) \Psi=i \hbar \frac{\partial \Psi}{\partial t} \tag{6} 对于一种更简化的情况，若粒子的势能 E_P 与t无关，仅是坐标t的函数，也就是说，该势场并不是时变场，则（6）式可以写作 -\frac{\hbar^2}{2 m} \frac{\partial^2 \Psi}{\partial x^2}+E_P(x) \Psi=i \hbar \frac{\partial \Psi}{\partial t}\tag{7} 我们进行分离变量，将自由粒子的波函数（1）式拆为仅与x有关和仅与t有关的两项之积 \Psi=\Psi_0 \mathrm{e}^{-\frac{i}{\hbar}(E t-p x)}=\Psi_0 \mathrm{e}^{\frac{i}{\hbar} p x} \mathrm{e}^{-\frac{i}{\hbar} E t} =\psi(x) \Phi(t) \tag{8} 相应的，（7）式的形式也变为 \Phi(t)\left[-\frac{\hbar^2}{2 m} \frac{d^2 \psi(x)}{d x^2}+E_P(x) \psi(x)\right]=\psi(x) i \hbar \frac{d \Phi(t)}{d t} \tag{8} 整理为 \frac{1}{\psi(x)}\left[-\frac{\hbar^2}{2 m} \frac{d^2 \psi(x)}{d x^2}+E_P(x) \psi(x)\right]=\frac{1}{\Phi(t)} i \hbar \frac{d \Phi(t)}{d t} \tag{9} 该式左边的是x的函数，右边是t的函数，等式两边仅在都为常数时才成立，实际上，若设该常数为C， 由\frac{1}{\Phi(t)} i \hbar \frac{d \Phi(t)}{d t} =C 可以解得到

\Phi(t) =\mathrm{e}^{-\frac{i}{\hbar} C t} \tag{10} 而在（8）式中，拆分出的与时间有关的项正是 \Phi(t) =\mathrm{e}^{-\frac{i}{\hbar} E t} \tag{11} 联立（10）（11），不难发现，该常数C就是电子的总能量E，从量纲上也可以验证是如此。这样我们便可以将（8）式写做 一组常微分方程 \left\{\begin{array}{l} \frac{1}{\Phi(t)} \frac{d \Phi(t)}{d t}=\frac{E}{i \hbar} \tag{12} \\ -\frac{\hbar^2}{2 m} \frac{d^2 \psi(x)}{d x^2}+E_P(x) \psi(x)=E \psi(x) \end{array}\right.

其中仅与位置x有关的方程即为一维定态薛定谔方程 \frac{d^2 \psi(x)}{d x^2}+\frac{2 m}{\hbar^2}\left(E-E_P\right) \psi(x)=0 \tag{13} 其中 \psi(x) 为定态波函数。

实际上，当势场为时不变场时，粒子在空间中出现的概率仅与x有关。 我们把这种状态称作定态。\begin{aligned} w=|\Psi(x, t)|^2 & =\psi^*(x) e^{\frac{i}{\hbar} E t} \cdot \psi(x) e^{-\frac{i}{\hbar} E t} \\ & =\psi^*(x) \psi(x)=|\psi(x)|^2 \end{aligned} \\ 若已知m，V，结合初始条件、边界条件、归一化条件，便可由依据一维定态薛定谔方程求解其定态波函数，进而可得粒子在某处或 某空间出现的几率。

薛定谔方程之于量子力学，一如牛顿方程之于经典力学。