VAR(向量自回归)模型 |
您所在的位置:网站首页 › 时间序列模型构建过程 › VAR(向量自回归)模型 |
VAR(向量自回归)模型
|
文章目录
一、简介1.1 内生变量与外生变量1.2 VAR模型概念1.3 VAR模型结构1.4 VAR模型的特点
二、模型的定阶(滞后阶数检验)三、模型的系数估计四、单位根检验五、格兰杰因果检验六、脉冲响应分析七、方差分解
一、简介
1.1 内生变量与外生变量
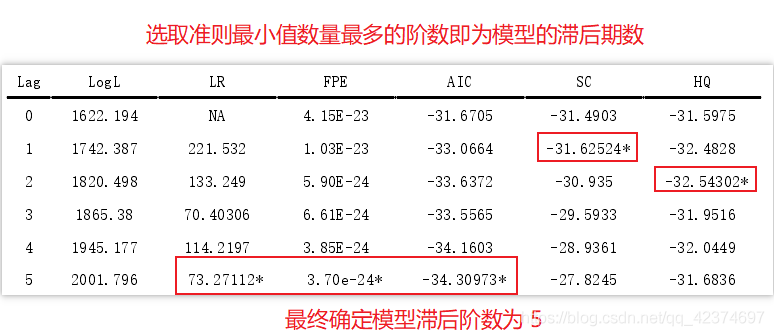
内生变量 内生变量是具有某种概率分布的随机变量,它的参数是联立方程系统估计的元素,是由模型系统决定的,同时也对模型系统产生影响。内生变量–般都是明确经济意义变量。一般情况下,内生变量与随机项相关,即 C o v ( Y i , ε i ) ≠ 0 Cov\left( Y_i,\varepsilon _i \right) \ne 0 Cov(Yi,εi)=0在联立方程模型中,内生变量既作为被解释变量,又可以在不同的方程中作为解释变量。外生变量 外生变量一般是确定性变量,或者是具有临界概率分布的随机变量,其参数不是模型系统研究的元素。外生变量影响系统,但本身不受系统的影响。外生变量一般是经济变量、政策变量、虚拟变量。一般情况下,外生变量与随机项不相关。注意:一个变量是内生变量还是外生变量,由经济理论和经济意义决定,不是从数学形式决定。 1.2 VAR模型概念向量自回归模型,简称VAR模型,是AR 模型的推广,是一种常用的计量经济模型。在一定的条件下,多元MA和ARMA模型也可转化成VAR模型。 VAR模型是用模型中所有当期变量对所有变量的若干滞后变量进行回归。 即 向量自回归模型把系统中每-一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型,从而实现了将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型。 VAR模型常用于预测相互联系的时间序列系统以及分析随机扰动对变量系统的动态影响,主要应用于宏观经济学。是处理多个相关经济指标的分析与预测中最容易操作的模型之一。 由于向量自回归模型把每个内生变量作为系统中所有内生变量滞后值的函数来构造模型,从而避开了结构建模方法中需要对系统每个内生变量关于所有内生变量滞后值的建模问题。 1.3 VAR模型结构单变量的时间序列的分析模式可以推广到多变量时间序列,建立向量自回归模型。向量自回归模型通常用于描述多变量时间序列之间的变动关系,不需要经济理论作为基础,从数据出发建立模型,是一种非结构化的模型。 非限制性向量自回归模型的一般表达式如下: 模型的基本形式是弱平稳过程的自回归表达式,描述的是在同一样本期间内的若干变量可以作为它们过去值的线性函数。 Y t = Φ 0 + Φ 1 Y t − 1 + ⋯ + Φ p Y t − p + B X t + ε t , t = 1 , 2 , ⋯ , T Y_t=\varPhi _0+\varPhi _1Y_{t-1}+\cdots +\varPhi _pY_{t-p}+BX_t+\varepsilon _t\ \text{,\ }t=1,2,\cdots ,T Yt=Φ0+Φ1Yt−1+⋯+ΦpYt−p+BXt+εt , t=1,2,⋯,T 其中 Y t = ( y 1 t y 2 t ⋮ y k t ) , ε t = ( ε 1 t ε 2 t ⋮ ε k t ) , Φ 0 = ( ϕ 10 ϕ 20 ⋮ ϕ k 0 ) Y_t=\left( \begin{array}{c} y_{1t}\\ y_{2t}\\ \vdots\\ y_{kt}\\ \end{array} \right) \text{,}\varepsilon _t=\left( \begin{array}{c} \varepsilon _{1t}\\ \varepsilon _{2t}\\ \vdots\\ \varepsilon _{kt}\\ \end{array} \right) \text{,}\varPhi _0=\left( \begin{array}{c} \phi _{10}\\ \phi _{20}\\ \vdots\\ \phi _{k0}\\ \end{array} \right) Yt=⎝⎜⎜⎜⎛y1ty2t⋮ykt⎠⎟⎟⎟⎞,εt=⎝⎜⎜⎜⎛ε1tε2t⋮εkt⎠⎟⎟⎟⎞,Φ0=⎝⎜⎜⎜⎛ϕ10ϕ20⋮ϕk0⎠⎟⎟⎟⎞ Φ i = ( ϕ 11 ( i ) ϕ 12 ( i ) ⋯ ϕ 1 k ( i ) ϕ 21 ( i ) ϕ 22 ( i ) ⋯ ϕ 2 k ( i ) ⋮ ⋮ ⋱ ⋮ ϕ k 1 ( i ) ϕ k 2 ( i ) ⋯ ϕ k k ( i ) ) , i = 1 , 2 , ⋯ , p \varPhi _i=\left( \begin{matrix} \phi _{11}\left( i \right)& \phi _{12}\left( i \right)& \cdots& \phi _{1k}\left( i \right)\\ \phi _{21}\left( i \right)& \phi _{22}\left( i \right)& \cdots& \phi _{2k}\left( i \right)\\ \vdots& \vdots& \ddots& \vdots\\ \phi _{k1}\left( i \right)& \phi _{k2}\left( i \right)& \cdots& \phi _{kk}\left( i \right)\\ \end{matrix} \right) \,\,\text{,\,\,}i=1,2,\cdots ,p Φi=⎝⎜⎜⎜⎛ϕ11(i)ϕ21(i)⋮ϕk1(i)ϕ12(i)ϕ22(i)⋮ϕk2(i)⋯⋯⋱⋯ϕ1k(i)ϕ2k(i)⋮ϕkk(i)⎠⎟⎟⎟⎞,i=1,2,⋯,p Y t Y_t Yt 表示 k 维内生变量列向量 Y t − i , i = 1 , 2 , ⋯ , p Y_{t-i}\text{,}i=1,2,\cdots ,p Yt−i,i=1,2,⋯,p 为滞后的内生变量 X t X_t Xt 表示 d 维外生变量列向量,它可以是常数变量、线性趋势项或者其他非随机变量p 是滞后阶数T 为样本数目 Φ i \varPhi _i Φi 即 Φ 1 , Φ 2 ⋯ , Φ p \varPhi _1,\varPhi _2\cdots ,\varPhi _p Φ1,Φ2⋯,Φp 为 k × k k\times k k×k 维的待估矩阵B 为 k × d k\times d k×d 维的待估矩阵 ε t ∼ N ( 0 , Σ ) \varepsilon _t\sim N\left( 0,\varSigma \right) εt∼N(0,Σ) 为 k 维白噪声向量,它们相互之间可以同期相关,但不与自己的滞后项相关(诸 ε t \varepsilon _t εt 独立同分布,而 ε t \varepsilon _t εt 中的分量不要求相互独立),也不与上式中右边的变量相关。 Σ \varSigma Σ 是 ε t \varepsilon _t εt 的协方差矩阵, 是一个 k × k k\times k k×k 的正定矩阵。.比如 1 维 p 阶 向量自回归模型 { y 1 t = ϕ 10 + ϕ 11 ( 1 ) y 1 , t − 1 + ϕ 12 ( 1 ) y 2 , t − 1 + ⋯ + ϕ 1 n ( 1 ) y n , t − 1 + ϕ 11 ( 2 ) y 1 , t − 2 + ϕ 12 ( 2 ) y 2 , t − 2 + ⋯ + ϕ 1 n ( 2 ) y n , t − 2 + ⋯ + ϕ 11 ( p ) y 1 , t − p + ϕ 12 ( p ) y 2 , t − p + ⋯ + ϕ 1 n ( p ) y n , t − p + ε t \left\{ \begin{array}{l} y_{1t}=\phi _{10}+\phi _{11}\left( 1 \right) y_{1,t-1}+\phi _{12}\left( 1 \right) y_{2,t-1}+\cdots +\phi _{1n}\left( 1 \right) y_{n,t-1}\\ \ \ \ \ \ \ \ \ +\phi _{11}\left( 2 \right) y_{1,t-2}+\phi _{12}\left( 2 \right) y_{2,t-2}+\cdots +\phi _{1n}\left( 2 \right) y_{n,t-2}\\ \ \ \ \ \ \ \ \ +\cdots\\ \ \ \ \ \ \ \ \ +\phi _{11}\left( p \right) y_{1,t-p}+\phi _{12}\left( p \right) y_{2,t-p}+\cdots +\phi _{1n}\left( p \right) y_{n,t-p}+\varepsilon _t\\ \end{array} \right. ⎩⎪⎪⎨⎪⎪⎧y1t=ϕ10+ϕ11(1)y1,t−1+ϕ12(1)y2,t−1+⋯+ϕ1n(1)yn,t−1 +ϕ11(2)y1,t−2+ϕ12(2)y2,t−2+⋯+ϕ1n(2)yn,t−2 +⋯ +ϕ11(p)y1,t−p+ϕ12(p)y2,t−p+⋯+ϕ1n(p)yn,t−p+εt 不含常数项或线性趋势项的向量自回归模型表达式为: Y t = Φ 1 Y t − 1 + ⋯ + Φ p Y t − p + ε t , t = 1 , 2 , ⋯ , T Y_t=\varPhi _1Y_{t-1}+\cdots +\varPhi _pY_{t-p}+\varepsilon _t\ \text{,\ }t=1,2,\cdots ,T Yt=Φ1Yt−1+⋯+ΦpYt−p+εt , t=1,2,⋯,T 1.4 VAR模型的特点 不以严格的经济理论为依据。在建模过程中只需明确两件事:①共有哪些变量是相互有关系的,把有关系的变量包括在VAR模型中;②确定滞后期 p。使模型能反映出变量间相互影响的绝大部分。VAR模型对参数不施加零约束。(对无显着性的参数估计值并不从模型中剔除,不分析回归参数的经济意义。)VAR模型的解释变量中不包括任何当期变量,所有与联立方程模型有关的问题在VAR模型中都不存在(主要是参数估计量的非一致性问题)。VAR模型的另一个特点是有相当多的参数需要估计。比如一个VAR模型含有三个变量,最大滞后期 p=3,则有27个参数需要估计。当样本容量较小时,多数参数的估计量误差较大。无约束VAR模型的应用之一是预测。由于在VAR模型中每个方程的右侧都不含有当期变量,这种模型用于样本外一期预测的优点是不必对解释变量在预测期内的取值做任何预测。用VAR模型做样本外近期预测非常准确。做样本外长期预测时,则只能预测出变动的趋势,而对短期波动预测不理想。 二、模型的定阶(滞后阶数检验)滞后阶数检验需要考虑两个问题: 第一,如果滞后阶数 p 比较小,那么随机误差项会出现自相关的问题;第二,在实际应用中,通常希望滞后阶数 p 足够大,进而能够更好的体现所构造的模型的动态特征,但是如果滞后阶数 p 过大时,那么模型所需要估计的参数就越多,将存在自由度太小的问题,如果没有足够多的样本数量,就会造成所需要估计参数不能有效的计算出来。所以,在做滞后阶数检验之前,需要把各种因素都考虑在内,这样才能保证检验结果是有效的。 有两种方法可以做滞后阶数检验: 第–种方法,分析各种准则,最后确定滞后阶数,AIC准则、SC准则、HQ准则、LogL准则、最终预测误差(FPE);.第二种方法,分析似然比(LR),这种方法不会出现第一-种方法的无效结果。第一种方法被学者们用的最多。.第一种方法中的五个指标在各个阶数的估计值,选取五个检验准则最小值数量最多的阶数即为模型的滞后期数。 比如
对于向量自回归模型系统中的每一个方程都可以采用OLS(最小二乘估计)方法进行估计,同时估计量具有一致性和无偏性。 一个 k 维 p 阶向量自回归模型中,各方程中所有解释变量的滞后期是相同的,都为滞后 p 期,因此共估计得到 p × k 2 + k p\times k^2+k p×k2+k 个系数。 四、单位根检验时间序列平稳性是指–组数列的统计值与时间无关,不会随时间推移而变化,它通常是以因果关系为基础的数学模型的假设条件。 如果时间序列 y t y_t yt 是一组平稳序列,那么经过计算分析得到其均值 E ( y t ) E\left( y_t \right) E(yt) 不随时间变化而变化,其方差 V a r ( y t ) Var\left( y_t \right) Var(yt) 也不受时间的影响。如果时间序列 y t y_t yt 不是一组平稳序列,那么它的均值和方差都会受到时间t影响,随之改变。在VAR模型中,必须保证时间序列稳定。如果不能保证时间序列稳定,那么会导致两种结果: 第一,向量自回归系数的估计值是负数,做完 t 检验后,得到的结果是无效的; 第二,两个独立变量的相关关系或者回归关系是假的,使得模型的结果无效。 (1)DF 检验 DF 检验只适用于一阶自回归过程的平稳性检验 在一阶自回归序列中, y t = ϕ 1 y t − 1 + ε t , ε t ∼ N ( 0 , σ ε 2 ) y_t=\phi _1y_{t-1}+\varepsilon _t\ ,\ \varepsilon _t\sim N\left( 0,\sigma _{\varepsilon}^2 \right) yt=ϕ1yt−1+εt , εt∼N(0,σε2) 该序列的特征方程为: λ − ϕ 1 = 0 \lambda -\phi _1=0 λ−ϕ1=0 特征根为: λ = ϕ 1 \lambda =\phi _1 λ=ϕ1 当特征根在单位圆内时: ∣ ϕ 1 ∣ < 1 \left| \phi _1 \right|y2t=ϕ20+ϕ21(1)y1,t−1+ϕ21(2)y1,t−2+⋯+ϕ21(p)y1,t−p +ϕ22(1)y2,t−1+ϕ22(2)y2,t−2+⋯+ϕ22(p)y2,t−p+εt 可以写成 ∣ [ y 1 t y 2 t ] = [ ϕ 10 ϕ 20 ] + [ ϕ 11 ( 1 ) ϕ 12 ( 1 ) ϕ 21 ( 1 ) ϕ 22 ( 1 ) ] [ y 1 , t − 1 y 2 , t − 1 ] + [ ϕ 11 ( 2 ) ϕ 12 ( 2 ) ϕ 21 ( 2 ) ϕ 22 ( 2 ) ] [ y 1 , t − 2 y 2 , t − 2 ] + ⋯ + [ ϕ 11 ( p ) ϕ 12 ( p ) ϕ 21 ( p ) ϕ 22 ( p ) ] [ y 1 , t − p y 2 , t − p ] + [ ε 1 t ε 2 t ] \left| \begin{array}{l} \left[ \begin{array}{c} y_{1t}\\ y_{2t}\\ \end{array} \right] =\left[ \begin{array}{c} \phi _{10}\\ \phi _{20}\\ \end{array} \right] +\left[ \begin{matrix} \phi _{11}\left( 1 \right)& \phi _{12}\left( 1 \right)\\ \phi _{21}\left( 1 \right)& \phi _{22}\left( 1 \right)\\ \end{matrix} \right] \left[ \begin{array}{c} y_{1,t-1}\\ y_{2,t-1}\\ \end{array} \right] +\left[ \begin{matrix} \phi _{11}\left( 2 \right)& \phi _{12}\left( 2 \right)\\ \phi _{21}\left( 2 \right)& \phi _{22}\left( 2 \right)\\ \end{matrix} \right] \left[ \begin{array}{c} y_{1,t-2}\\ y_{2,t-2}\\ \end{array} \right]\\ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\cdots +\left[ \begin{matrix} \phi _{11}\left( p \right)& \phi _{12}\left( p \right)\\ \phi _{21}\left( p \right)& \phi _{22}\left( p \right)\\ \end{matrix} \right] \left[ \begin{array}{c} y_{1,t-p}\\ y_{2,t-p}\\ \end{array} \right] +\left[ \begin{array}{c} \varepsilon _{1t}\\ \varepsilon _{2t}\\ \end{array} \right]\\ \end{array} \right. ∣∣∣∣∣∣∣∣∣∣[y1ty2t]=[ϕ10ϕ20]+[ϕ11(1)ϕ21(1)ϕ12(1)ϕ22(1)][y1,t−1y2,t−1]+[ϕ11(2)ϕ21(2)ϕ12(2)ϕ22(2)][y1,t−2y2,t−2] +⋯+[ϕ11(p)ϕ21(p)ϕ12(p)ϕ22(p)][y1,t−py2,t−p]+[ε1tε2t] 检验原假设: H 0 : y 2 t 不是 y 1 t 的格兰杰原因 H_0:\ y_{2t}\text{不是}y_{1t}\text{的格兰杰原因} H0: y2t不是y1t的格兰杰原因 则通过F检验来检验联合假设 ϕ 12 ( 1 ) = ϕ 12 ( 2 ) = ⋯ = ϕ 12 ( p ) = 0 \phi _{12}\left( 1 \right) =\phi _{12}\left( 2 \right) =\cdots =\phi _{12}\left( p \right) =0 ϕ12(1)=ϕ12(2)=⋯=ϕ12(p)=0 若检验结果拒绝原假设,即拒绝 y 2 t y_{2t} y2t 不是 y 1 t y_{1t} y1t 的格兰杰原因,则通常称 y 2 t y_{2t} y2t 是 y 1 t y_{1t} y1t 的格兰杰原因。 由于格兰杰因果关系检验是在向量自回归模型的基础上进行的,因此向量自回归模型本身的合理性对格兰杰因果关系检验的结果也是非常重要的。例如,向量自回归模型本身应当具有恰当的滞后期。 六、脉冲响应分析在VAR模型中,脉冲响应分析的作用是可以分析某个变量对另一个变量的影响时间和幅度。研究当扰动项发生变化时,对整个模型系统产生的影响,用来描述一个变量的变动怎样影响模型其他所有的变量。 如果时间序列是稳定的,虽然前几期受到外部冲击的影响,该变量会处于一个变化的状态,但经过一段时间,最终会处于-一个平稳的状态。 由于向量自回归模型表达式中所需要估计的参数非常多,并且一个系数只能反应局部关系。 也就是,VAR模型中的各个等式中的系数并不是研究者最终关注的对象,对模型表达式中的系数的研究意义并不大。但是如果考虑一个扰动项变动,或者受到一个干扰或冲击,各个变量之间的动态关系,也就是系统的动态反应,是具有–定意义的。 脉冲响应函数 在参数估计量的评价标准中,一般包含无偏性、有效性、相合性和一致性,而VAR模型参数的普通最小二乘法估计量只具有–致性,因此要解释复杂的经济问题,单个参数估计值是很难完成的。 一个有效的对VAR模型进行分析的方法就是脉冲响应函数。 脉冲响应函数研究的是随机干扰项遭受冲击后内生变量的反应,用来描述对随机干扰项施加一一个冲击后对内生变量的当期值和未来值造成的影响。 在实际的应用中,由于VAR模型是一种非理论性的模型,因此在对VAR模型的分析中,很少研究一个变量的变化对另-一个变量的影响,而是专注于当一个随机误差项变化时(对随机误差项施加冲击),对系统的动态影响。 七、方差分解在VAR模型中,得到了某个变量对另一个变量的解释度后,能够分析出该变量的重要性。变量会产生一些随机误差项,这些随机误差项都包含着重要的信息,方差分解的结果能够把这些信息全部说明出来。方差分解的作用非常大,这个过程的作用是能够分析某个变量对另-一个变量的解释度。 如果说脉冲响应函数是来描述数学模型中的任一内生变量的正交冲击对其他变量造成的影响,那么方差分解就是分析各个内生变量的正交冲击对目标内生变量冲击的贡献比例,进而判断分析各个变量的重要性。 参考: 《浅析中国对美贸易额的影响因素》_张康琦 《基于VAR模型的GDP和CPI对居民生活水平的影响分析》_陈小龙 《向量自回归模型扰动分布的光滑检验及其应用》_钟嫕姝 |
【本文地址】
今日新闻 |
推荐新闻 |