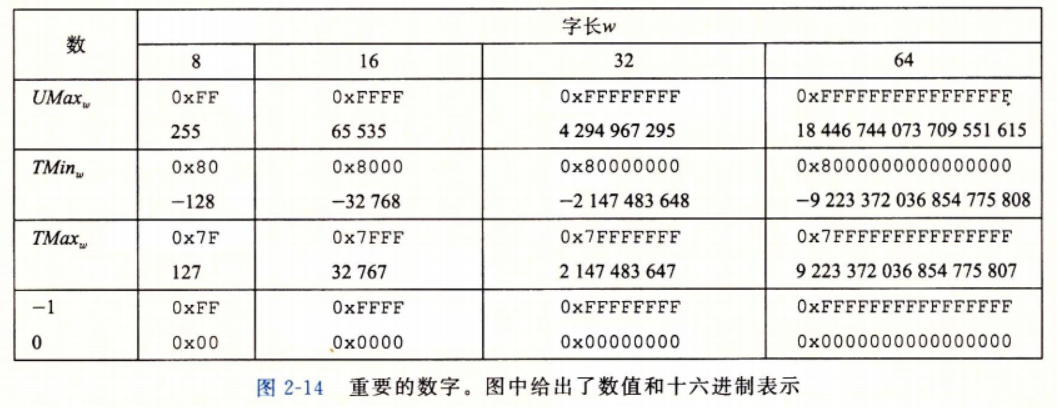
通常来说，用位来编码整数有两种不同的方式

无符号数只能表示非负数，当所有位全为0是表示的值为0，其他情况均表示的是正数

其定义如下：

对向量 x → = [ x w − 1 , x w − 2 , . . . , x 0 ] \overrightarrow{x}=[x_{w-1},x_{w-2},...,x_{0}] x =[xw−1​,xw−2​,...,x0​]而言，其无符号数编码的值为： B 2 U w ( x → ) ≐ ∑ i = 0 w − 1 x i w i B2U_w(\overrightarrow{x})\doteq \sum^{w-1}_{i=0}{x_iw^i} B2Uw​(x )≐i=0∑w−1​xi​wi

用函数 B 2 U w B2U_w B2Uw​(Binary to Unsigned的缩写，长度为 w)来表示二进制转无符号数

例子： B 2 U 4 ( [ 0001 ] ) = 0   ⋅ 2 3 + 0   ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 0 + 0 + 0 + 1 = 1 B 2 U 4 ( [ 0101 ] ) = 0   ⋅ 2 3 + 1   ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 0 + 4 + 0 + 1 = 5 B 2 U 4 ( [ 1011 ] ) = 1   ⋅ 2 3 + 0   ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 8 + 0 + 2 + 1 = 11 B 2 U 4 ( [ 1111 ] ) = 1   ⋅ 2 3 + 1   ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 8 + 4 + 1 + 1 = 15 \begin{aligned} &B2U_4([0001])=0\ \cdot 2^3+0\ \cdot 2^2+0\cdot 2^1+1\cdot 2^0=0+0+0+1=1 \\ &B2U_4([0101])=0\ \cdot 2^3+1\ \cdot 2^2+0\cdot 2^1+1\cdot 2^0=0+4+0+1=5 \\ &B2U_4([1011])=1\ \cdot 2^3+0\ \cdot 2^2+1\cdot 2^1+1\cdot 2^0=8+0+2+1=11 \\ &B2U_4([1111])=1\ \cdot 2^3+1\ \cdot 2^2+1\cdot 2^1+1\cdot 2^0=8+4+1+1=15 \\ \end{aligned} ​B2U4​([0001])=0 ⋅23+0 ⋅22+0⋅21+1⋅20=0+0+0+1=1B2U4​([0101])=0 ⋅23+1 ⋅22+0⋅21+1⋅20=0+4+0+1=5B2U4​([1011])=1 ⋅23+0 ⋅22+1⋅21+1⋅20=8+0+2+1=11B2U4​([1111])=1 ⋅23+1 ⋅22+1⋅21+1⋅20=8+4+1+1=15​

最常见的有符号数的计算机表示方式就是补码(two 's complement)形式

在这个定义中，将字的最好有效位解释为负权（negative weight）

用函数 B 2 T w B2T_w B2Tw​(Binary to Two 's complement的缩写，长度为 w)来表示二进制转补码

补码的定义如下

对向量 x → = [ x w − 1 , x w − 2 , . . . , x 0 ] \overrightarrow{x}=[x_{w-1},x_{w-2},...,x_{0}] x =[xw−1​,xw−2​,...,x0​]而言，其补码编码的值为： B 2 T w ( x → ) ≐ − x w − 1 2 w − 1 + ∑ i = 0 w − 1 x i w i B2T_w(\overrightarrow{x})\doteq -x_{w-1}2^{w-1}+ \sum^{w-1}_{i=0}{x_iw^i} B2Tw​(x )≐−xw−1​2w−1+i=0∑w−1​xi​wi

最高有效位 x w − 1 x_{w-1} xw−1​也称为符号位，它的“权重”为 − 2 w − 1 -2^{w-1} −2w−1，是无符号表示中权重的负数。 符号位被设置为1时， 表示值为负， 而当设置为0时， 值为非负。

例子（请与上面的无符号数的例子对照看）： B 2 T 4 ( [ 0001 ] ) = − 0   ⋅ 2 3 + 0   ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 0 + 0 + 0 + 1 = 1 B 2 T 4 ( [ 0101 ] ) = − 0   ⋅ 2 3 + 1   ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 0 + 4 + 0 + 1 = 5 B 2 T 4 ( [ 1011 ] ) = − 1   ⋅ 2 3 + 0   ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = − 8 + 0 + 2 + 1 = − 5 B 2 T 4 ( [ 1111 ] ) = − 1   ⋅ 2 3 + 1   ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = − 8 + 4 + 2 + 1 = − 1 \begin{aligned} &B2T_4([0001])=-0\ \cdot 2^3+0\ \cdot 2^2+0\cdot 2^1+1\cdot 2^0=0+0+0+1=1 \\ &B2T_4([0101])=-0\ \cdot 2^3+1\ \cdot 2^2+0\cdot 2^1+1\cdot 2^0=0+4+0+1=5 \\ &B2T_4([1011])=-1\ \cdot 2^3+0\ \cdot 2^2+1\cdot 2^1+1\cdot 2^0=-8+0+2+1=-5 \\ &B2T_4([1111])=-1\ \cdot 2^3+1\ \cdot 2^2+1\cdot 2^1+1\cdot 2^0=-8+4+2+1=-1 \\ \end{aligned} ​B2T4​([0001])=−0 ⋅23+0 ⋅22+0⋅21+1⋅20=0+0+0+1=1B2T4​([0101])=−0 ⋅23+1 ⋅22+0⋅21+1⋅20=0+4+0+1=5B2T4​([1011])=−1 ⋅23+0 ⋅22+1⋅21+1⋅20=−8+0+2+1=−5B2T4​([1111])=−1 ⋅23+1 ⋅22+1⋅21+1⋅20=−8+4+2+1=−1​

补码的取值范围：

假设编码字长为w

补码所能表示的最小值为 [ 10...0 ] [10...0] [10...0]（也就是除了最高位符号位为1外其他全为0），其表示的值为 T M i n w = − 2 w − 1 TMin_w=-2^{w-1} TMinw​=−2w−1，

补码所能表示的最大值是 [ 01...1 ] [01...1] [01...1]（也就是除了最高位符号位为0外其他全为1），其表示的值为 T M a x w = ∑ i = 0 w − 2 2 i = 2 w − 1 − 1 TMax_w=\sum^{w-2}_{i=0}{2^i}=2^{w-1}-1 TMaxw​=∑i=0w−2​2i=2w−1−1

故补码所能表示的范围为 [ T M i n w , T M a x w ] = [ − 2 w − 1 , 2 w − 1 − 1 ] [TMin_w,TMax_w]=[-2^{w-1},2^{w-1}-1] [TMinw​,TMaxw​]=[−2w−1,2w−1−1]

由上式可以看出来 ∣ T M i n w ∣ = ∣ T M a x w ∣ + 1 |TMin_w|=|TMax_w|+1 ∣TMinw​∣=∣TMaxw​∣+1，即负数表示范围比正数的表示范围要大，也就是说 T M i n TMin TMin没有与之对应的正数，之所以有这样的不对成性，是因为一半的位模式（符号位设置为1的数）表示负数，另一半（符号位设置为0的数）表示非负数。因为0是非负数，也就是意味着能表示的整数比负数少一个

另外还有一点需要注意的是，最大的无符号数刚好比补码的最大值的两倍大一点，也就是 U M a x w = 2 T M a x w + 1 UMax_w=2TMax_w+1 UMaxw​=2TMaxw​+1，这点可以通过很简单的运算得到，可以对照下图自行推导一下

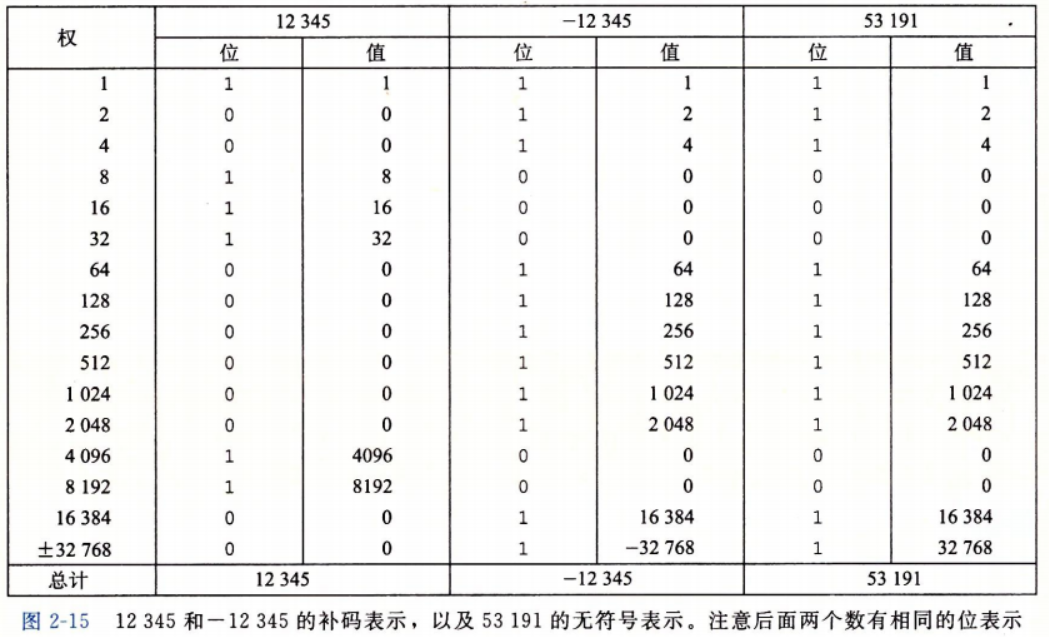
例子：

以编码字长为4为例 T M i n 4 = B 2 T 4 ( [ 1000 ] ) = − 2 3 = − 8 T M a x 4 = B 2 T 4 ( [ 0111 ] ) = 2 2 + 2 1 + 2 0 = 4 + 2 + 1 = 7 \begin{aligned} &TMin_4=B2T_4([1000])=-2^3=-8\\ &TMax_4=B2T_4([0111])=2^2+2^1+2^0=4+2+1=7 \end{aligned} ​TMin4​=B2T4​([1000])=−23=−8TMax4​=B2T4​([0111])=22+21+20=4+2+1=7​

补充：

在大学计算机基础教程中也会有如下说法

有符号数共有三种标准的表示方式：原码、反码、补码

原码：使用最高位表示符号位（0表示正，1表示负），其他位表示数据的值

举例：

反码：反码是在原码的基础上通过一定的规则转换得到的另一种无符号数表示的方式，其规则如下

补码：补码是在反码的基础上通过一定的规则转化得到的另一种无符号数表示的方式，其规则如下

总结：

举例： [ + 45 ] 原 = 0010 , 1101      [ − 45 ] 原 = 1010 , 1101 [ + 45 ] 反 = 0010 , 1101      [ − 45 ] 反 = 1101 , 0010 [ + 45 ] 补 = 0010 , 1101      [ − 45 ] 补 = 1101 , 0011 [+45]原=0010,1101\ \ \ \ [-45]原=1010,1101 \\ [+45]反=0010,1101\ \ \ \ [-45]反=1101,0010 \\ [+45]补=0010,1101\ \ \ \ [-45]补=1101,0011 [+45]原=0010,1101    [−45]原=1010,1101[+45]反=0010,1101    [−45]反=1101,0010[+45]补=0010,1101    [−45]补=1101,0011

对于大多数C语言的实现来说，对这个问题的回答都是从位级角度来看的

比如说，考虑如下代码：

在一台采用补码的机器上，上述代码会产生如下输出：

v = 12345 ， m v = − 12345 ， u v = 53191 v = 12345，mv = -12345，uv = 53191 v=12345，mv=−12345，uv=53191

将其转换为二进制表示如下图，我们可以看到在将一个数转换为其相反数表示形式时，其位模式发生了改变，而在进行强制类型转换的时候，位模式并没有发生变化，只是改变了解释这些位的方式，从下图中也可以看到， − 12345 -12345 −12345的16位补码表示与 53191 53191 53191的16位无符号表示是完全一样的。将short强制类型转换为unsigned short改变数值，但不改变位表示。

再来看一个例子：

同样的，在一台采用补码的机器上，上述代码会产生如下输出

u = 4294967295 u , t u = − 1 u = 4294967295u, tu = -1 u=4294967295u,tu=−1

从图2-14（在上面）可以看出，对于32位字长来说，无符号形式的 4294967295 4294967295 4294967295和补码形式的 − 1 -1 −1的位模式是一模一样的。

同样的，将unsigned强制类型转换位int，底层的位表示不变

对于大多数C语言的实现，处理同样字长的有符号数和无符号数之间相互转换的一般规则是：数字可能会改变，但是位模式不会变

T 2 U w T2U_w T2Uw​表示将w位的补码转换为无符号数， U 2 T w U2T_w U2Tw​表示将w位的无符号数转换为补码

从第一个例子可以看出来 T 2 U 16 ( − 12345 ) = 53191 T2U_{16}(-12345)=53191 T2U16​(−12345)=53191，并且 U 2 T 16 ( 53191 ) = − 12345 U2T_{16}(53191)=-12345 U2T16​(53191)=−12345。也就是说，十六进制表示写作 0 x C F C 7 0xCFC7 0xCFC7的16位位模式既是-12345的补码表示，又是53191的无符号表示。同时注意 12345 + 53191 = 65363 = 2 16 12345+53191=65363=2^{16} 12345+53191=65363=216。类似地，对于第二个例子来说，也有如下关系 T 2 U 32 ( − 1 ) = 4294967295 T2U_{32}(-1)=4294967295 T2U32​(−1)=4294967295，并且 U 2 T 32 ( 4294967295 ) = − 1 U2T_{32}(4294967295)=-1 U2T32​(4294967295)=−1。也就是说，无符号表示中的 U M a x UMax UMax有着和补码表示的-1相同的位模式，我们在这两个数之间也能看到这种关系： 1 + U M a x w = 2 w 1+UMax_w=2^w 1+UMaxw​=2w。这个属性可以推广到给定位模式的两个数值（补码和无符号数）之间的关系

通过上述这些例子，我们可以得到如下关系：

补码转换为无符号数的规则：

对满足 T M i n w ≤ x ≤ T M a x w TMin_w\le x \le TMax_w TMinw​≤x≤TMaxw​的 x x x有： T 2 U w ( x ) = { x + 2 w , x