05 高等数学专题 |
您所在的位置:网站首页 › 无穷级数视频讲解 › 05 高等数学专题 |
05 高等数学专题
|
一、数列{an}
定义:数列通项极限存在(即趋于某个常数),则称数列收敛 (反之数列收敛,则数列通项的极限存在) 单调有界准则:数列是单调有界数列,,则极限存在数列收敛(反之数列收敛,则数列有界,性质:有界性) 注: 数列极限存在与数列有界不等价:极限存在则一定有界 有界且单调则极限存在,其他不一定,如{sinn}不收敛但有界 二、级数 ∑ a n \sum an ∑an、前n项和数列{Sn}、数列{an}:正项级数部分和数列{Sn}有界(内含单调性)=> 部分和数列{Sn}收敛=> 即级数 ∑ a n \sum an ∑an前n项和极限存在,级数收敛=> 通项an极限为0,即数列{an}收敛=> 数列{an}有界 举例: 没有变量n的常数项级数都是收敛数列,但不是收敛级数 {1/n}数列是收敛的数列,但是{1/n}级数不是收敛的级数。 定义:一个级数n项和极限存在,则这个级数收敛(反之级数收敛,则级数的n项和极限存在) 级数收敛的必要条件:通项的极限趋向于0 级数收敛分类:条件收敛和绝对收敛 级数收敛的性质:同乘不为0的常数、两个收敛级数、加上有限项、任意加括号 3.2 常数项级数 判断常数项级数收敛性 1.定义法:前n项和的极限存在对应幂级数和函数函数值 幂级数的x取收敛域中的数,幂级数变成一个常数项级数,常数项级数的 前n项和的极限=和函数在该点的函数值 幂级数取收敛域之外的数时,幂级数变成一个常数项级数,常数项级数不收敛 x0点收敛,比x0小的点绝对收敛 x0点发散,比x0大的点发散 重要结论:条件收敛的点代表着收敛与不收敛的分割线,确定收敛半径 1.幂级数乘以系数k 收敛域不变,和函数乘以系数k 2.两个幂级数相加(-Ra,Ra)(-Rb,Rb) 收敛半径取两者之间更小的,和函数相加 3.两个幂级数相乘(-Ra,Ra)(-Rb,Rb) 收敛半径取两者之间更小的,和函数相乘 3.逐项求导 收敛半径不变,端点的敛散性可能发散变化,和函数求导 4.逐项积分 收敛半径不变,端点的敛散性可能发散变化,和函数积分 1.先求收敛域 好像是正项级数的比值判别法 R = lim n → ∞ ∣ a n a n + 1 ∣ R=\lim\limits_{n\rightarrow\infty}|\frac{a_n}{a_{n+1}}| R=n→∞lim∣an+1an∣ R是收敛半径,(-R,R)是收敛区间 判断x=-R和x=R上的收敛性来确定收敛域 2.再求和函数(利用常用的级数公式) 如: 1 + x + x 2 + . . . + x n = ∑ 0 ∞ x n = 1 1 − x 1+x+x^2+...+x^n=\sum_0^\infty x^n=\frac{1}{1-x} 1+x+x2+...+xn=∑0∞xn=1−x1 收敛域(-1,1 ) 3.与公式对照,确定使用那个展开式公式 关于求导或积分的具体操作: 若幂级数求导过后累加的n起始值发生了变化,若任然化成和原来一样an可能变成an+1,所以求导之后和原来级数也就不同了 幂级数积分时下标是不变的 幂级数求导之后下标变化与否要判断原级数的首项求导过后还剩不剩东西下来 怎么操作不明显的时候,可以提取或增加x 函数的幂级数展开(常用展开式公式)1 1 − x = 1 + x + x 2 + . . . + x n = ∑ 0 ∞ x n 收 敛 域 ( − 1 , 1 ) \frac{1}{1-x}=1+x+x^2+...+x^n=\sum_0^\infty x^n \\收敛域(-1,1 ) 1−x1=1+x+x2+...+xn=0∑∞xn收敛域(−1,1) 1 1 + x = 1 − x + x 2 + . . . + ( − 1 ) n x n = ∑ 0 ∞ ( − 1 ) n x n 收 敛 域 ( − 1 , 1 ) \frac{1}{1+x}=1-x+x^2+...+(-1)^nx^n=\sum_0^\infty (-1)^nx^n\\ 收敛域(-1,1 ) 1+x1=1−x+x2+...+(−1)nxn=0∑∞(−1)nxn收敛域(−1,1)
?展开式有收敛域,不是说在某个去心领域内可以展开成泰勒级数吗,那为什么收敛会是R |
【本文地址】
今日新闻 |
推荐新闻 |


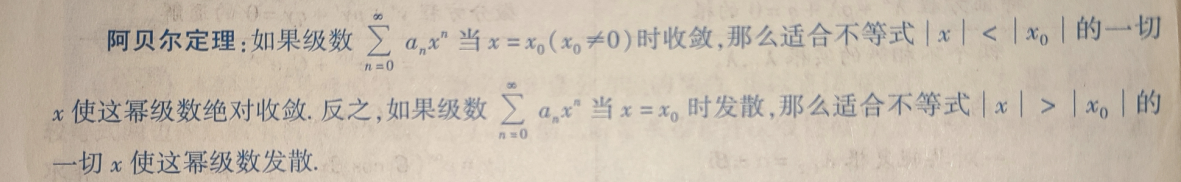



 e
x
、
s
i
n
x
、
c
o
s
x
的
收
敛
域
是
R
l
n
(
1
+
x
)
的
收
敛
域
(
−
1
,
1
】
(
1
+
x
)
a
的
收
敛
域
【
−
1
,
1
)
两
个
等
比
级
数
是
−
1
到
1
的
开
区
间
e^x、sinx、cosx的收敛域是R\\ ln(1+x)的收敛域(-1,1】\\ (1+x)^a的收敛域【-1,1)\\ 两个等比级数是-1到1的开区间
ex、sinx、cosx的收敛域是Rln(1+x)的收敛域(−1,1】(1+x)a的收敛域【−1,1)两个等比级数是−1到1的开区间
e
x
、
s
i
n
x
、
c
o
s
x
的
收
敛
域
是
R
l
n
(
1
+
x
)
的
收
敛
域
(
−
1
,
1
】
(
1
+
x
)
a
的
收
敛
域
【
−
1
,
1
)
两
个
等
比
级
数
是
−
1
到
1
的
开
区
间
e^x、sinx、cosx的收敛域是R\\ ln(1+x)的收敛域(-1,1】\\ (1+x)^a的收敛域【-1,1)\\ 两个等比级数是-1到1的开区间
ex、sinx、cosx的收敛域是Rln(1+x)的收敛域(−1,1】(1+x)a的收敛域【−1,1)两个等比级数是−1到1的开区间