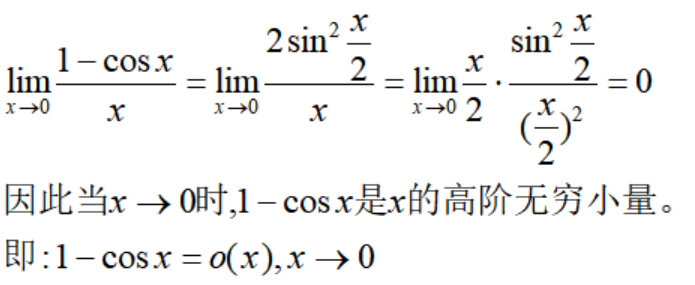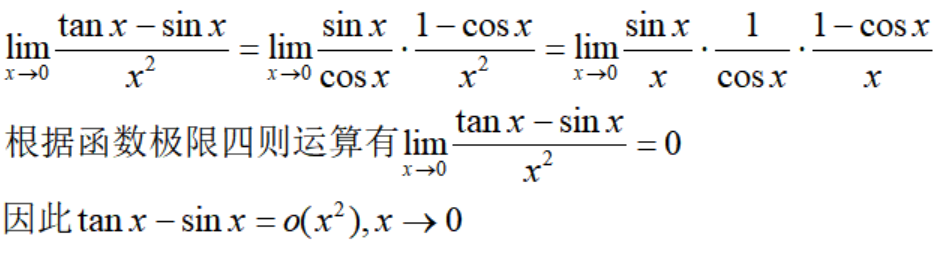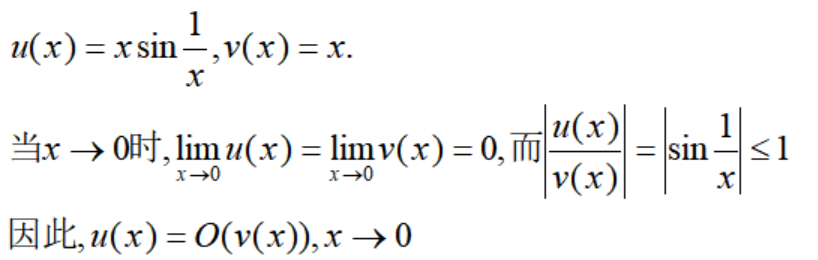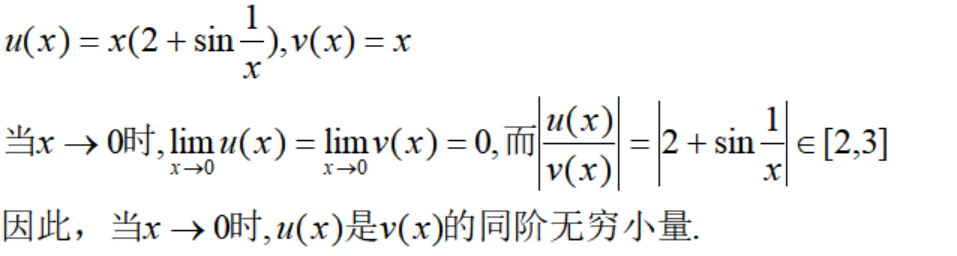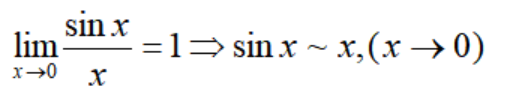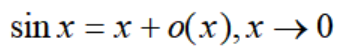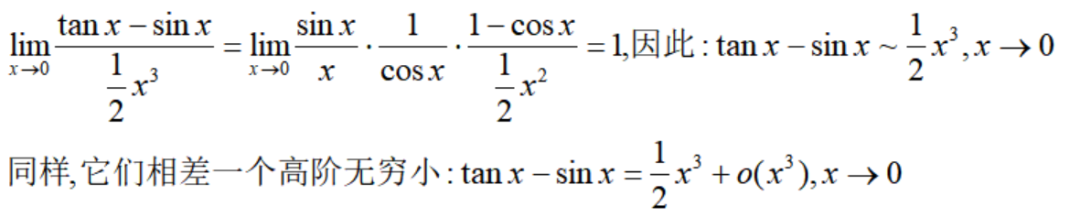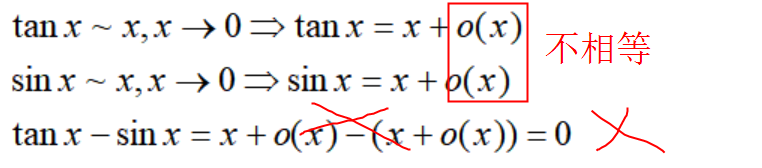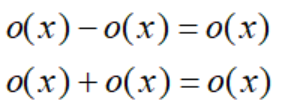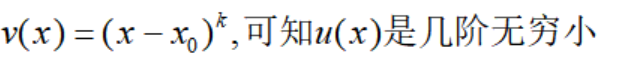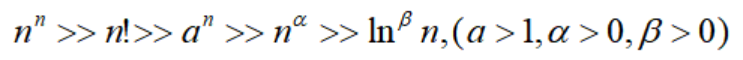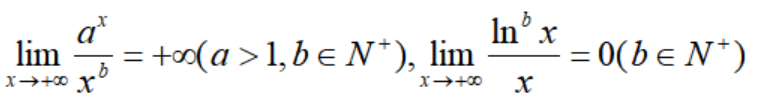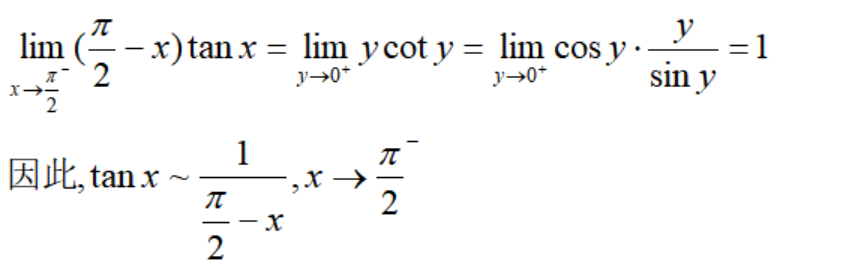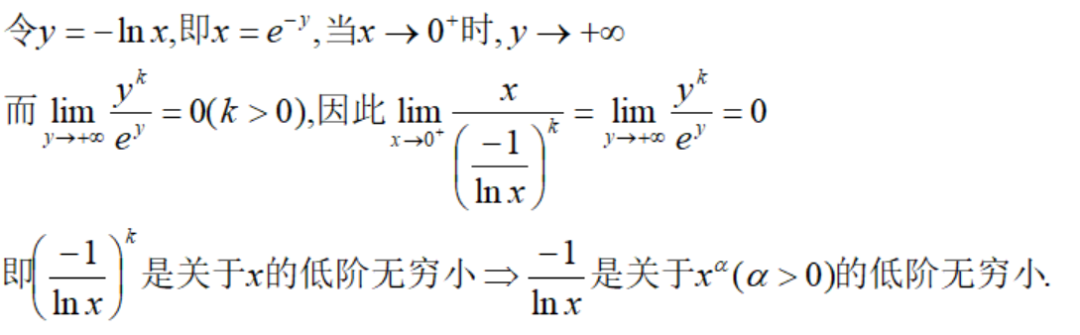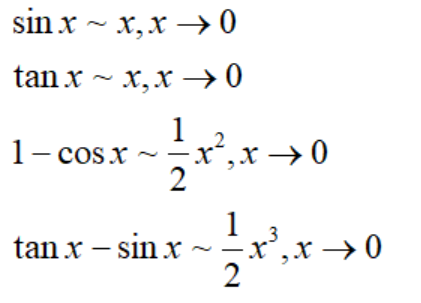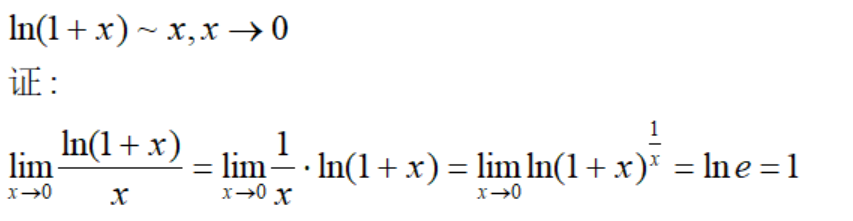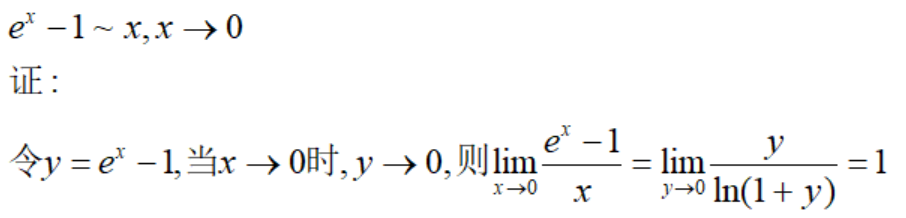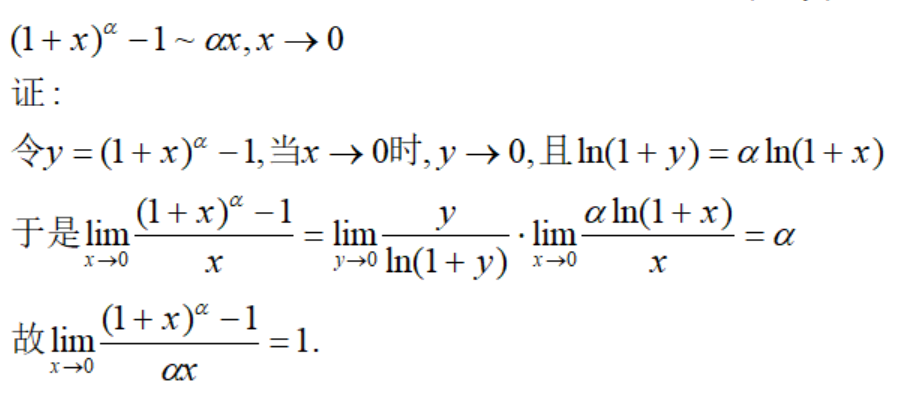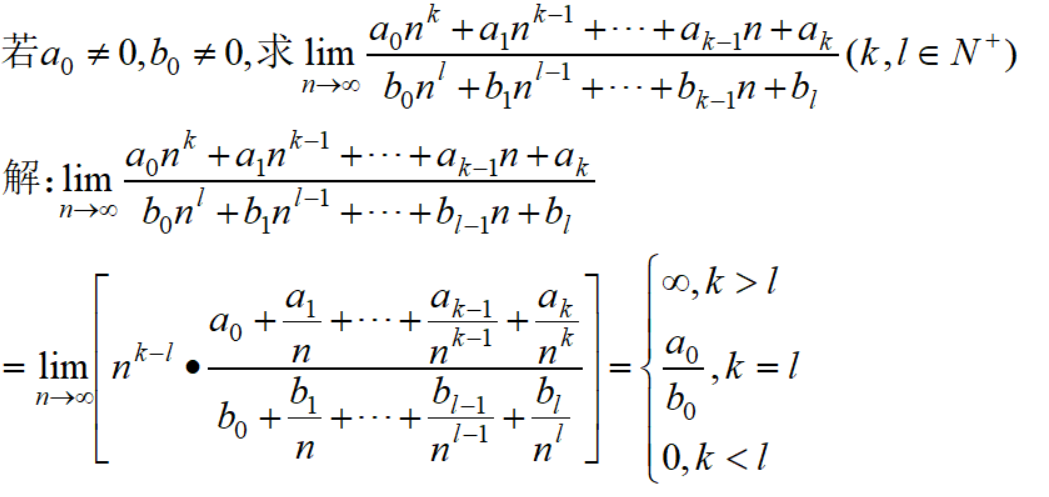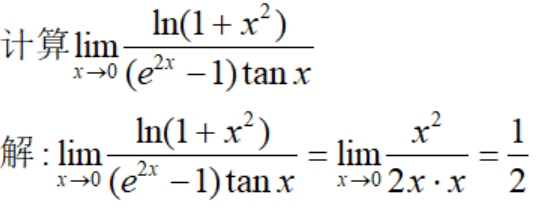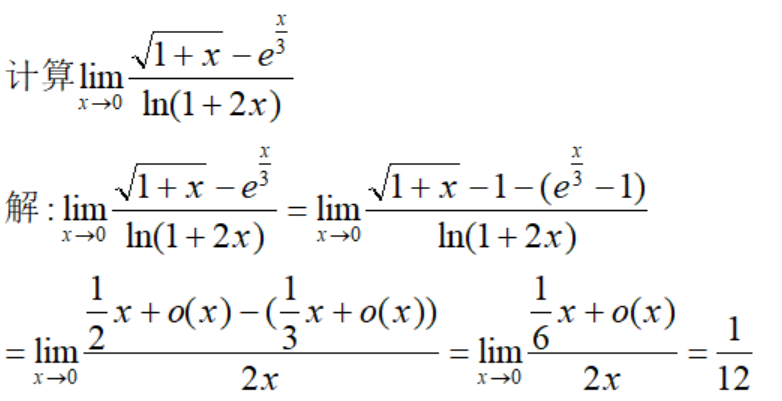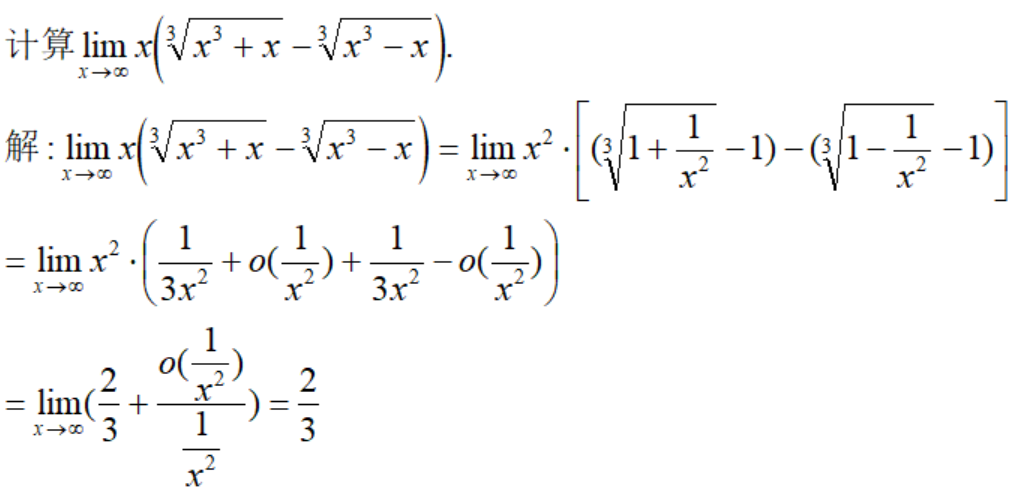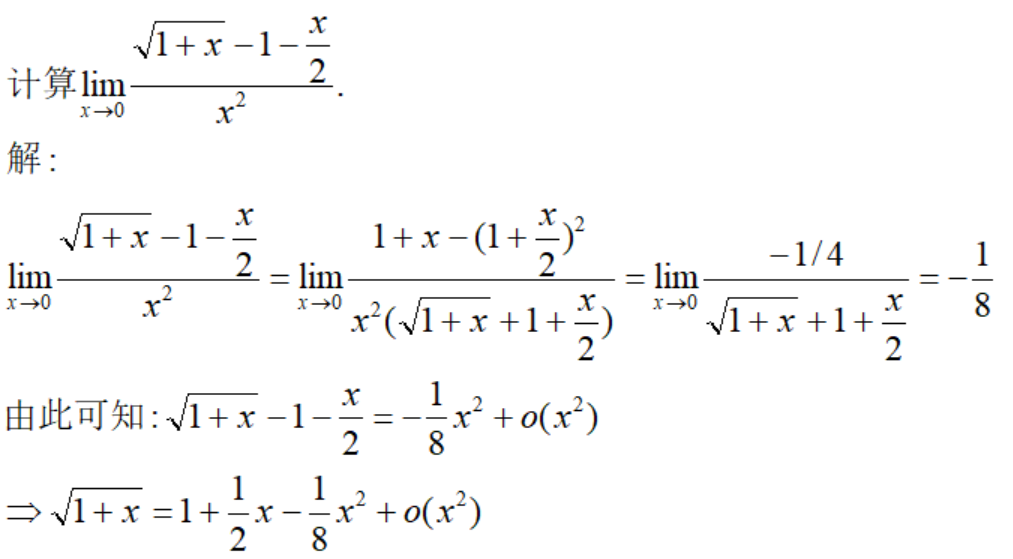1.无穷量可分为高阶无穷，同阶无穷和等价无穷

2.等价无穷小是同阶无穷小的特殊情况,等价无穷大是同阶无穷大的特殊情况

3.任何x阶数都是一个无穷小量的高阶无穷小，则这个无穷小记为o(1)

4.两个高阶无穷小量相加或相减后依然为高阶无穷小

5.在含有多个高阶无穷的式子中，其极限由最高阶无穷大量或最低阶无穷小量决定

我们提到过以0为极限的变量称为无穷小量，这个变量可以是数列也可以是函数。但需要注意两种表达：

今天，我们继续深入研究无穷小量以及与其相对的无穷大量。

1

第一种情况，是说明u(x)趋于0的速度比v(x)趋于0的速度要快得多，阶数越高，速度越快。因此称为u是v的高阶无穷小，反过来，称v是u的低阶无穷小。举两个例子：

例1

例2

对于第二种情况，表明u和v趋近于0的速度在一个量级上，趋向的速度差不多。举个例子：

例3

注意，这里的u和v不一定是同阶无穷小，因为也有可能u是v的高阶无穷小。

例4

对于第三种情况，等价无穷小其实相当于同阶无穷小的一种特殊情况，是最重要的一类无穷小，它表明u与v趋向于0的速度是一致的，比如第一类重要极限：

注意，这时候并不是说sinx与x是相等的，它们还是有差距的，它们相差一个关于x的高阶无穷小：

再举两个例子。

例5

例6

这里，要注意的是，当x趋于0时，sinx与x，tanx与x都相差一个关于x的高阶无穷小，但是它们两个是不一样的。所以下面的逻辑是错误的：

关于x的两个无穷小量进行加减运算后，依然是关于x的无穷小量：

关于无穷小量的阶，还有两点需要注意。首先，一般来说v(x)表示为：

其次，有一类特殊的无穷小——任意阶数的x都是它的高阶无穷小，记为o(1)，举个例子：

注：下面证明这个结论。

2

有无穷小量的阶，相对的也有无穷大量的阶。

在数列极限中，我们有下面不等式成立：

且它们都是无穷大量。基于此，我们可以得到很多高阶无穷大量，比如：

我们来看一个等价无穷大量的例子：

现在，我们来证明上一小节的极限。

由上面启发，可以得到下面结论：

3

对于无穷量的阶，我们最关心的是等价量。因此，有必要熟悉常用的等价量。

三角函数等价量

对数函数等价量

指数函数等价量

幂函数等价量

最后，对于一些较简单的复合函数的等价量，记住一句口诀：无穷大量看高阶，无穷小量看低阶.先看两个例子

例7

例8

这两个例子说明，在无穷小时，阶数低的项其作用，因为高阶项趋向0的速度比低阶的快得多，最终的极限由低阶项决定。相对的，讨论无穷大时，高阶项起作用，因为高阶趋于无穷的速度比低阶的快得多。在数列极限中，我们已经探讨过了：

4

我们利用等价量来求一些复杂函数的极限，先给一条定理。

例9

例10

例11

例12

最后一个等式的形式，我们以后会重点研究，它就是著名的泰勒展开公式。这里先稍微带过。