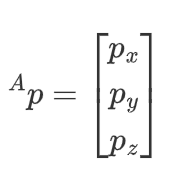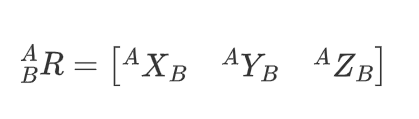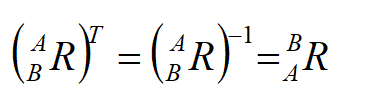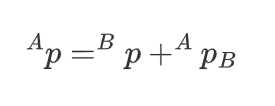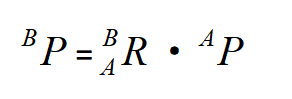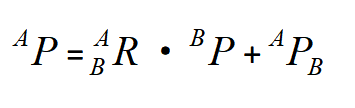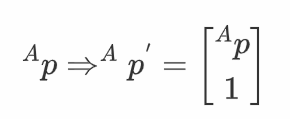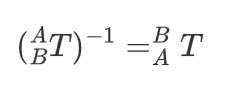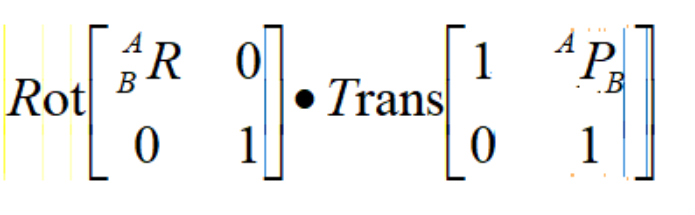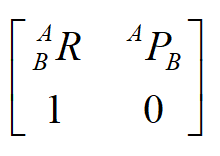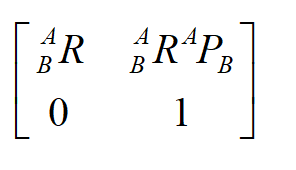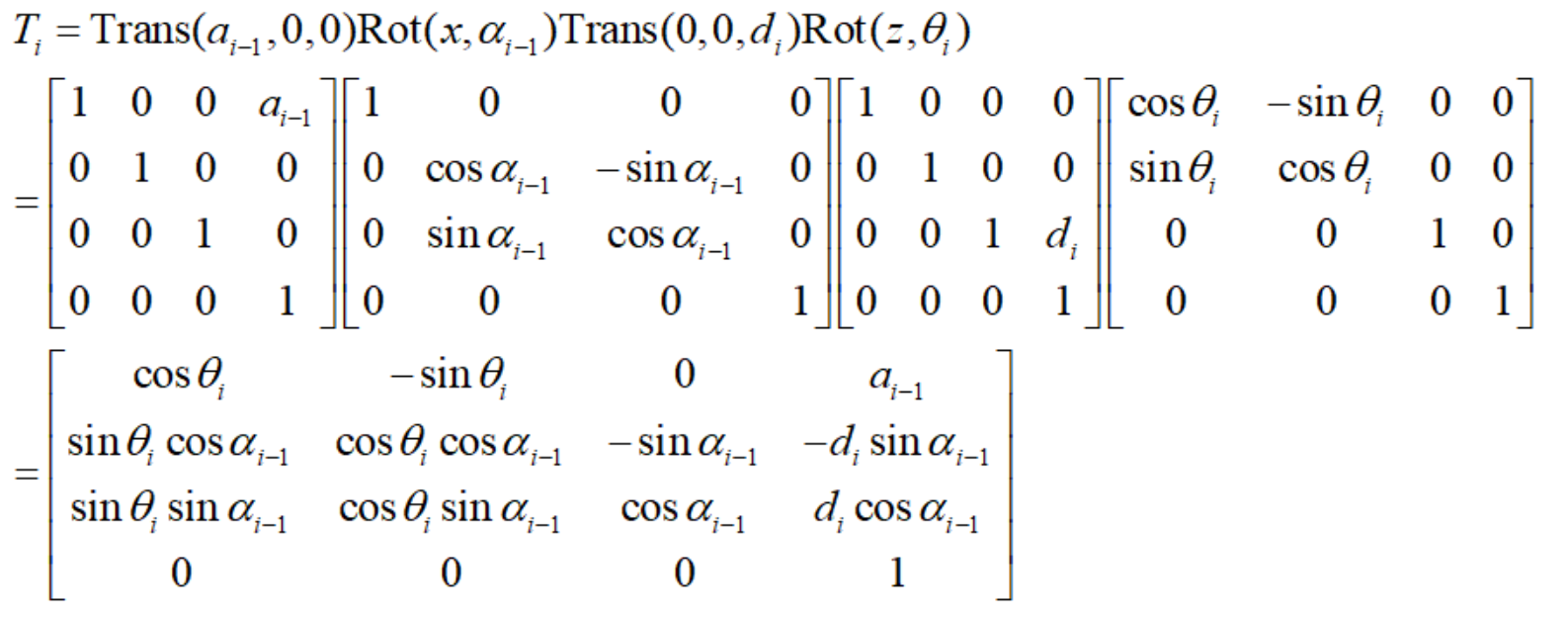【一篇文章教你搞懂 |
您所在的位置:网站首页 › 旋转基础 › 【一篇文章教你搞懂 |
【一篇文章教你搞懂
|
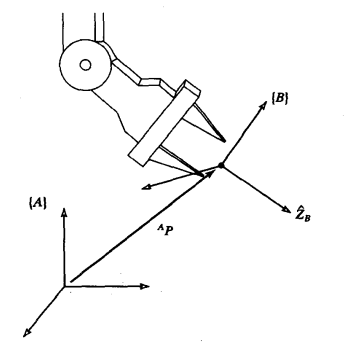
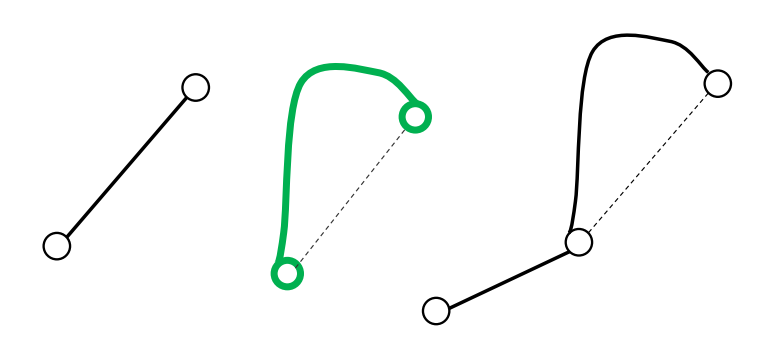
目录 一.位姿 1.简介 2.一般的矩阵表示 3.坐标变换 (1)基坐标与连体坐标 (2)变换规律 (3)绕XYZ轴的旋转变换矩阵 (4)齐次坐标变换 二.连杆变换 1.D-H参数 2.连杆变换矩阵 (1)坐标系的建立 (2)矩阵的形成 三.机器人运动学 1.正向运动学 2.逆向运动学 具体的解算与仿真案例可以看我发布的另一篇文章:【多类型运动副组合机械臂运动学解算与Matlab仿真】抬升机构+连杆机构+球窝关节机构(上) 一.位姿 1.简介位姿,即位置与姿态,为什么要引入位置与姿态,如下图所示
我们不仅经常需要表示空间的点,还经常需要描述空间中物体的姿态。例如图中矢量P直接确定了在机械臂末端的点,但只有当手的姿态已知后,机械臂的位置才能完全被确定下来,而为了描述物体的姿态,我们将在物体上固定一个坐标系并且给出此坐标系相对于参考系的表达。在图中,已知坐标系{B}被固定在物体上。{B)相对于{A}中的描述就足以表示出物体的姿态。 在机器人学中,位置和姿态经常成对出现,于是我们将此组合称作坐标系,四个矢量为一组,表示了位置和姿态信息。例如图中一个矢量表示机械臂末端的点,而另外三个量表示姿态。一个坐标系可以等价地用一个位置(矢量)矩阵和一个旋转矩阵来描述。下面教大家矩阵的基本知识以及坐标变化。 2.一般的矩阵表示 位置:
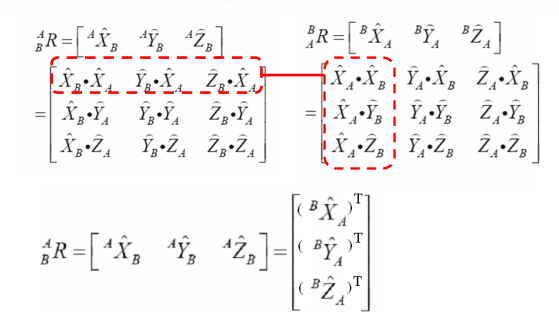
该矩阵表示为点P在A坐标系下的位置 姿态(可以简单理解为在三维空间中角度)
上述表示为在以刚体B建立空间坐标系,那么这个坐标系三个两两正交的单位矢量,在A坐标系下位置,分别记为X Y Z,也就是说,X Y Z其实是个三维列向量 某种角度来说,
从通俗角度来理解,基坐标就是指我每次进行变换的时候都用同一个坐标系;而连体坐标系是每次变换的时候用的是不同的坐标系,这些不同的坐标系之间含有某种联系 例如,一个物体在A坐标系下先平移,然后又在该坐标系下旋转,那么这就是基坐标;而另一物体在A坐标系下先绕X旋转,然后再绕旋转后坐标系的Z轴旋转,此时就是连体坐标 坐标变换是有顺序之分的,不可随意调换(矩阵乘法没有交换律),如先平移后旋转和先旋转后平移结果不同 右乘连体左乘基 若是旋转,那么就是矩阵乘法;若是平移,则是对矩阵进行加法运算 我们可以看到,在这种变换算法下矩阵的旋转和平移是分开的,并不是仅仅通过矩阵乘法来进行计算的,而齐次坐标变换解决了这个问题 (2)变换规律平移:对于平移而言,点p在A坐标系下位置等于点p在B坐标系下位置加上A,B坐标系间相对值(也就是你要平移的量),角标也相当于可约,换句话说,平移就等于原来的矩阵加上平移后的矩阵
旋转:旋转要遵守右乘连体左乘基的规则,要注意其角标是可以约掉的
齐次坐标变换是可以将平移旋转放到一个矩阵来解决问题的,由于用的是矩阵乘法,那么同样遵守右乘连体左乘基的规则 正常情况下,我们进行坐标变换是这样的:
在齐次变换中,我们将最后得到
众所周知在三位空间中,我们可以用一个三维列向量来表示一个点,所以这里是一个4 X 1矩阵;同时所有的点都可按照上面的规则变为齐次坐标 那么整个运算的过程与参与运算的矩阵如下所示:
我们称
同时,我们的齐次坐标变换矩阵还有以下性质:
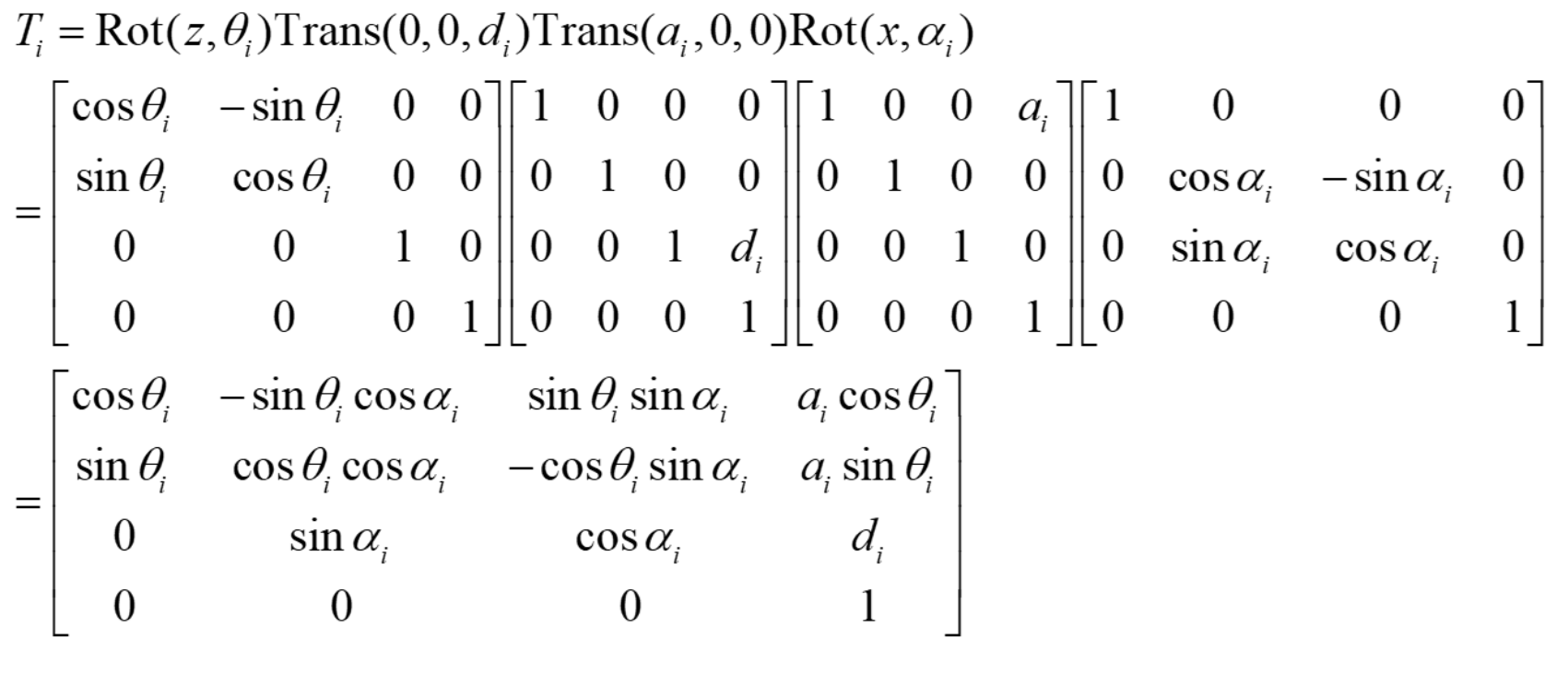
在齐次坐标下,我们将平移从原来矩阵的加法变为矩阵的乘法,旋转仍然是矩阵的乘法,实现了运算方法的统一 虽然在齐次坐标变换矩阵中既有旋转又有平移,但是遇到平移和旋转的时候,仍然需要分开进行计算,也就是分开进行矩阵乘法,他们齐次坐标变换矩阵如下:
因为矩阵乘法没有交换律存在,所以导致先旋转后平移其齐次坐标变换矩阵为
而先平移后旋转则变成
所以我们一定要分开来计算 二.连杆变换首先抛出问题:
描述两个坐标系的变换关系需要6个参数(3个表示位置变换,3个表示姿态变换),为什么DH参数只需4个? 空间任意两个坐标系的变换关系确实需要6个参数来表示,然而,在建立各个连杆的坐标系时,我们可以拟定一些规则,使得坐标系满足某些约束,从而只需4个参数则可以表示两个坐标系的变换关系。 若坐标轴
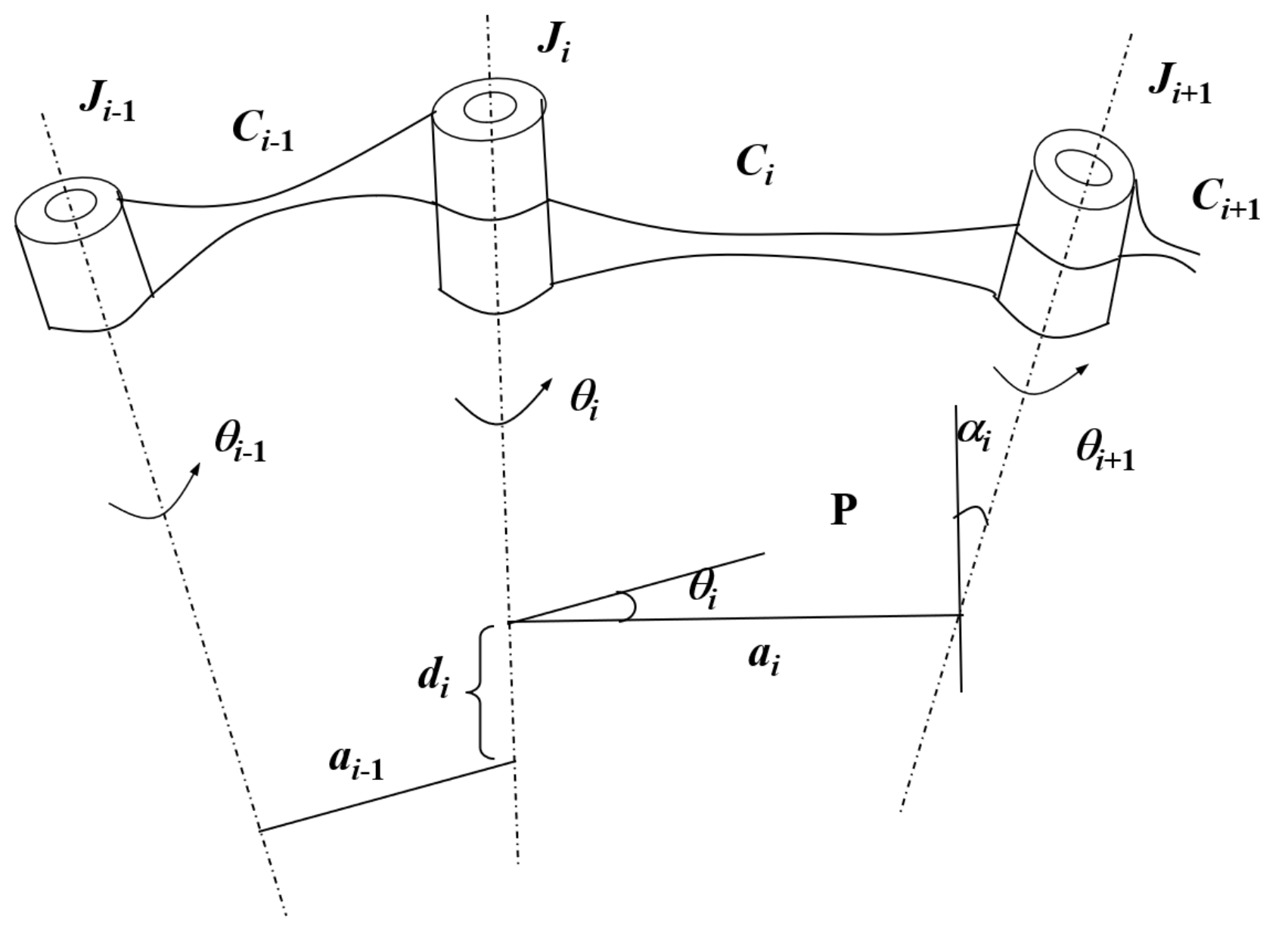
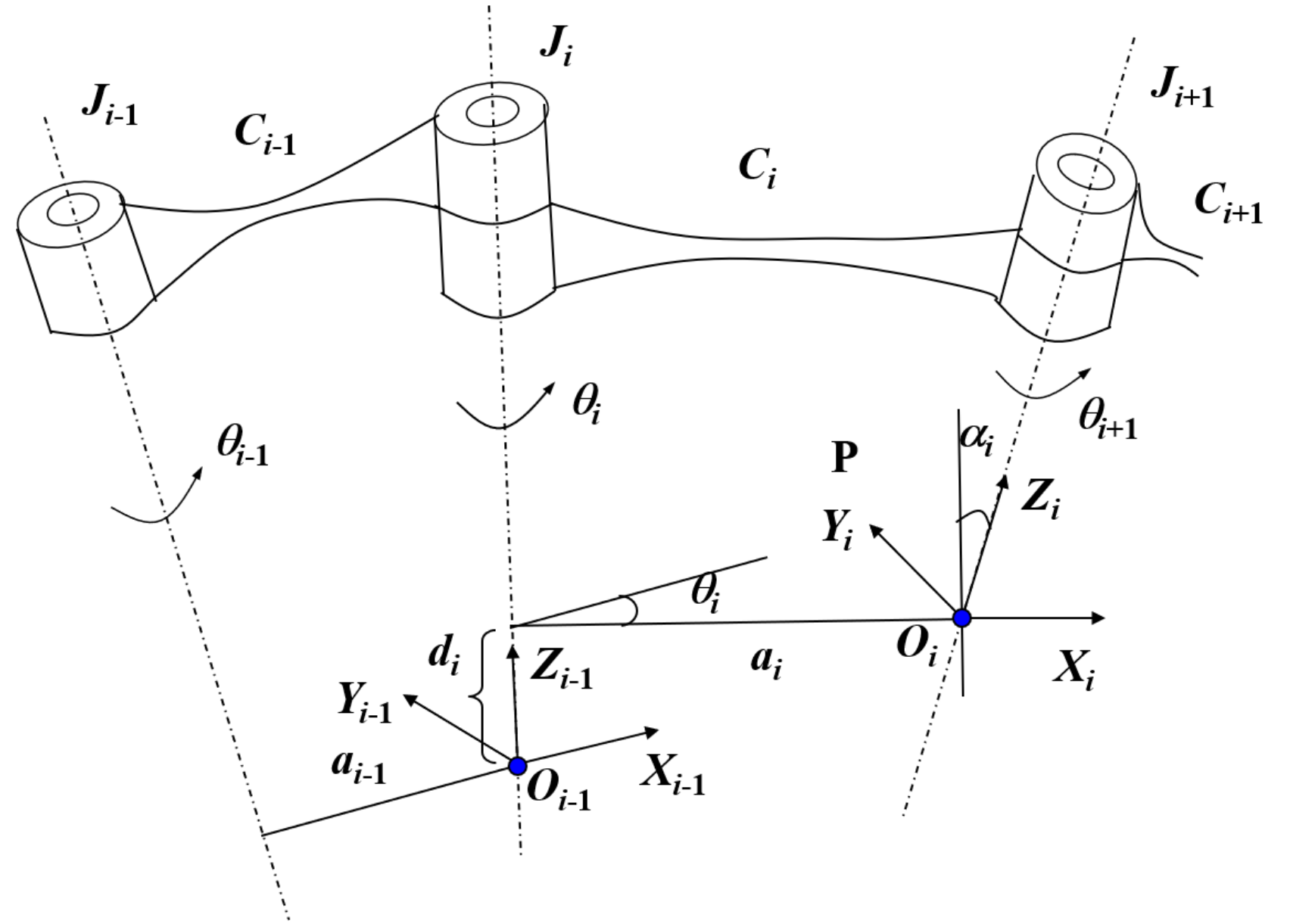
关节轴线:第i个关节的轴线记为 连杆参数: 连杆长度:两个关节的关节轴线 连杆扭转角:由 连杆偏移量:除第一和最后连杆外,中间的连杆的两个关节轴线 关节角:关节
以上图为例,我们有两个连杆,三个关节,那么坐标系的建立无非就有三种情况: 在非首尾连杆 原点
在第一连杆 原点
在最后连杆 原点
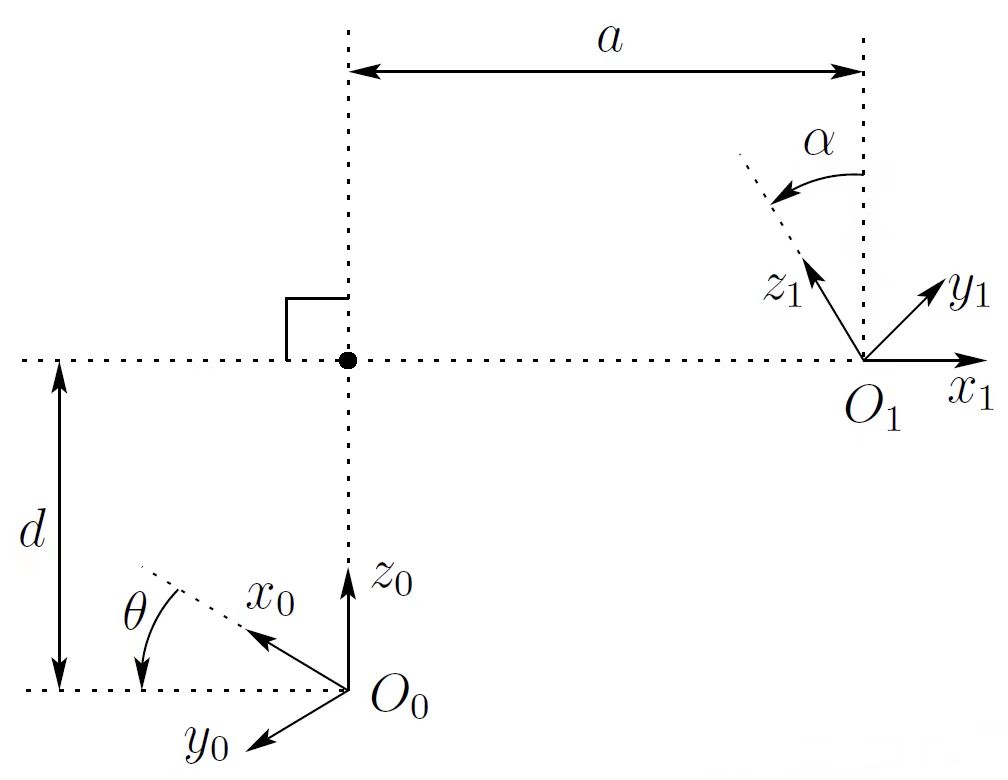
下图展示的是在
请注意,上图是在 那么我要想将 以 沿 沿新的(旋转后)的$X{i-1}$轴平移$a_i$,使新的 以 我们按照上述步骤,可以得到旋转变换矩阵,值得注意的是,每次进行变换的时候他们都不是在一个坐标系下进行的,所以是连体坐标系,他们之间是右乘的关系
机器人正向运动学解决的问题是,我知道了各种连杆的参数,然后我要求最末端的位姿 在连杆变换章节中,我们得到了连杆变换矩阵: 当
那么,我知道了连杆的参数,根据我建立坐标系的位置,可以得到连杆变换矩阵。值得注意的是,连杆变换矩阵是针对两个相邻的连杆坐标系进行变换的,也就是说各各连杆变换矩阵之间是“联体”的关系而非“基”的关系,即用右乘 那么机器人的末端姿态和位置为:
上述式子相当于是相对于第一个坐标系的位姿,不过通常我们都取第一个坐标系为基坐标系,要是相求相对于连杆
连杆变换矩阵本质上应该这么写 刚才上面提到了,我们建立的坐标系有两种,由于坐标系的建立不是唯一的,不同的坐标系下D-H矩阵是不同的,那么末端位姿不同。但对于相同的基坐标系,不同的D-H矩阵下的末端位姿相同 在机器人正向运动学中,可以看成是一个一对一关系,我有一套连杆参数,那么我一定有一个唯一的末端位姿 2.逆向运动学机器人逆向运动学解决的问题是,我知道了末端位姿,那么我连杆参数是什么呢?简单来讲,就是我知道了我末端在哪,那么我关节应该是怎样的才能让我的末端到那个位置 对于机器人逆向运动学,就不是一一对应关系了,我一个末端的位置可以对应好几套连杆参数 面对逆向运动学,其一般的解法是这样的: 已知 接下来有:
此时让矩阵间元素一一对应,即可解出一定的参数 以此类推,得出好几个上述的公式,求出其他的参数
具体的解算与仿真案例可以看我发布的另一篇文章:【多类型运动副组合机械臂运动学解算与Matlab仿真】抬升机构+连杆机构+球窝关节机构(上) |
【本文地址】