【数学和算法】梯度和方向导数 |
您所在的位置：网站首页 › 方向导数和梯度的公式 › 【数学和算法】梯度和方向导数 |
【数学和算法】梯度和方向导数
|
如果不愿意看文字描述的，这里推荐一个视频 方向导数和梯度的直观理解，里面有动态图解，很直观很形象。 -------------------------------------------------------------------- 1.什么是梯度？？百度百科对梯度的解释是：梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。 梯度方向是函数值增长最快的方向。 看了上面的定义：我就糊涂了，怎么导数还有最大值最小值之分吗？某点的导数不是一个定值?不是斜率吗？这就是我数学基础不扎实的后果。其实，我的疑问是思维局限于一元函数的导数了，需要好好补习一下多元函数的方向导数和梯度的知识。 下面是摘自百度百科对梯度的定义： 可以想象一下，大地平面为 X O Y XOY XOY所在平面( z = 0 z=0 z=0)，你现在处于山坡上的某点 P ( x , y , z ) P(x,y,z) P(x,y,z),你怎样才能最快时间跑下山坡呢? 分析一下：假设你的速度v一直都是 5 m / s 5m/s 5m/s不变，这座山假设为一个圆锥型，跑下山坡就是 Z = 0 Z=0 Z=0。很明显，你站在P点有很多方向可以跑，只有山坡朝下的方向可以跑下山坡，但是你从每个方向跑下山坡的时间各不一样，怎样才能最快到达地面呢？ 你的直觉和经验告诉你，沿着山顶点和你所站的位置的连线跑下去，就是最快的路线。这条连线的向下方向就是负梯度方向。由于梯度方向是函数值增长最快的方向，所以向下跑最快的方向的就是负梯度方向，向上跑让函数值增大的才是梯度方向。你所在点P的其中某一方向的一阶导数，就是该方向的方向导数【这个一阶导数并不是分别求x和y的偏导 ∂ f ∂ x , ∂ f ∂ y \frac{\partial{f}}{\partial{x}},\frac{\partial{f}}{\partial{y}} ∂x∂f,∂y∂f，而是 f x ∗ c o s A + f y ∗ c o s B \color{red}f_x*cosA+f_y*cosB fx∗cosA+fy∗cosB，也即 ∂ f ∂ x ∗ c o s A + ∂ f ∂ y ∗ c o s B \color{red}\frac{\partial{f}}{\partial{x}}*cosA+\frac{\partial{f}}{\partial{y}}*cosB ∂x∂f∗cosA+∂y∂f∗cosB，其中A和B分别是这个方向与X轴夹角和与Y轴夹角，并且 A + B = 90 ° A+B=90° A+B=90°】，方向导数的方向由A和B共同决定，方向导数的值是一个实数，不是向量，方向导数取得最大值的方向就是梯度方向。 上面的 A + B = 90 ° A+B=90° A+B=90°是针对二维 f ( x , y ) f(x,y) f(x,y)来说,是因为每个方向为单位向量 ( c o s A , c o s B ) (cosA , cosB) (cosA,cosB),所以 ( c o s A ) 2 + ( c o s B ) 2 = 1 \color{red}(cosA)^2 + (cosB)^2 = 1 (cosA)2+(cosB)2=1可以推出 A + B = 90 ° A+B=90° A+B=90°；对于三维 f ( x , y , z ) f(x,y,z) f(x,y,z)的话，每个方向为单位向量 ( c o s A , c o s B ， c o s C ) (cosA , cosB， cosC) (cosA,cosB，cosC)，就有 ( c o s A ) 2 + ( c o s B ) 2 + ( c o s C ) 2 = 1 \color{red}(cosA)^2 + (cosB)^2 + (cosC)^2 = 1 (cosA)2+(cosB)2+(cosC)2=1，这A、B、C的角度就不是 90 ° 90° 90°了。不要简单得把梯度方向理解为某点的斜率或一阶导数(上面360°的每个方向都有一阶导数)，因为斜率是一元一次表达式 f ( x ) = 5 x + 7 f(x)=5x+7 f(x)=5x+7在某点的斜率，或一阶导数是在一元表达式如 f ( x ) = 2 x 4 + 5 x + 7 f(x)=2x^4+5x+7 f(x)=2x4+5x+7某点的一阶导数。而梯度不限于一元，它是多个维度的变化最快的方向。 梯度是一个矢量，有大小和方向。 -------------------------------------------------------------------- 下面的公式图片源自B站视频 方向导数和梯度的直观理解。 3.方向导数定义
f
(
x
,
y
)
\color{red}f(x,y)
f(x,y)在x方向的偏导数
f
x
(
x
,
y
)
\color{red}f_x(x,y)
fx(x,y)，就是当y值不变，自变量沿着x方向变化的时候，
f
(
x
,
y
)
f(x,y)
f(x,y)的变化率。 如果x,y都变化，
f
(
x
,
y
)
f(x,y)
f(x,y)的变化率的值就是方向导数。 -------------------------------------------------------------------- 5.方向导数证明：为证明方便，以二维为例： -------------------------------------------------------------------- 6.梯度的定义
偏导数就是方向导数的一个特例，方向导数的有个特殊的方向，在这个特殊的方向下，方向导数会最大，此时方向导数就是后面要讲到的梯度，就是各个维度的偏导数组成。 -------------------------------------------------------------------- 7.举例：下面是求方向导数，不是求梯度，别搞混了。如果是求梯度，题目就不会指定
(
2
,
−
1
,
−
2
)
(2,-1,-2)
(2,−1,−2)这个方向了，因为某点的梯度方向是唯一的，不能由你指定方向。 梯度就是方向导数的模取得最大值时的向量。 |
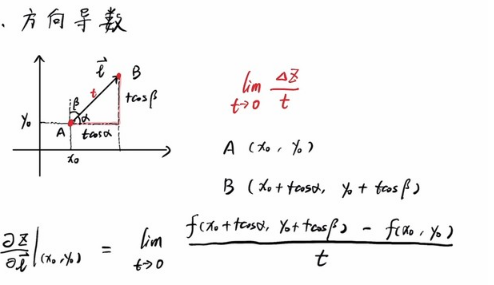
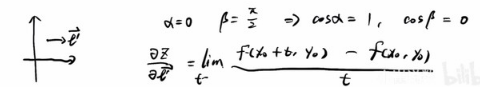
同理，三维的方向导数为： 
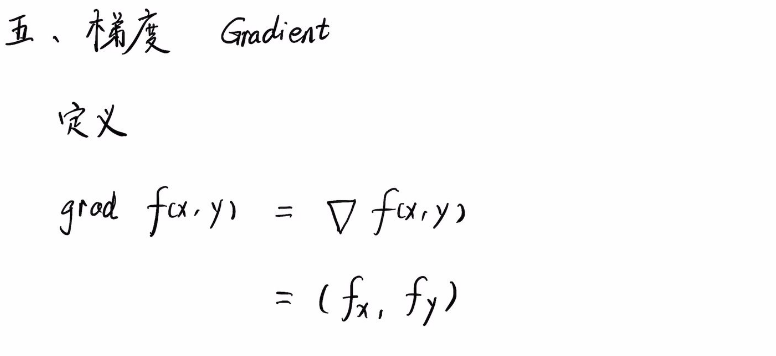
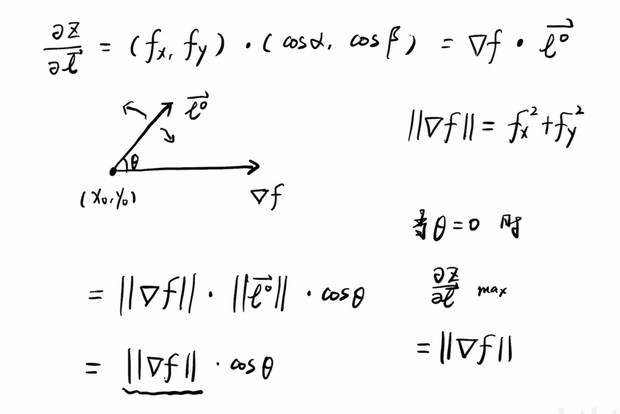当上面的
θ
=
0
\color{red}\theta=0
θ=0 时，方向导数最大，等于梯度的模。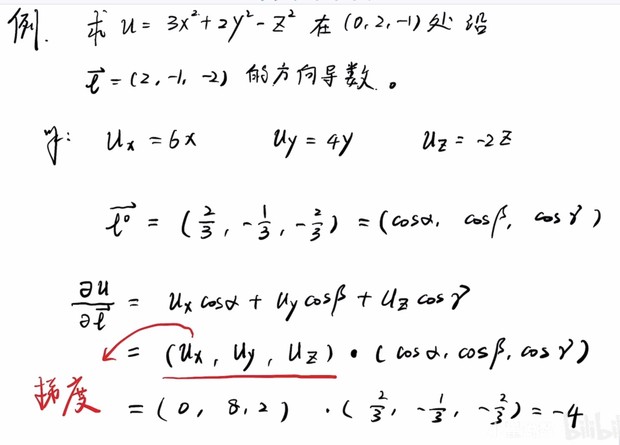
上面的三维函数
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z)的方向导数为梯度向量
(
u
x
,
u
y
,
u
z
)
\color{red}(u_x, u_y, u_z)
(ux,uy,uz) 与方向向量
(
c
o
s
A
,
c
o
s
B
，
c
o
s
C
)
(cosA , cosB， cosC)
(cosA,cosB，cosC) 做内积。其中梯度向量
(
u
x
,
u
y
,
u
z
)
(u_x, u_y, u_z)
(ux,uy,uz) 的每个元素是各个方向的偏导数。方向向量
(
c
o
s
A
,
c
o
s
B
，
c
o
s
C
)
(cosA , cosB， cosC)
(cosA,cosB，cosC) 满足
(
c
o
s
A
)
2
+
(
c
o
s
B
)
2
+
(
c
o
s
C
)
2
=
1
\color{red}(cosA)^2 + (cosB)^2 + (cosC)^2 = 1
(cosA)2+(cosB)2+(cosC)2=1。【本文地址】
今日新闻 |
推荐新闻 |