斐波那契数列的矩阵乘法方法 |
您所在的位置:网站首页 › 斐波那契数列递归算法的时间复杂度推导 › 斐波那契数列的矩阵乘法方法 |
斐波那契数列的矩阵乘法方法
|
1、求斐波那契数列矩阵乘法的方法
1.1 斐波那契数列的线性求解(
O
(
n
)
O(n)
O(n))的方法
//斐波那契数列:1 1 2 3 5 8 ...
int fibonacci(int n) {
if (n F(n−1)F(n−1)+F(n−2)arr[n]=Farr[n]=T 即在不同条件下有不同的递推式,这就没有
O
(
l
o
g
n
)
O(logn)
O(logn) 的解法。
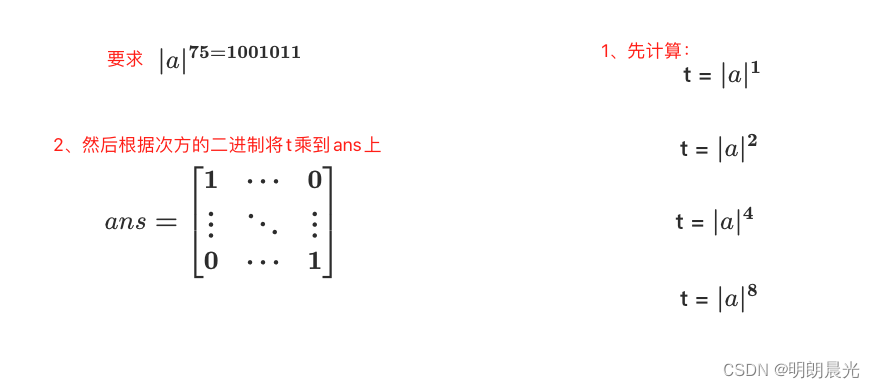
而斐波那契数列是没有条件转移的严格递推式。 怎么得到开头的行列式表示方法的? 因为 F ( n ) = F ( n − 1 ) + F ( n − 2 ) F(n) = F(n-1) + F(n-2) F(n)=F(n−1)+F(n−2),其中减得最多的是2,所有行列式的表示方法中最后要乘一个 2 阶的系数矩阵。 且一定有: ∣ F ( 3 ) F ( 2 ) ∣ = ∣ F ( 2 ) F ( 1 ) ∣ × ∣ a b c d ∣ ∣ F ( 4 ) F ( 3 ) ∣ = ∣ F ( 3 ) F ( 2 ) ∣ × ∣ a b c d ∣ \left| \begin {array}{c} F(3) & F(2) \\ \end{array}\right| = \left| \begin {array}{c} F(2) & F(1) \\ \end{array} \right| \times \left| \begin {array}{c} a & b\\ c & d \end{array} \right| \\ \\ \\ \\ \left| \begin {array}{c} F(4) & F(3) \\ \end{array}\right| = \left| \begin {array}{c} F(3) & F(2) \\ \end{array} \right| \times \left| \begin {array}{c} a & b\\ c & d \end{array} \right| \\ ∣∣F(3)F(2)∣∣=∣∣F(2)F(1)∣∣×∣∣∣∣acbd∣∣∣∣∣∣F(4)F(3)∣∣=∣∣F(3)F(2)∣∣×∣∣∣∣acbd∣∣∣∣ 现在不知道这个系数矩阵 ∣ a b c d ∣ \left|\begin{array}{c}a & b\\c & d\\\end{array}\right| ∣∣∣∣acbd∣∣∣∣ 具体的值,但是可以通过代入实际数值进行计算: 斐波那契数列:1, 1, 2, 3, 5, 8… 代入公式中,即 ∣ 2 1 ∣ = ∣ 1 1 ∣ × ∣ a b c d ∣ \left| \begin{array}{c} 2 & 1\end{array} \right| = \left| \begin{array}{c} 1 & 1\end{array} \right| \times\left|\begin{array}{c}a & b\\c & d\\\end{array}\right| ∣∣21∣∣=∣∣11∣∣×∣∣∣∣acbd∣∣∣∣ 所以 a + c = 2 b + d = 1 a + c = 2 \\ b + d = 1 a+c=2b+d=1 但仅凭这两个式子还不能算出结果,于是再多看两项: ∣ 3 2 ∣ = ∣ 2 1 ∣ × ∣ a b c d ∣ \left| \begin{array}{c} 3 & 2\end{array} \right| = \left| \begin{array}{c} 2 & 1\end{array} \right| \times\left|\begin{array}{c}a & b\\c & d\\\end{array}\right| ∣∣32∣∣=∣∣21∣∣×∣∣∣∣acbd∣∣∣∣ 所以 2 a + c = 3 2 b + d = 2 2a + c = 3\\ 2b + d = 2 2a+c=32b+d=2 求得 a = 1 , b = 1 , c = 1 , d = 0 a = 1, b = 1, c = 1, d = 0 a=1,b=1,c=1,d=0 即二阶矩阵为 ∣ 1 1 1 0 ∣ \left|\begin{array}{c}1 & 1\\1 & 0\\\end{array}\right| ∣∣∣∣1110∣∣∣∣ 通过该矩阵可以求得后续的各项。当然,也可以根据递推公式直接构造系数矩阵,见根据递推公式构造系数矩阵用于快速幂。 即: ∣ F ( 3 ) F ( 2 ) ∣ = ∣ F ( 2 ) F ( 1 ) ∣ × ∣ a b c d ∣ ∣ F ( 4 ) F ( 3 ) ∣ = ∣ F ( 3 ) F ( 2 ) ∣ × ∣ a b c d ∣ ∣ F ( 5 ) F ( 4 ) ∣ = ∣ F ( 4 ) F ( 3 ) ∣ × ∣ a b c d ∣ . . . ∣ F ( n ) F ( n − 1 ) ∣ = ∣ F ( n − 1 ) F ( n − 2 ) ∣ × ∣ a b c d ∣ \left|\begin {array}{c}F(3) & F(2) \\\end{array}\right| = \left|\begin {array}{c} F(2) & F(1) \\\end{array}\right| \times \left|\begin {array}{c}a & b\\c & d\end{array}\right| \\ \\ \\ \\ \left|\begin {array}{c}F(4) & F(3) \\\end{array}\right| = \left|\begin {array}{c} F(3) & F(2) \\\end{array}\right| \times \left|\begin {array}{c}a & b\\c & d\end{array}\right| \\ \\ \\ \left|\begin {array}{c}F(5) & F(4) \\\end{array}\right| = \left|\begin {array}{c} F(4) & F(3) \\\end{array}\right| \times \left|\begin {array}{c}a & b\\c & d\end{array}\right| \\ .\\ .\\ .\\ \\ \left|\begin {array}{c}F(n) & F(n-1) \\\end{array}\right| = \left|\begin {array}{c} F(n-1) & F(n-2) \\\end{array}\right| \times \left|\begin {array}{c}a & b\\c & d\end{array}\right| ∣∣F(3)F(2)∣∣=∣∣F(2)F(1)∣∣×∣∣∣∣acbd∣∣∣∣∣∣F(4)F(3)∣∣=∣∣F(3)F(2)∣∣×∣∣∣∣acbd∣∣∣∣∣∣F(5)F(4)∣∣=∣∣F(4)F(3)∣∣×∣∣∣∣acbd∣∣∣∣...∣∣F(n)F(n−1)∣∣=∣∣F(n−1)F(n−2)∣∣×∣∣∣∣acbd∣∣∣∣ 代入相等式后,得到: ∣ F ( n ) F ( n − 1 ) ∣ = ∣ F ( 2 ) F ( 1 ) ∣ × ∣ a b c d ∣ n − 2 \left|\begin {array}{c}F(n) & F(n-1) \\\end{array}\right| = \left|\begin {array}{c} F(2) & F(1) \\\end{array}\right| \times \left|\begin {array}{c}a & b\\c & d\end{array}\right|^{n-2} ∣∣F(n)F(n−1)∣∣=∣∣F(2)F(1)∣∣×∣∣∣∣acbd∣∣∣∣n−2 而若要求得 F ( n ) F(n) F(n) 足够快,则需要矩阵的 n n n 次方计算得足够快。 一个矩阵的 n n n 次方怎么才能计算得快? 先来解决一个基本问题:一个数的 n n n 次方怎么才能计算得快? 例如 1 0 75 10 ^ {75} 1075 怎么才能算得快呢? 流程:先得到 75 的二进制形式 1001011,然后 t = 1 0 1 t = 10^1 t=101 不断进行自乘操作,然后根据 75 的二进制位中的 1 决定是否要将 t t t 乘入结果 a n s = 1 ans = 1 ans=1 中。 64 32 16 8 4 2 1 75 = 1 0 0 1 0 1 1所以 a n s = 1 ∗ 1 0 1 ∗ 1 0 2 ∗ 1 0 8 ∗ 1 0 64 ans = 1 * 10 ^ 1 * 10^2 * 10 ^8*10^{64} ans=1∗101∗102∗108∗1064。 而在 t t t 自乘的过程中,从1次方->2次方->4次方->8次方->… n次方,一共需要 l o g n logn logn 次;再根据次方的二进制位是否为1确定是否乘入结果中,这个过程也要 l o g n logn logn 次判断,所以总体是 2 l o g n 2logn 2logn,即 O ( l o g n ) O(logn) O(logn) 可以求解出 1 0 n 10^n 10n。 这个思想的基础是二分,只不过通过二进制能分得更好。 同理,矩阵的 n n n 次方,就是: a n s = [ 1 ⋯ ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 1 ] ∗ 后 续 的 值 ans = \left[ \begin{array}{cccc} 1 & \cdots &\cdots &0\\ 0 & 1 &{\cdots} & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{array} \right] * 后续的值 ans=⎣⎢⎢⎢⎡10⋮0⋯1⋮0⋯⋯⋱⋯00⋮1⎦⎥⎥⎥⎤∗后续的值 矩阵的
n
n
n 次方计算的总体思路: 补充:矩阵乘法 1、当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。 2、矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。 3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。 矩阵的 n n n 次方的代码实现: //返回矩阵m的p次方 public static int[][] matrixPower(int[][] m, int p) { int[][] res = new int[m.length][m[0].length]; for (int i = 0; i //右移 if ((p & 1) != 0) { //p&1得到次方的二进制形式最后1位,如果为1表示当前的值需要 res = product(res, t); } t = product(t, t); } return res; } // 两个矩阵乘完之后的结果返回 public static int[][] product(int[][] a, int[][] b) { int n = a.length; //a的行数 int m = b[0].length; //b的列数 int k = a[0].length; // a的列数同时也是b的行数 int[][] ans = new int[n][m]; for(int i = 0 ; i for(int c = 0; c |
【本文地址】