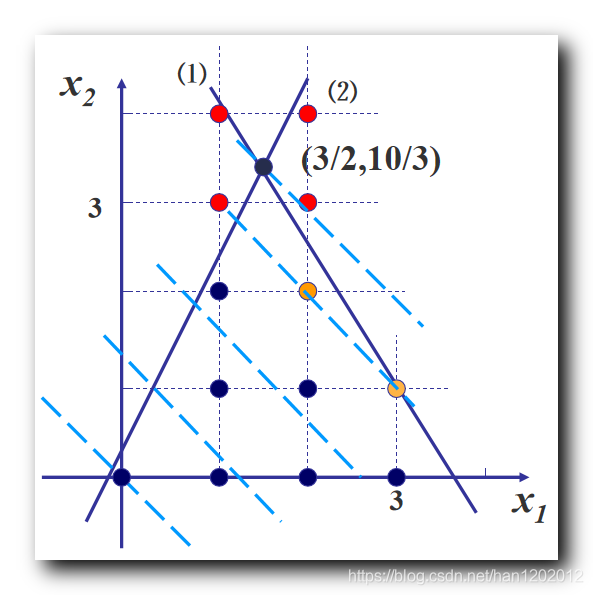
线性规划 使用 单纯形法求解 , 线性规划中的 运输规划 使用 表上作业法 求解 ;

之前讨论的都是线性规划问题 , 非线性规划如何求解 , 没有给出具体的方法 ;

整数规划问题 : 要求 一部分 或 全部 决策变量 取值整数 的规划问题 , 称为整数规划 ;

整数规划问题的松弛问题 : 不考虑 整数变量条件 , 剩余的 目标函数 和 约束条件 构成的线性规划问题 称为 整数规划问题的松弛问题 ;

整数线性规划 : 如果上述 整数规划问题的松弛问题 是线性规划 , 则称该整数规划为 整数线性规划 ;

整数规划与之前的线性规划多了一个约束条件 , 变量大于等于 0 0 0 , 并且都是整数 ;

整数线性规划数学模型一般形式 :

m a x Z = ∑ j = 0 n c j x j s . t { ∑ j = 1 n a i j x j = b i     (   i = 1 , 2 , ⋯   , m   ) x j ≥ 0     (   j = 1 , 2 , ⋯   , n   ) 部 分 或 全 部 为 整 数 \begin{array}{lcl} \rm maxZ = \sum_{j = 0}^{n} c_j x_j \\\\ \rm s.t\begin{cases} \rm \sum_{j = 1}^{n} a_{ij} x_j = b_i \ \ \ ( \ i = 1, 2, \cdots , m \ ) \\\\ \rm x_j \geq 0 \ \ \ ( \ j = 1, 2, \cdots , n \ ) 部分 或 全部 为整数 \end{cases}\end{array} maxZ=∑j=0n​cj​xj​s.t⎩⎪⎨⎪⎧​∑j=1n​aij​xj​=bi​   ( i=1,2,⋯,m )xj​≥0   ( j=1,2,⋯,n )部分或全部为整数​​

整数线性规划分为以下几类 : ① 纯整数线性规划 , ② 混合整数线性规划 , ③ 0-1 型整数线性规划 ;

① 纯整数线性规划 : 全部决策变量都 必须取值整数 的 整数线性规划 ;

② 混合整数线性规划 : 决策变量中有一部分 必须 取整数值 , 另一部分 可以不 取值整数值 的 整数线性规划 ;

③ 0-1 型整数线性规划 : 决策变量 只能取值 0 0 0 或 1 1 1 的整数线性规划 ;

资金总额 B \rm B B , 有 n n n 个投资项目 , 项目 j j j 所需的投资金额 是 a j a_j aj​ , 预期收益是 c j c_j cj​ , j = 1 , 2 , ⋯   , n j = 1,2,\cdots,n j=1,2,⋯,n ;

投资还有以下附加条件 :

① 如果投资项目 1 1 1 , 必须投资项目 2 2 2 ; 反之如果投资项目 2 2 2 , 没有限制 ;

② 项目 3 3 3 和 项目 4 4 4 必须至少选 1 1 1 个 ;

③ 项目 5 , 6 , 7 5,6,7 5,6,7 只能选择 2 2 2 个 ;

决策变量分析 : 选择合适的 决策变量 与 决策变量取值 ;

选取变量 , 使得变量的一组取值 , 能更好对应线性规划问题的解决方案 ;

每个项目有对应的两个选择 , 投资 / 不投资 , 分别使用 1 1 1 和 0 0 0 表示 ;

令 x j x_j xj​ 表示第 j j j 个项目的投资选择 , 投资 1 1 1 , 不投资 0 0 0 ; ( j = 1 , 2 , ⋯   , n j = 1,2, \cdots, n j=1,2,⋯,n )

投资额约束条件 : 所有的投资总额不能超过 B \rm B B , ∑ j = 1 n a j x j ≤ B \sum_{j = 1}^{n} a_{j} x_j \leq B ∑j=1n​aj​xj​≤B ;

分析条件 ① : 投资项目 1 1 1 , 必须投资项目 2 2 2 , 此时 x 1 = x 2 = 1 x_1 = x_2 = 1 x1​=x2​=1 ; 投资项目 2 2 2 可以投资项目 1 1 1 , 可以不投资项目 1 1 1 , 同时投资的情况上面已经分析过 , 分析后者 x 1 = 1 , x 2 = 0 , 此 时 x 1 > x 2 x_1 = 1, x_2 = 0 , 此时 x_1 > x_2 x1​=1,x2​=0,此时x1​>x2​ ; 综合上述两种情况就有 x 2 ≥ x 1 x_2 \geq x_1 x2​≥x1​ ;

分析条件 ② : 项目 3 3 3 和 项目 4 4 4 必须至少选 1 1 1 个 , 两者选择一个 , 或者都选择 , 二者相加之和是 1 1 1 或 2 2 2 ; 有约束方程 x 3 + x 4 ≥ 1 x_3 + x_4 \geq 1 x3​+x4​≥1 ;

分析条件 ③ : 项目 5 , 6 , 7 5,6,7 5,6,7 只能选择 2 2 2 个 , 则三者相加等于 2 2 2 即可 ; 约束方程 x 5 + x 6 + x 7 = 2 x_5 + x_6 + x_7 = 2 x5​+x6​+x7​=2 ;

投资问题可以表示为以下线性规划 :

m a x Z = ∑ j = 1 n c j x j s . t { ∑ j = 1 n a j x j ≤ B x 2 ≥ x 1 x 3 + x 4 ≥ 1 x 5 + x 6 + x 7 = 2 x j = 0 , 1     (   j = 1 , 2 , ⋯   , n   ) \begin{array}{lcl} \rm maxZ = \sum_{j = 1}^{n} c_j x_j \\\\ \rm s.t\begin{cases} \rm \sum_{j = 1}^{n} a_{j} x_j \leq B \\\\ \rm x_2 \geq x_1 \\\\ \rm x_3 + x_4 \geq 1 \\\\ \rm x_5 + x_6 + x_7 = 2 \\\\ \rm x_j = 0 , 1 \ \ \ ( \ j = 1, 2, \cdots , n \ ) \end{cases}\end{array} maxZ=∑j=1n​cj​xj​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​∑j=1n​aj​xj​≤Bx2​≥x1​x3​+x4​≥1x5​+x6​+x7​=2xj​=0,1   ( j=1,2,⋯,n )​​

根据 【运筹学】整数规划 ( 相关概念 | 整数规划 | 整数线性规划 | 整数线性规划分类 ) 博客中的整数线性规划概念 , 上述线性规划是 整数线性规划 ;

上述整数线性规划 的 松弛问题 是一个线性规划 , 可以使用单纯形法对其进行求解 , 求出最优解后 , 可能是小数 , 那么如何得到整数问题的最优解 , 不能进行简单的四舍五入 ;

给出 整数规划问题 ,

先求该 整数规划的松弛问题 的解 ,

松弛问题就是不考虑整数约束 , 将整数线性规划当做普通的线性规划 , 使用单纯形法求出其最优解 ;

简单的将其松弛问题最优解上下取整 , 得到的四个值 , 可能 不在可行域中 , 选择的整数解 , 必须在可行域中 ;

根据 整数规划问题的的松弛问题 的最优解 , 如何找其 整数规划问题 的整数最优解 , 是整数规划问题的核心问题 ;

整数规划问题解的特征 :

① 整数规划问题 与 松弛问题 可行解集合关系 : 整数规划问题 可行解集合 , 是该整数规划问题的 松弛问题 可行解集合 的子集 , 任意两个可行解的 凸组合 , 不一定满足整数约束条件 , 不一定是可行解 ;

② 整数规划问题 与 松弛问题 最优解关系 : 整数规划问题的可行解 一定是 其 松弛问题的可行解 , 松弛问题的可行解不一定是整数规划问题的可行解 , 整数规划问题的最优解 不会优于 松弛问题的最优解 ;

松弛问题 比 整数规划问题 条件少一些 , 整数规划问题比松弛问题变量限制多一条 " 约束变量必须都是整数 " ;

假设有如下整数规划问题 :

m a x Z = x 1 + x 2 s . t { 14 x 1 + 9 x 2 ≤ 51 − 6 x 1 + 3 x 2 ≤ 1 x 1 , x 2 ≥ 0   并 且 为 整 数 \begin{array}{lcl} \rm maxZ = x_1 + x_2 \\\\ \rm s.t\begin{cases} \rm 14 x_1 + 9x_2 \leq 51 \\\\ \rm -6 x_1 + 3x_2 \leq 1 \\\\ \rm x_1, x_2 \geq 0 \ 并且为整数 \end{cases}\end{array} maxZ=x1​+x2​s.t⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​14x1​+9x2​≤51−6x1​+3x2​≤1x1​,x2​≥0 并且为整数​​

上述整数规划问题对应的松弛问题 : 松弛问题 比 整数规划问题 条件少一些 , 整数规划问题比松弛问题变量限制多一条 " 约束变量必须都是整数 " ;

m a x Z = x 1 + x 2 s . t { 14 x 1 + 9 x 2 ≤ 51 − 6 x 1 + 3 x 2 ≤ 1 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm maxZ = x_1 + x_2 \\\\ \rm s.t\begin{cases} \rm 14 x_1 + 9x_2 \leq 51 \\\\ \rm -6 x_1 + 3x_2 \leq 1 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} maxZ=x1​+x2​s.t⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​14x1​+9x2​≤51−6x1​+3x2​≤1x1​,x2​≥0​​

使用图解法 , 解上述 松弛问题 的最优解为 { x 1 = 3 2 x 2 = 10 3 \begin{cases} \rm x_1 = \cfrac{3}{2} \\\\ \rm x_2 = \cfrac{10}{3} \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧​x1​=23​x2​=310​​

此时目标函数值 m a x Z = x 1 + x 2 = 29 6 \rm maxZ = x_1 + x_2 = \cfrac{29}{6} maxZ=x1​+x2​=629​

简单的将其松弛问题最优解上下取整 , 得到的四个点 , 如上图的四个红色点 , 都不在可行域中 , 选择的整数解 , 必须在可行域中 ;

根据 整数规划问题的的松弛问题 的最优解 , 如何找其 整数规划问题 的整数最优解 , 是整数规划问题的核心问题 ;

穷举法 ( 有局限性 ) : 直接看上图中可行域内的整数点 , 然后再逐一代入目标函数 , 得到一个 整数规划问题 的最优解 , 但是这种方法无法推广应用 , 如果点的个数比较多 , 如几万个 , 变量的维数多 , 如 10 10 10 个约束变量 , 这种方法肯定不适用 ;

整数规划问题的求解方法有 : ① 分支定界法 , ② 割平面法 ;

推荐使用 分支定界法 ;

分支定界法相关概念 :

分支 : 将一个问题不断细分为 若干子问题 , 之后逐个讨论子问题 ;

定界 : 分支很多的情况下 , 需要讨论的情况也随之增多 , 这里就需要定界 , 决定在什么时候不在进行分支 ; 满足 ① 得到最优解 , ② 根据现有条件可以排除最优解在该分支中 , 二者其一 , 就可以进行定界 ;

定界的作用是 剪掉没有讨论意义的分支 , 只讨论有意义的分支 ;

分支定界法求解整数规划步骤 :

( 1 ) 求 整数规划 的 松弛问题 最优解 :

如果 该 最优解就 是整数 , 那么得到整数规划最优解 ;

如果 该 最优解 不是整数 , 那么转到下一个步骤 分支 与 定界 ;

( 2 ) 分支 与 定界 :

任选一个 非整数解变量 x i x_i xi​ , 在 松弛问题 中加上约束 :

x i ≤ [ x i ] x_i \leq [x_i] xi​≤[xi​] 和 x i ≥ [ x i ] + 1 x_i \geq [x_i] + 1 xi​≥[xi​]+1

形成 两个新的 松弛问题 , 就是两个分支 ;

上述分支 , 分的越细致 , 限制条件越多 , 同时 最优解的质量就越差 ;

新的分支松弛问题特征 :

原问题求 最大值 时 , 目标值 是 分支问题 的上界 ;

原问题求 最小值 时 , 目标值 是 分支问题 的下界 ;

分支 1 1 1 的最优解是 x ∗ x^* x∗ , 将最优解代入目标函数后得到最优值 f 1 f_1 f1​ ;

分支 2 2 2 的最优解是 y ∗ y^* y∗ , 将最优解代入目标函数后得到最优值 f 2 f_2 f2​ ;

如果目标函数求最大值 , 那么就讨论 f 1 , f 2 f_1, f_2 f1​,f2​ 谁更大 ;

检查 分支松弛问题 的 解 及 目标函数值 :

① 得到最优整数解 : 如果该分支的 解 是 整数 , 并且 目标函数值 大于等于 其它分支的目标值 , 则剪去其它分支 , 停止计算 ;

② 没有得到最优整数解 : 如果该分支的 解 是 小数 , 并且 目标函数值 大于 整数解的目标值 , 需要 继续进行分支 , 直到得到最优解 ;

假设考虑 分支 1 1 1 松弛问题 , 每次都要给问题找到一个界 , 开始先使用观察法找到一个界 , 找到一个整数解 f f f , 将该解代入目标函数 , 然后在 不断地计算中, 修改该界 ;

假设 分支 1 1 1 松弛问题 目标函数 求最大值 ,

如果求解 分支 1 1 1 松弛问题 最优解 恰好也是一个整数解 f 0 f_0 f0​ , 如果 f 0 > f f_0 > f f0​>f , 此时需要重新定界 , 将 f 0 f_0 f0​ 作为新的界来讨论 ;

根据新的界来看 分支 2 2 2 松弛问题是否需要讨论 , 求出 分支 2 2 2 的最优解 对应的 目标函数最优值 f ∗ f^* f∗ ;

如果 分支 2 2 2 的最优值 小于 分支 1 1 1 的最优值 f ∗ ≤ f 0 f^* \leq f^0 f∗≤f0 , 此时分支 2 2 2 不用再进行分支了 , 再进行分支 , 其最优值会越来越差 ;

定界法的作用是将不符合条件的分支剪去 ;

如上篇博客 【运筹学】整数规划 ( 整数规划问题解的特征 | 整数规划问题 与 松弛问题 示例 ) 中 , 求解如下 整数规划 解 :

m a x Z = x 1 + x 2 s . t { 14 x 1 + 9 x 2 ≤ 51 − 6 x 1 + 3 x 2 ≤ 1 x 1 , x 2 ≥ 0   并 且 为 整 数 \begin{array}{lcl} \rm maxZ = x_1 + x_2 \\\\ \rm s.t\begin{cases} \rm 14 x_1 + 9x_2 \leq 51 \\\\ \rm -6 x_1 + 3x_2 \leq 1 \\\\ \rm x_1, x_2 \geq 0 \ 并且为整数 \end{cases}\end{array} maxZ=x1​+x2​s.t⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​14x1​+9x2​≤51−6x1​+3x2​≤1x1​,x2​≥0 并且为整数​​

其对应的松弛问题是 : 去掉整数解限制 ;

m a x Z = x 1 + x 2 s . t { 14 x 1 + 9 x 2 ≤ 51 − 6 x 1 + 3 x 2 ≤ 1 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm maxZ = x_1 + x_2 \\\\ \rm s.t\begin{cases} \rm 14 x_1 + 9x_2 \leq 51 \\\\ \rm -6 x_1 + 3x_2 \leq 1 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} maxZ=x1​+x2​s.t⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​14x1​+9x2​≤51−6x1​+3x2​≤1x1​,x2​≥0​​

分支都是基于松弛问题进行的 , 为松弛问题分支 , 组成两个新的松弛问题 ;

下图是求解结果 ( 图解法 ) :

最优解 x 1 = 3 2 x_1 = \cfrac{3}{2} x1​=23​ , 分别为 x 1 x_1 x1​ 添加 x i ≤ [ x i ] x_i \leq [x_i] xi​≤[xi​] 和 x i ≥ [ x i ] + 1 x_i \geq [x_i] + 1 xi​≥[xi​]+1 约束 , 形成两个新的线性规划 ;

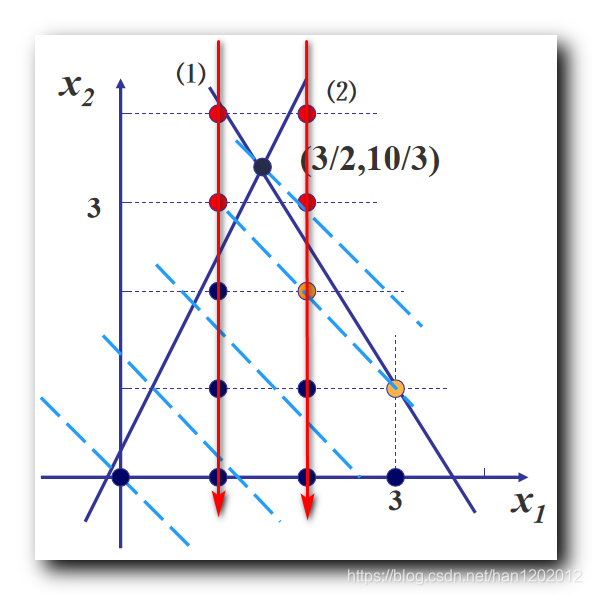
分支 1 1 1 整数规划 : 添加 x i ≤ [ x i ] x_i \leq [x_i] xi​≤[xi​] 约束 , 即 x 1 ≤ 1 x_1 \leq 1 x1​≤1 ;

m a x Z = x 1 + x 2 s . t { 14 x 1 + 9 x 2 ≤ 51 − 6 x 1 + 3 x 2 ≤ 1 x 1 ≤ 1 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm maxZ = x_1 + x_2 \\\\ \rm s.t\begin{cases} \rm 14 x_1 + 9x_2 \leq 51 \\\\ \rm -6 x_1 + 3x_2 \leq 1 \\\\ \rm x_1 \leq 1 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} maxZ=x1​+x2​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​14x1​+9x2​≤51−6x1​+3x2​≤1x1​≤1x1​,x2​≥0​​

分支 2 2 2 整数规划 : 添加 x i ≥ [ x i ] + 1 x_i \geq [x_i] +1 xi​≥[xi​]+1 约束 , 即 x 1 ≥ 2 x_1 \geq 2 x1​≥2 ;

m a x Z = x 1 + x 2 s . t { 14 x 1 + 9 x 2 ≤ 51 − 6 x 1 + 3 x 2 ≤ 1 x 1 ≥ 2 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm maxZ = x_1 + x_2 \\\\ \rm s.t\begin{cases} \rm 14 x_1 + 9x_2 \leq 51 \\\\ \rm -6 x_1 + 3x_2 \leq 1 \\\\ \rm x_1 \geq 2 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} maxZ=x1​+x2​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​14x1​+9x2​≤51−6x1​+3x2​≤1x1​≥2x1​,x2​≥0​​

这样就将一个线性规划 , 分解成了两个问题分支 , 分别找两个分支问题的所有整数解 ;

整数规划的整数解 , 肯定在上述两个分支之一中 , 中间将一部分可行域排除在外了 , 就是下图中两个红色箭头之间的可行域部分 , 被排除掉的部分肯定没有整数解 , 都是小数 ;

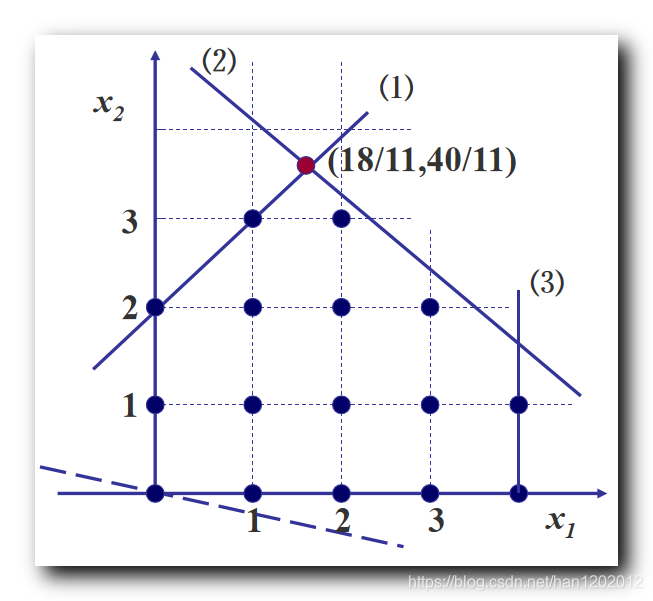
使用 分支定界法 求如下整数规划 :

m i n W = − x 1 − 5 x 2 s . t { x 1 − x 2 ≥ − 2 5 x 1 + 6 x 2 ≤ 30 x 1 ≤ 4 x 1 , x 2 ≥ 0   并 且 为 整 数 \begin{array}{lcl} \rm min W = -x_1 -5 x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - x_2 \geq -2 \\\\ \rm 5x_1 + 6x_2 \leq 30 \\\\ \rm x_1 \leq 4 \\\\ \rm x_1, x_2 \geq 0 \ 并且为整数 \end{cases}\end{array} minW=−x1​−5x2​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​x1​−x2​≥−25x1​+6x2​≤30x1​≤4x1​,x2​≥0 并且为整数​​

求上述整数规划 ( I P \rm IP IP ) 的松弛问题 ( L P \rm LP LP ) : 去掉整数限制即可得到一个一般的线性规划 ;

m i n W = − x 1 − 5 x 2 s . t { x 1 − x 2 ≥ − 2 5 x 1 + 6 x 2 ≤ 30 x 1 ≤ 4 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm min W = -x_1 -5 x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - x_2 \geq -2 \\\\ \rm 5x_1 + 6x_2 \leq 30 \\\\ \rm x_1 \leq 4 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} minW=−x1​−5x2​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​x1​−x2​≥−25x1​+6x2​≤30x1​≤4x1​,x2​≥0​​

可以使用单纯形法求上述线性规划的最优解 , 本次使用图示法 , 求的最优化 ;

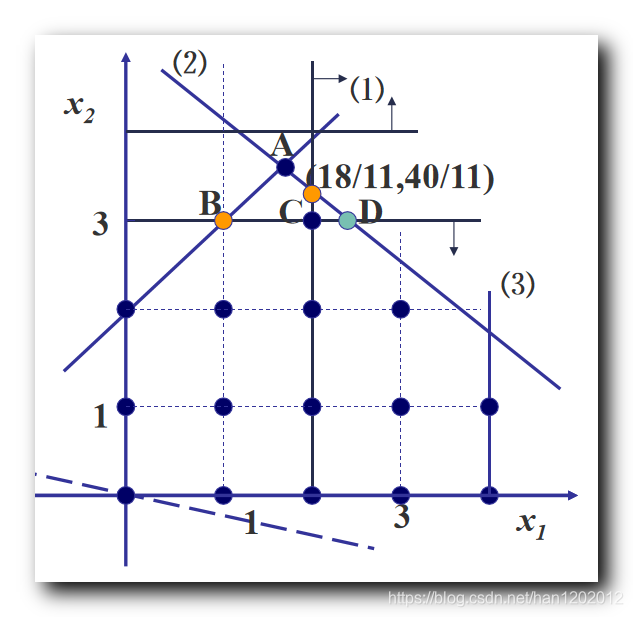
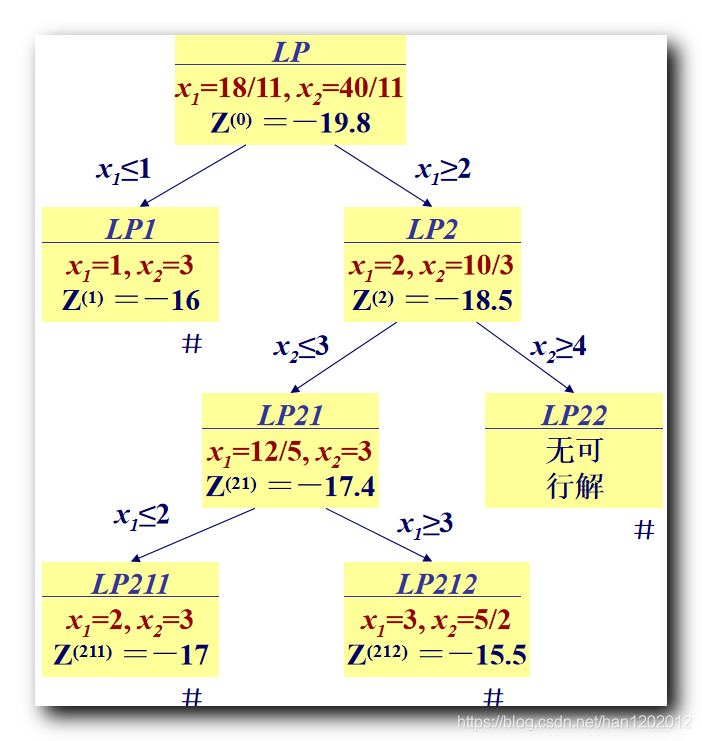
使用图示法解得上述 松弛问题 最优解 { x 1 = 18 11 ≈ 1.64 x 2 = 40 11 ≈ 3.64 \begin{cases} \rm x_1 = \cfrac{18}{11} \approx 1.64 \\\\ \rm x_2 = \cfrac{40}{11} \approx 3.64 \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧​x1​=1118​≈1.64x2​=1140​≈3.64​ , 将上述最优解代入约束方程 ,

得到整数规划最小值 m i n W = − x 1 − 5 x 2 = − 218 11 ≈ − 19.8 \rm min W = -x_1 -5 x_2 = - \cfrac{218}{11} \approx -19.8 minW=−x1​−5x2​=−11218​≈−19.8

如果上述 松弛问题 最优解 是整数 , 则该整数线性规划的最优解就是 松弛问题 的最优解 ;

上述 松弛问题 L P \rm LP LP 最优解不是整数 , 这里需要进行 分支 操作 , 分成两个 分支松弛问题 L P 1 \rm LP1 LP1 和 L P 2 \rm LP2 LP2 ;

分支操作 : 任选一个 非整数解变量 x i x_i xi​ , 在 松弛问题 中加上约束 , x i ≤ [ x i ] x_i \leq [x_i] xi​≤[xi​] 和 x i ≥ [ x i ] + 1 x_i \geq [x_i] + 1 xi​≥[xi​]+1 , 形成 两个新的 松弛问题 , 就是两个分支 ;

选择 非整数取值的变量 x 1 = 18 11 ≈ 1.64 x_1 = \cfrac{18}{11} \approx 1.64 x1​=1118​≈1.64 , 作为分支变量 ,

x i ≤ [ x i ] x_i \leq [x_i] xi​≤[xi​] 对应的 分支新增约束条件是 x 1 ≤ 1 x_1 \leq 1 x1​≤1 ;

x i ≥ [ x i ] + 1 x_i \geq [x_i] + 1 xi​≥[xi​]+1 对应的 分支新增约束条件是 x 1 ≥ 2 x_1 \geq 2 x1​≥2 ;

在 L P 1 \rm LP1 LP1 分支松弛问题中加入 x 1 ≤ 1 x_1 \leq 1 x1​≤1 条件后为 :

m i n W = − x 1 − 5 x 2 s . t { x 1 − x 2 ≥ − 2 5 x 1 + 6 x 2 ≤ 30 x 1 ≤ 4 x 1 ≤ 1 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm min W = -x_1 -5 x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - x_2 \geq -2 \\\\ \rm 5x_1 + 6x_2 \leq 30 \\\\ \rm x_1 \leq 4 \\\\ \rm x_1 \leq 1 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} minW=−x1​−5x2​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​x1​−x2​≥−25x1​+6x2​≤30x1​≤4x1​≤1x1​,x2​≥0​​

求上述 L P 1 \rm LP1 LP1 分支的最优解 { x 1 = 1 x 2 = 3 \begin{cases} \rm x_1 = 1 \\\\ \rm x_2 = 3 \end{cases} ⎩⎪⎨⎪⎧​x1​=1x2​=3​ , 将上述最优解代入约束方程 ,

得到整数规划最小值 m i n W = − x 1 − 5 x 2 = − 16 \rm min W = -x_1 -5 x_2 = - 16 minW=−x1​−5x2​=−16

L P 1 \rm LP1 LP1 分支的界就是 − 16 -16 −16 ;

在 L P 2 \rm LP2 LP2 分支松弛问题中加入 x 1 ≥ 2 x_1 \geq 2 x1​≥2 条件后为 :

m i n W = − x 1 − 5 x 2 s . t { x 1 − x 2 ≥ − 2 5 x 1 + 6 x 2 ≤ 30 x 1 ≤ 4 x 1 ≥ 2 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm min W = -x_1 -5 x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - x_2 \geq -2 \\\\ \rm 5x_1 + 6x_2 \leq 30 \\\\ \rm x_1 \leq 4 \\\\ \rm x_1 \geq 2 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} minW=−x1​−5x2​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​x1​−x2​≥−25x1​+6x2​≤30x1​≤4x1​≥2x1​,x2​≥0​​

求上述 L P 2 \rm LP2 LP2 分支的最优解 { x 1 = 2 x 2 = 10 3 \begin{cases} \rm x_1 = 2 \\\\ \rm x_2 = \cfrac{10}{3} \end{cases} ⎩⎪⎪⎨⎪⎪⎧​x1​=2x2​=310​​ , 将上述最优解代入约束方程 ,

得到整数规划最小值 m i n W = − x 1 − 5 x 2 = − 56 3 ≈ − 18.7 \rm min W = -x_1 -5 x_2 = - \cfrac{56}{3} \approx -18.7 minW=−x1​−5x2​=−356​≈−18.7

L P 2 \rm LP2 LP2 分支的目标值是 − 18.7 -18.7 −18.7 ;

L P 1 \rm LP1 LP1 分支的最优解时整数 , 界 是 − 16 -16 −16 ,

L P 2 \rm LP2 LP2 分支目标值还不是整数 , 因此需要继续分支 ;

判定某个分支 松弛问题 是否继续向下分支的依据 :

① 根据整最优解是否是整数判定 : 首先看 分支 松弛问题 最优解 是否是整数 , 如果是那就停下来 , 如果不是继续向下分支 ;

② 根据界的优劣判定 ( 定界思想 ) : 是否继续向下分支 , 还需要看 界 的值 , 通过该 界 的值 , 讨论是否继续向下分支 ;

L P 2 \rm LP2 LP2 继续向下分支 , x 1 x_1 x1​ 变量已经是整数变量了 ,

这里 选择 非整数取值的变量 x 2 = 10 3 ≈ 3.33 x_2 = \cfrac{10}{3} \approx 3.33 x2​=310​≈3.33 , 作为分支变量 ,

x i ≤ [ x i ] x_i \leq [x_i] xi​≤[xi​] 对应的 分支新增约束条件是 x 2 ≤ 3 x_2 \leq 3 x2​≤3 ;

x i ≥ [ x i ] + 1 x_i \geq [x_i] + 1 xi​≥[xi​]+1 对应的 分支新增约束条件是 x 2 ≥ 4 x_2 \geq 4 x2​≥4 ;

这里得到了 L P 2 \rm LP2 LP2 分支下的两个 分支松弛问题 L P 21 \rm LP21 LP21 和 L P 22 \rm LP22 LP22 ;

在 L P 21 \rm LP21 LP21 分支松弛问题中加入 x 2 ≤ 3 x_2 \leq 3 x2​≤3 条件后为 :

m i n W = − x 1 − 5 x 2 s . t { x 1 − x 2 ≥ − 2 5 x 1 + 6 x 2 ≤ 30 x 1 ≤ 4 x 1 ≥ 2 x 2 ≤ 3 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm min W = -x_1 -5 x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - x_2 \geq -2 \\\\ \rm 5x_1 + 6x_2 \leq 30 \\\\ \rm x_1 \leq 4 \\\\ \rm x_1 \geq 2 \\\\ \rm x_2 \leq 3 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} minW=−x1​−5x2​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​x1​−x2​≥−25x1​+6x2​≤30x1​≤4x1​≥2x2​≤3x1​,x2​≥0​​

求上述 L P 21 \rm LP21 LP21 分支的最优解 { x 1 = 12 5 = 2.4 x 2 = 3 \begin{cases} \rm x_1 = \cfrac{12}{5} = 2.4 \\\\ \rm x_2 = 3 \end{cases} ⎩⎪⎪⎨⎪⎪⎧​x1​=512​=2.4x2​=3​ , 将上述最优解代入约束方程 ,

得到整数规划最小值 m i n W = − x 1 − 5 x 2 = − 17.4 \rm min W = -x_1 -5 x_2 = - 17.4 minW=−x1​−5x2​=−17.4

L P 21 \rm LP21 LP21 分支的最优解不是整数 , 而且比 L P 1 \rm LP1 LP1 分支的界 − 16 -16 −16 要好 , 可需要继续分支 ;

在 L P 22 \rm LP22 LP22 分支松弛问题中加入 x 2 ≥ 4 x_2 \geq 4 x2​≥4 条件后为 :

m i n W = − x 1 − 5 x 2 s . t { x 1 − x 2 ≥ − 2 5 x 1 + 6 x 2 ≤ 30 x 1 ≤ 4 x 1 ≥ 2 x 2 ≥ 4 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm min W = -x_1 -5 x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - x_2 \geq -2 \\\\ \rm 5x_1 + 6x_2 \leq 30 \\\\ \rm x_1 \leq 4 \\\\ \rm x_1 \geq 2 \\\\ \rm x_2 \geq 4 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} minW=−x1​−5x2​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​x1​−x2​≥−25x1​+6x2​≤30x1​≤4x1​≥2x2​≥4x1​,x2​≥0​​

上述 L P 22 \rm LP22 LP22 分支 没有可行解 , 直接停止 ;

L P 21 \rm LP21 LP21 继续向下分支 ,

这里 选择 非整数取值的变量 x 1 = 12 5 = 2.4 x_1 = \cfrac{12}{5} = 2.4 x1​=512​=2.4 , 作为分支变量 ,

x i ≤ [ x i ] x_i \leq [x_i] xi​≤[xi​] 对应的 分支新增约束条件是 x 1 ≤ 2 x_1 \leq 2 x1​≤2 ;

x i ≥ [ x i ] + 1 x_i \geq [x_i] + 1 xi​≥[xi​]+1 对应的 分支新增约束条件是 x 1 ≥ 3 x_1 \geq 3 x1​≥3 ;

这里得到了 L P 21 \rm LP21 LP21 分支下的两个 分支松弛问题 L P 211 \rm LP211 LP211 和 L P 212 \rm LP212 LP212 ;

在 L P 211 \rm LP211 LP211 分支松弛问题中加入 x 1 ≤ 2 x_1 \leq 2 x1​≤2 条件后为 :

m i n W = − x 1 − 5 x 2 s . t { x 1 − x 2 ≥ − 2 5 x 1 + 6 x 2 ≤ 30 x 1 ≤ 4 x 1 ≥ 2 x 1 ≤ 2 x 2 ≤ 3 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm min W = -x_1 -5 x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - x_2 \geq -2 \\\\ \rm 5x_1 + 6x_2 \leq 30 \\\\ \rm x_1 \leq 4 \\\\ \rm x_1 \geq 2 \\\\ \rm x_1 \leq 2 \\\\ \rm x_2 \leq 3 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} minW=−x1​−5x2​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​x1​−x2​≥−25x1​+6x2​≤30x1​≤4x1​≥2x1​≤2x2​≤3x1​,x2​≥0​​

求上述 L P 211 \rm LP211 LP211 分支的最优解 { x 1 = 2 x 2 = 3 \begin{cases} \rm x_1 = 2 \\\\ \rm x_2 = 3 \end{cases} ⎩⎪⎨⎪⎧​x1​=2x2​=3​ , 将上述最优解代入约束方程 ,

得到整数规划最小值 m i n W = − x 1 − 5 x 2 = − 17 \rm min W = -x_1 -5 x_2 = - 17 minW=−x1​−5x2​=−17

L P 21 \rm LP21 LP21 分支的最优解是整数 , 而且比 L P 1 \rm LP1 LP1 分支的界 − 16 -16 −16 要好 , 是当前最好的 界 ;

因此这里将 界 更新为 − 17 -17 −17 ;

在 L P 212 \rm LP212 LP212 分支松弛问题中加入 x 1 ≥ 3 x_1 \geq 3 x1​≥3 条件后为 :

m i n W = − x 1 − 5 x 2 s . t { x 1 − x 2 ≥ − 2 5 x 1 + 6 x 2 ≤ 30 x 1 ≤ 4 x 1 ≥ 2 x 1 ≥ 3 x 2 ≤ 3 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm min W = -x_1 -5 x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - x_2 \geq -2 \\\\ \rm 5x_1 + 6x_2 \leq 30 \\\\ \rm x_1 \leq 4 \\\\ \rm x_1 \geq 2 \\\\ \rm x_1 \geq 3 \\\\ \rm x_2 \leq 3 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} minW=−x1​−5x2​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​x1​−x2​≥−25x1​+6x2​≤30x1​≤4x1​≥2x1​≥3x2​≤3x1​,x2​≥0​​

求上述 L P 212 \rm LP212 LP212 分支的最优解 { x 1 = 3 x 2 = 2.5 \begin{cases} \rm x_1 =3 \\\\ \rm x_2 = 2.5 \end{cases} ⎩⎪⎨⎪⎧​x1​=3x2​=2.5​ , 将上述最优解代入约束方程 ,

得到整数规划最小值 m i n W = − x 1 − 5 x 2 = − 15.5 \rm min W = -x_1 -5 x_2 = - 15.5 minW=−x1​−5x2​=−15.5

定界 : L P 212 \rm LP212 LP212 分支的最优解不是整数 , 其目标值 − 15.5 - 15.5 −15.5 要比当前的界 − 17 -17 −17 要差 , 因此该分支直接裁减掉 ;

该整数规划 I P \rm IP IP 的最优解 { x 1 = 2 x 2 = 3 \begin{cases} \rm x_1 = 2 \\\\ \rm x_2 = 3 \end{cases} ⎩⎪⎨⎪⎧​x1​=2x2​=3​ , 将上述最优解代入约束方程 ,

得到整数规划最小值 m i n W = − x 1 − 5 x 2 = − 17 \rm min W = -x_1 -5 x_2 = - 17 minW=−x1​−5x2​=−17

分支记录如下 :