数学建模之插值与拟合(附实例及MATLAB源码) |
您所在的位置:网站首页 › 数学建模常用代码 › 数学建模之插值与拟合(附实例及MATLAB源码) |
数学建模之插值与拟合(附实例及MATLAB源码)
|
拟合和插值
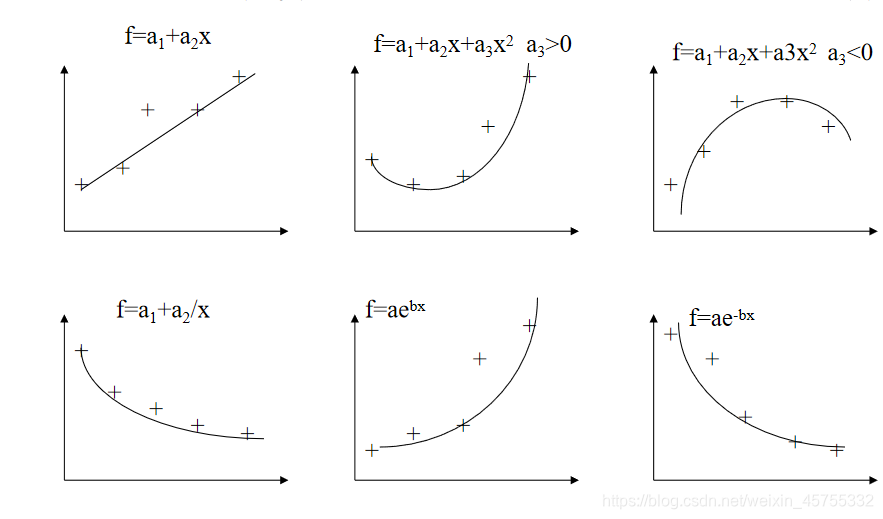
在实际中,常常要处理由实验或测量所得到的一些离散数据。插值与拟合方法就是要通过这些数据去确定某一类知函数的参数或寻求某个近似函数,使所得到的近似函数与E知数据有较高的拟合精度。 插值如果要求这个近似函数(曲线或曲面)经过所已知的所有数据点,则称此类问题为插值问题。(不需要函数 表达式) 拟合如果不要求近似函数通过所有数据点,而是要求它能较好地反映数据变化规律的近似函数的方法称为数据拟合。(必须有函数表达式),近似函数不一定(曲线或曲面)通过所有的数据点。(在这种情况下,通常要求观测数据相对比较准确,即不考虑观测误差的影响。) 插值和拟合的异同 (1)联系都是根据实际中一-组已知数据来构造一个能够反映数据变化规律的近似函数的方法。 (2)区别插值问题不一定得到近似函数的表达形式, 仅通过插值方法找到末知点对应的值。数据拟合要求得到一个具体的近似函数的表达式。 观测数据能否正确揭示某些变量之间的关系,往往取决于两个方面 其一是观测数据的准确性或准确程度,这是因为在获取观测数据的过程中一般存在随机测量误差,导致所讨论的变量成为随机变量。 其二是对观测数据处理方法的选择,即到底是采用插值方法还是用拟合方法,插值方法之中、拟合方法之中又选用哪一种插值或拟合技巧来处理观测数据。 数据拟合对于情况较复杂的实际问题(因素不易化简,作用机理不详)可直接使用数据组建模,寻找简单的因果变量之间的数量关系,从而对未知的情形作预报。这样组建的模型为拟合模型。拟合模型的组建主要是 处理好观测数据的误差,使用数学表达式从数量上近似因果变量之间的关系。拟合模型的组建是通过对有关变量的观测数据的观察、分析和选择恰当的数学表达方式得到的。 在科学计算中经常要根据给定函数的实验数据,需要用比较简单和合适的函数来逼近(或拟合)实验数据。这种逼近的特点是: (a) 适度的精度是需要的; (b) 实验数据有小的误差; © 对于某些问题,可能有某些特殊的信息能够用来选择实验数据的数学模型。 数据拟合基本方法 最小二乘法一函数表达式为 若记 一般先画出数据的散点图,通过散点图的大体形状来确定函数。 人们常用的曲线有 (1)直线
y
=
a
1
x
+
a
2
y=a_1x+a_2
y=a1x+a2 (2)多项式 (3)双曲线(一支)
y
=
a
1
x
+
a
2
y=\frac{a_1}{x}+a_2
y=xa1+a2 ,拟合前作变量 替换t=1/x,求解a1,a2较简单。 (4)指数曲线
y
=
a
1
e
a
2
x
y=a_1e^{a_2x}
y=a1ea2x,拟合前作变量代换,先两遍取对数,则
l
n
(
y
)
=
l
n
(
a
1
e
a
2
x
)
,
设
z
=
l
n
y
,
m
=
l
n
(
a
1
)
所
以
z
=
m
+
r
t
ln(y)=ln({a_1e^{a_2x}}),设z=lny,m=ln(a_1)所以z=m+rt
ln(y)=ln(a1ea2x),设z=lny,m=ln(a1)所以z=m+rt这样指数曲线转化为线性函数,求解a1,a2较简单。 语法 p = plotfit(x.y,n) 返回次数为n的多项式p(x)的系数,该阶数是y中数据的最佳拟合(在最小二乘方式中)。p中的系数按降幂排列,p的长度为n+1 多项式在x处的值y可用下面的函数计算 y=polyval(a,x) 示例: 1949年- -1994年我国人口数据资料如下: 年份xi1949195419591964196919741979198419891994人口数yi5.46.06.77.08.19.19.810.311.311.8建模分析我国人口增长的规律,预报1999年我国人口数。 clear; x= [1949 1954 1959 1964 1969 1974 1979 1984 1989 1994] ; y=[5.4 6.0 6.7 7.0 8.1 9.1 9.8 10.3 11.3 11.8 ]; x1=1949:10:1994; a=polyfit(x,y,1); y1=a(2)+a(1)*x1; %模型一 b=polyfit(x,log(y),1); y2=exp(b(2))*exp(b(1)*x1); %模型二 用exp是要将ln转化回去 plot(x,y,'*') hold on plot(x1,y1,'--r') hold on plot(x1,y2,'-k') legend('原曲线','模型一曲线','二曲线')在MATLAB工作区都是可以看到a(1),a(2)的值的,a(2)也就是下面的a,a(1)就是下面的b 非线性最小二乘法是假设f (x)是待定系数的任意非线性函数,在最小二乘准则下求其系数 a k a_k ak 例如常用的双曲线和指数曲线就是非线性最小二乘拟合中最常用的非线性函数,只不过在上面使用中将它们转变成线性最小二乘拟合方法。 例如当实验数据具有单调性和凸性时,可选择下述适当的数学模型y = f (x)来拟合实验数据。其中a、b 为参数。在有可能的情况下,一般将非线性拟合函数转化为线性拟合函数求解。
工作区中x的值为,分别代表 a b k 0.00694062292915721 -0.00293659350172876 0.0809312312491527 lsqnonlin函数 function f=curvefun2(x) tdata=100:100:1000; cdata=1e-03*[4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50,6.59]; f=x(1)+x(2)*exp(-0.02*x(3)*tdata)- cdata clc;clear; x0=[0.82,0.5,0.05]; x=lsqnonlin('curvefun2',x0) f= curvefun2(x) x 检验拟合好坏的标准
当数据量不够,需要补充,且认定已有数据可信时,通常利用函数插值方法。 实际问题当中碰到的函数f (X)是各种各样的,有的表达式很复杂,有的甚至给不出数学的式子,只提供了一些离散数据,让我们用这些离散数据来预测其他值。 插值方法在实际问题中所遇到的插值问题一般分为 一维插值问题和二维插值问题。 常见的有: (1)拉格朗日插值(lagrange插值) (2)分段线性插值 (3) Hermite (4)三次样条插值。 拉格朗日插值(高次多项式插值): 曲线光滑;误差估计有表达式收敛性不能保证(振荡现象)用于理论分析,实际意义不大分段线性插值: 收敛性良好只用两个节点,且线性,简单实用曲线不光滑三次样条插值:(*) 曲线2阶光滑,收敛性有保证实际中应用广泛误差估计较难常见的插值函数 函数说明interp1一维数据插值(表查找)interp2meshgrid格式的二维网格数据的插值interp3meshgrid格式的三维网格数据的插值griddata插入二维或三维散点数据
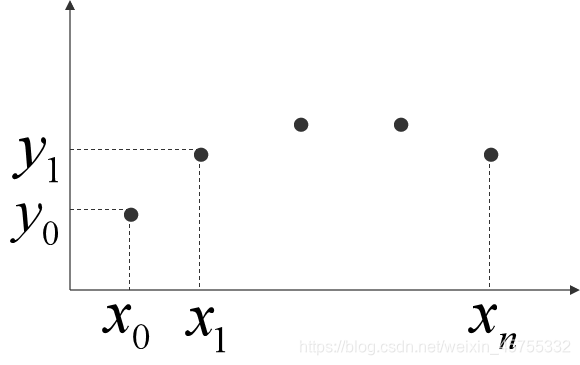
如图,有n+1个节点&(x_j,y_j),(j=0…n)&,这些节点是找不到某些函数来对其拟合,或者函数极为复杂,现在要求任意一点
x
k
x_k
xk的值
y
k
y_k
yk 已知函数f(x)在
n
+
1
n+1
n+1个点
x
0
,
x
1
,
…
,
x
n
x_0,x_1,…,x_n
x0,x1,…,xn 处的函数值为
y
0
,
y
1
,
…
,
y
n
y_0,y_1,…,y_n
y0,y1,…,yn。求一n次多项式函数Pn(x),使其满足
P
n
(
x
i
)
=
y
i
,
i
=
0
,
1
,
…
,
n
.
P_n(x_i)=y_i,i=0,1,…,n.
Pn(xi)=yi,i=0,1,…,n. 解决此问题的拉格朗日插值多项式公式为
P
n
(
x
)
=
∑
L
i
(
x
)
∗
y
i
P_n(x)=\sum{L_i(x)*y_i}
Pn(x)=∑Li(x)∗yi 其中
L
i
(
x
)
L_i(x)
Li(x)为n次多项式
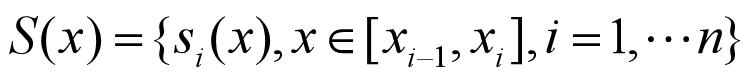
y i = i n t e r p 1 ( x , y , x i , ′ m e t h o d ′ ) yi=interp1(x,y,xi,'method') yi=interp1(x,y,xi,′method′) y i y_i yi: x i x_i xi处的插值结果x y 是插值节点 x i x_i xi是被插值点method是插值方法插值方法有: ‘nearest’ :最邻近插值 ‘linear’ : 线性插值; ‘spline’ : 三次样条插值; ‘cubic’ : 立方插值。 缺省时: 分段线性插值。 下面来看下这些方法的一些区别 注意:所有的插值方法都要求x是单调的,并且 x i x_i xi不能够超过x的范围 例:在1-12的11小时内,每隔1小时测量一次温度,测得的温度依次为:5,8,9,15,25,29,31,30,22,25,27,24。试估计每隔1/10小时的温度值。 clear hours=1:12; temps=[5 8 9 15 25 29 31 30 22 25 27 24]; h=1:0.1:12; t=interp1(hours,temps,h,'spline') t1=interp1(hours,temps,h,'line') plot(hours,temps,'+',h,t,'r :',h,t1,'b') legend('原值','三次样条','线性') xlabel('Hour'),ylabel('Degrees Celsius') t(1:10:100) t1(1:10:100)
5.3000 8.1000 9.6000 16.0000 25.4000 29.2000 30.9000 29.2000 22.3000 25.2000 例 已知飞机下轮廓线上数据如下,求x每改变0.1时的y值。 这里用了三种插值的方法 clear clc x0=[0 3 5 7 9 11 12 13 14 15 ]; y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6 ]; x=0:0.1:15; y1=lagr1(x0,y0,x); y2=interp1(x0,y0,x); y3=interp1(x0,y0,x,'spline'); subplot(3,1,1) plot(x0,y0,'*',x,y1,'r') grid title('lagrange') subplot(3,1,2) plot(x0,y0,'*',x,y2,'r') grid title('piecewise linear') subplot(3,1,3) plot(x0,y0,'*',x,y3,'r') grid title('spline') y1(1:10:150) y2(1:10:150) y3(1:10:150)
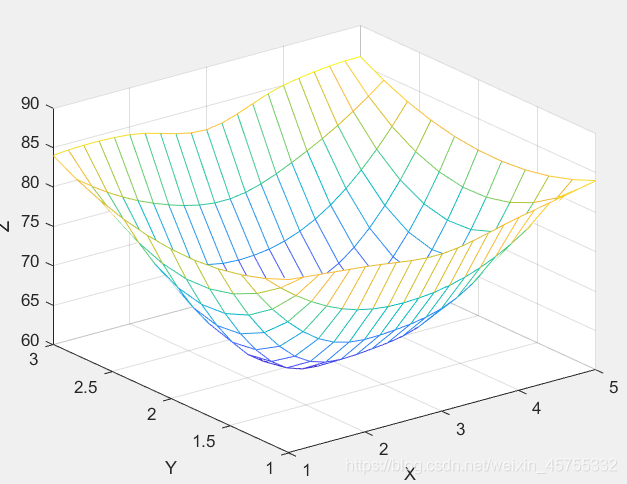
第一种(网格节点): z = i n t e r p 2 ( x 0 , y 0 , z 0 , x , y , ’ m e t h o d ’ ) z=interp2(x0,y0,z0,x,y,’method’) z=interp2(x0,y0,z0,x,y,’method’) z: 被插值点的函数值x0,y0,z0: 插值节点x,y : 被插值点mrthod 插值方法插值方法: ‘nearest’ 最邻近插值 ‘linear’ 双线性插值 ‘cubic’ 双三次插值 缺省时, 双线性插值 要求x0,y0单调;x,y可取为矩阵,或x取行向量,y取为列向量,x,y的值分别不能超出x0,y0的范围。 例:测得平板表面3*5网格点处的温度分别为: 82 81 80 82 84 79 63 61 65 81 84 84 82 85 86 试作出平板表面的温度分布曲面z=f(x,y)的图形。 注意interp2(x,y,temps,xi,yi’ )yi得转化为他的转置矩阵 yi’ 才行 x=1:5; y=1:3; temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86]; mesh(x,y,temps) pause(1.5) %暂停1.5秒继续运行 xi=1:0.2:5; yi=1:0.2:3; figure(2) z1i=interp2(x,y,temps,xi,yi','nearest'); %最近邻插值 mesh(xi,yi,z1i) xlabel('X'),ylabel('Y'),zlabel('Z') pause(1.5) figure(3) z2i=interp2(x,y,temps,xi,yi'); %双线性插值 mesh(xi,yi,z2i) xlabel('X'),ylabel('Y'),zlabel('Z') pause(1.5) figure(4) z3i=interp2(x,y,temps,xi,yi','cubic'); %双三次插值 mesh(xi,yi,z3i) xlabel('X'),ylabel('Y'),zlabel('Z')原图
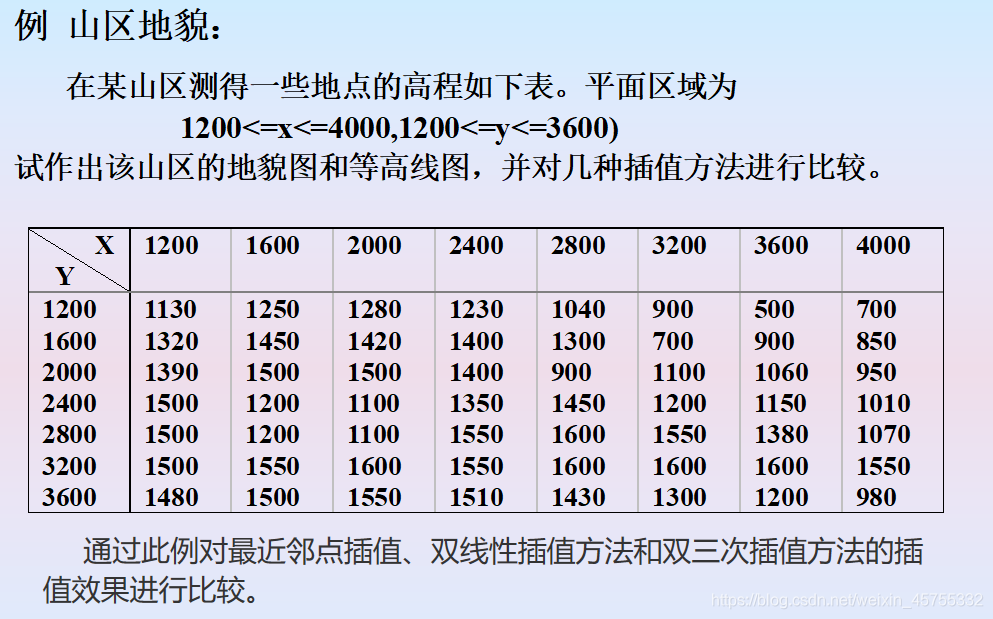
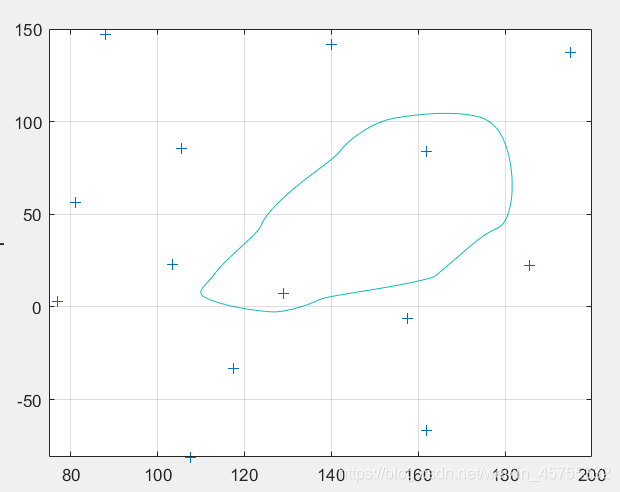
c z = g r i d d a t a ( x , y , z , c x , c y , ‘ m e t h o d ’ ) cz =griddata(x,y,z,cx,cy,‘method’) cz=griddata(x,y,z,cx,cy,‘method’) cz 被插值点的函数值x y z 是插值节点cx cy 是被插值点method是插值方法 要求cx取行向量,cy取为列向量。插值方法有: ‘nearest’ 最邻近插值 ‘linear’ 双线性插值 ‘cubic’ 双三次插值 ‘v4’- Matlab提供的插值方法 缺省时, 双线性插值
|
【本文地址】
今日新闻 |
推荐新闻 |
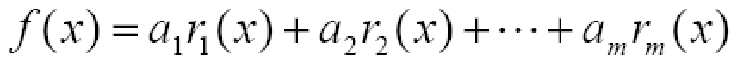 其中
r
k
(
x
)
,
k
=
1
:
m
r_k(x),k=1:m
rk(x),k=1:m 是一组事先选定的线性无关的函数,
a
k
a_k
ak 是一组待定系数。寻求系数
a
k
a_k
ak 使得
y
i
y_i
yi 与
f
(
x
i
)
f(x_i)
f(xi) 的距离 的平方和最小。这种准则称为最小二乘准则,其求系数的方法称为线性最小二乘拟合方法。
其中
r
k
(
x
)
,
k
=
1
:
m
r_k(x),k=1:m
rk(x),k=1:m 是一组事先选定的线性无关的函数,
a
k
a_k
ak 是一组待定系数。寻求系数
a
k
a_k
ak 使得
y
i
y_i
yi 与
f
(
x
i
)
f(x_i)
f(xi) 的距离 的平方和最小。这种准则称为最小二乘准则,其求系数的方法称为线性最小二乘拟合方法。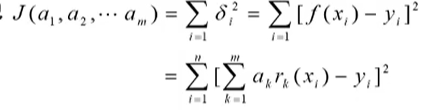 问题归结为,求
a
k
,
(
k
=
1...
m
)
a_k ,(k=1...m)
ak,(k=1...m)使得J最小 具体怎么弄 不推导,会用就行MATLAB就行,来直接看例子吧。
问题归结为,求
a
k
,
(
k
=
1...
m
)
a_k ,(k=1...m)
ak,(k=1...m)使得J最小 具体怎么弄 不推导,会用就行MATLAB就行,来直接看例子吧。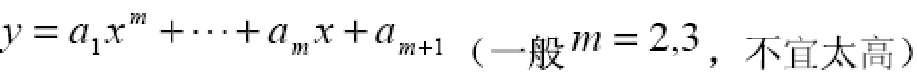


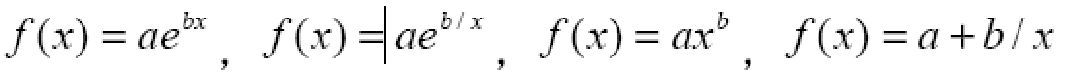 Matlab的提供了两个求非线性最小二乘拟合的函数:lsqcurvefit和lsqnonlin。两个命令都要先建立M-文件fun.m,在其中定义函数f(x),但两者定义f(x)的方式是不同的,可参考例题. 用下面一组数据拟合 函数
c
(
t
)
=
a
+
b
−
0.02
k
t
c(t)=a+b^{-0.02kt}
c(t)=a+b−0.02kt 中的参数a,b,k
Matlab的提供了两个求非线性最小二乘拟合的函数:lsqcurvefit和lsqnonlin。两个命令都要先建立M-文件fun.m,在其中定义函数f(x),但两者定义f(x)的方式是不同的,可参考例题. 用下面一组数据拟合 函数
c
(
t
)
=
a
+
b
−
0.02
k
t
c(t)=a+b^{-0.02kt}
c(t)=a+b−0.02kt 中的参数a,b,k 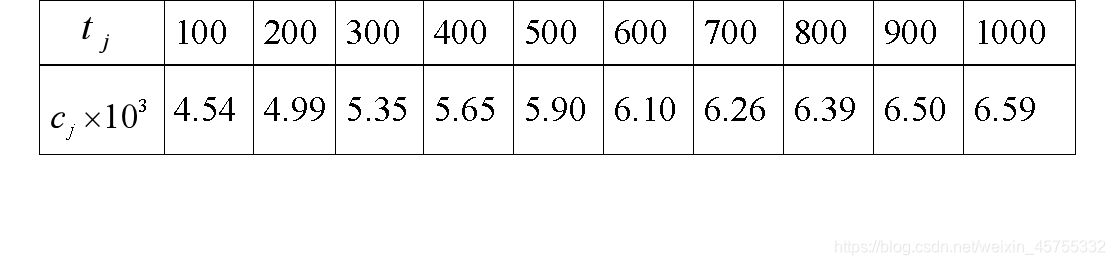 该问题就是求最优解
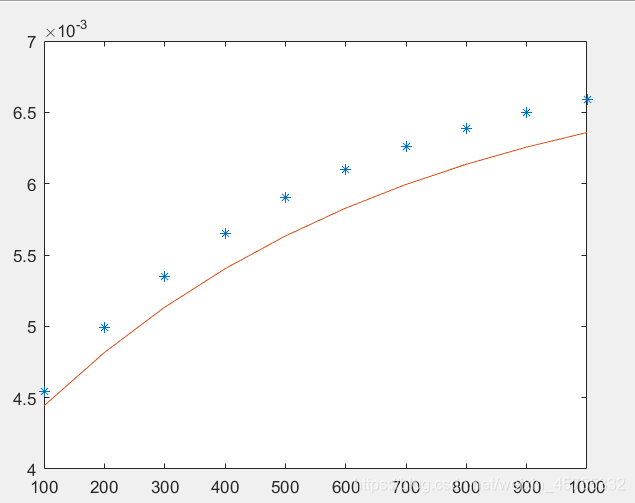
该问题就是求最优解 
 R
2
R^2
R2是一个统计量,其值在(0,1)之间,越大越好,平方和越小越好。
R
2
R^2
R2是一个统计量,其值在(0,1)之间,越大越好,平方和越小越好。
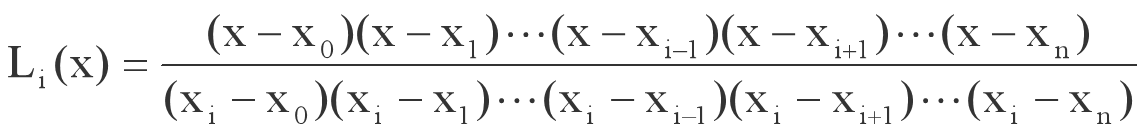 称为拉格朗日插值基函数 如两点一次(线性)插值多项式:
称为拉格朗日插值基函数 如两点一次(线性)插值多项式: 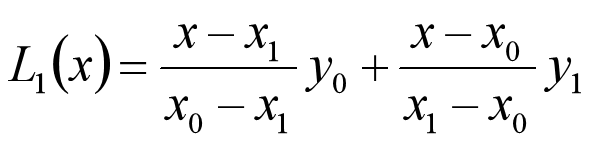 三点二次(抛物)插值多项式:
三点二次(抛物)插值多项式: 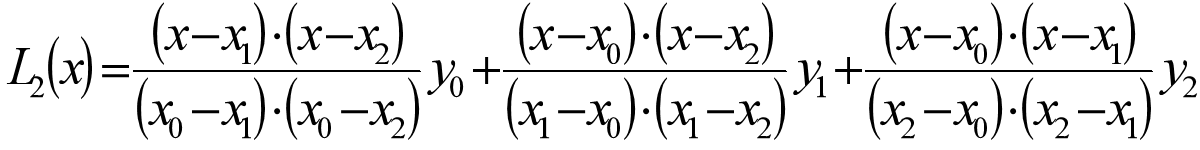
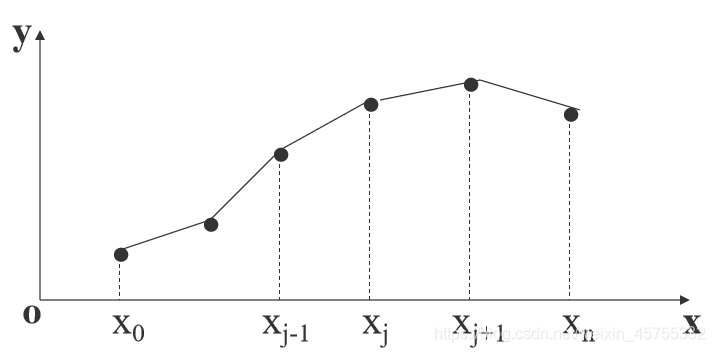
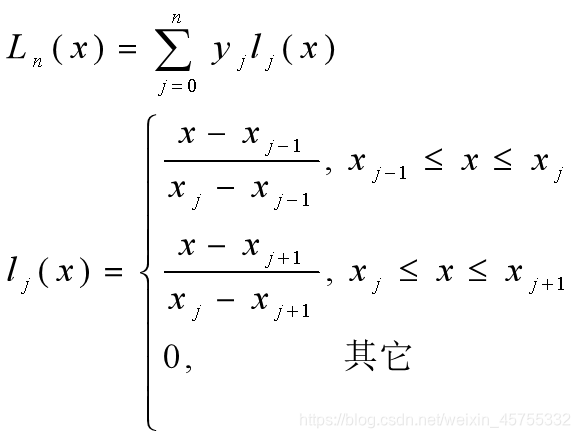 计算量与n无关; n越大,误差越小.
计算量与n无关; n越大,误差越小.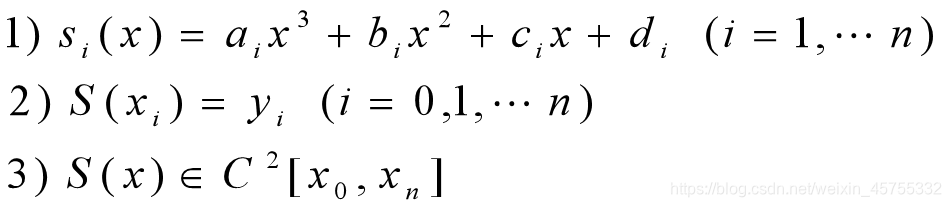
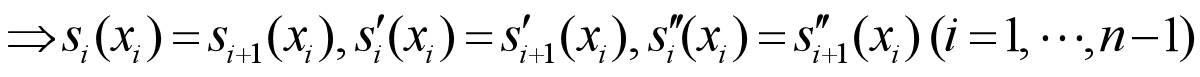
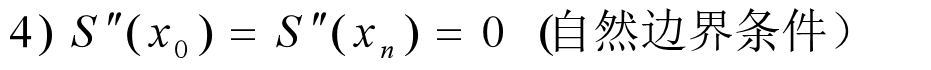
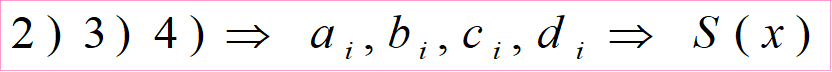
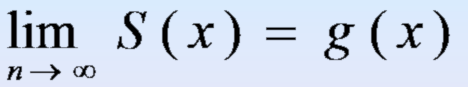 g(x)为被插值函数。
g(x)为被插值函数。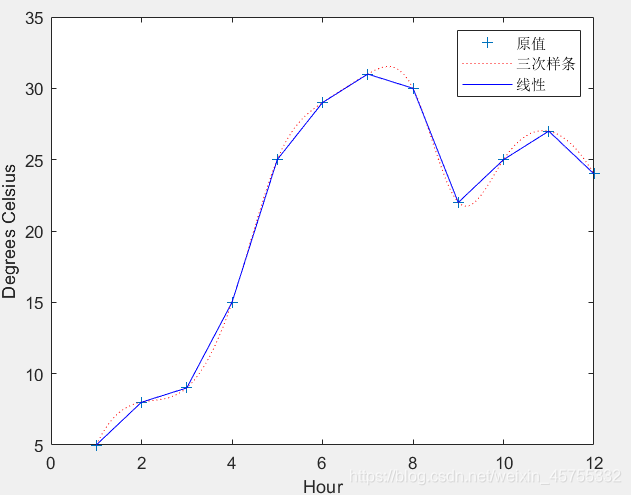 这只输出了每隔一小时测量的温度 5.6242 8.0544 9.3052 15.9739 25.7091 29.2136 31.1755 29.2905 21.7705 25.4456
这只输出了每隔一小时测量的温度 5.6242 8.0544 9.3052 15.9739 25.7091 29.2136 31.1755 29.2905 21.7705 25.4456
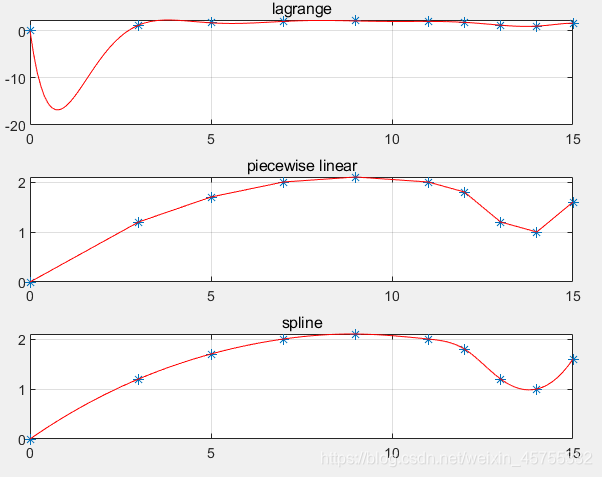 y1(1:10:150) 0 -15.9238 -5.4272 1.2000 2.2666 1.7000 1.6249 2.0000 2.2040 2.1000 1.9904 2.0000 1.8000 1.2000 1.0000 y2(1:10:150) 0 0.4000 0.8000 1.2000 1.4500 1.7000 1.8500 2.0000 2.0500 2.1000 2.0500 2.0000 1.8000 1.2000 1.0000 y3(1:10:150) 0 0.4665 0.8649 1.2000 1.4767 1.7000 1.8740 2.0000 2.0773 2.1000 2.0668 2.0000 1.8000 1.2000 1.0000
y1(1:10:150) 0 -15.9238 -5.4272 1.2000 2.2666 1.7000 1.6249 2.0000 2.2040 2.1000 1.9904 2.0000 1.8000 1.2000 1.0000 y2(1:10:150) 0 0.4000 0.8000 1.2000 1.4500 1.7000 1.8500 2.0000 2.0500 2.1000 2.0500 2.0000 1.8000 1.2000 1.0000 y3(1:10:150) 0 0.4665 0.8649 1.2000 1.4767 1.7000 1.8740 2.0000 2.0773 2.1000 2.0668 2.0000 1.8000 1.2000 1.0000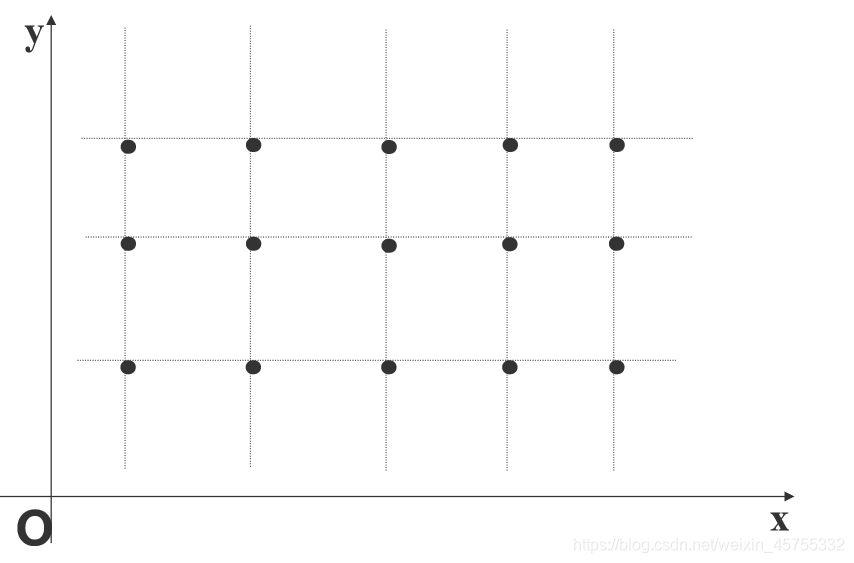 第二种(散乱节点):
第二种(散乱节点): 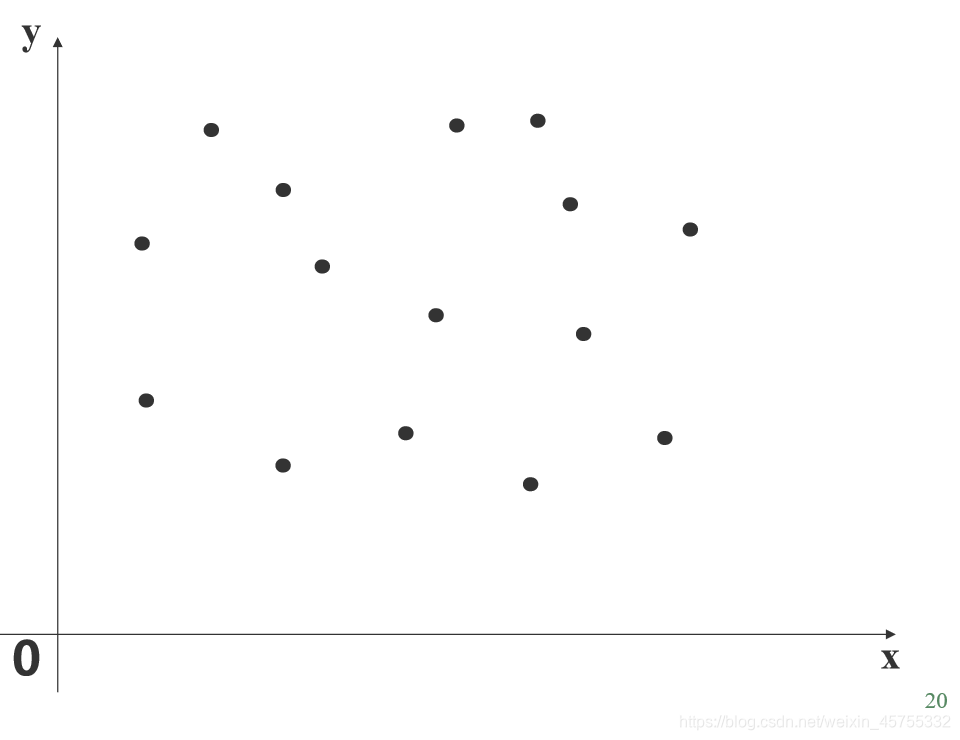
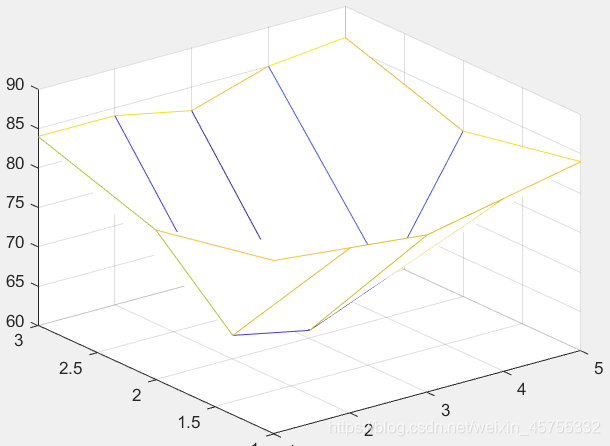 最近邻插值
最近邻插值 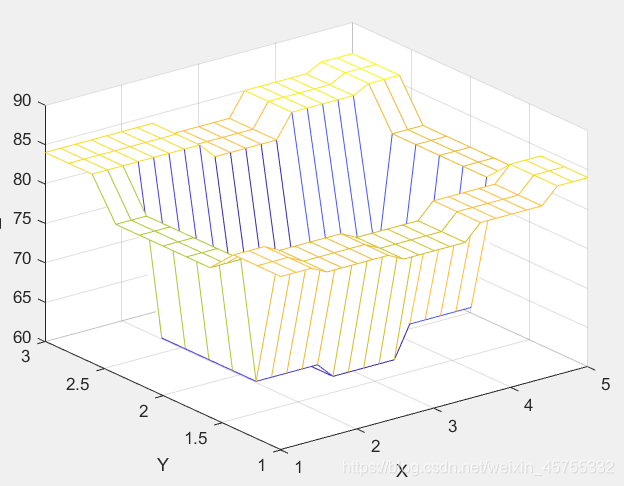 双线性插值
双线性插值 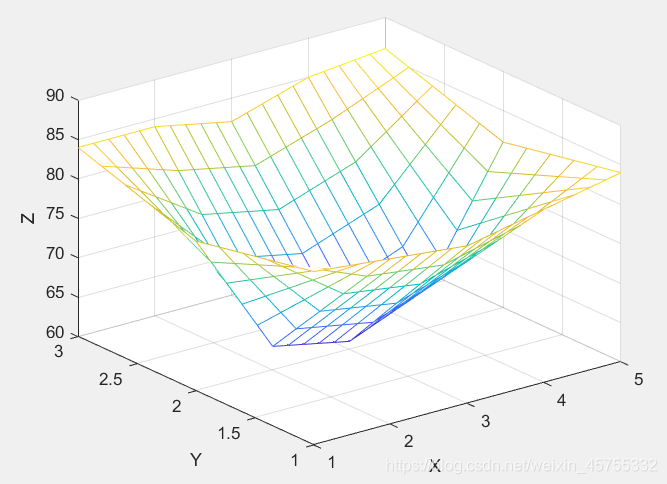 双三次插值
双三次插值