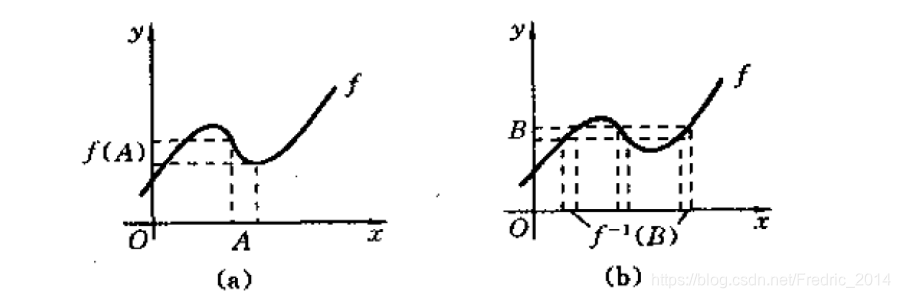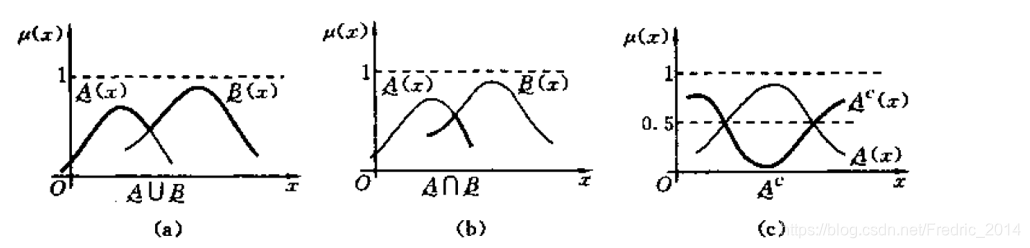【参考资料】 【1】《模糊数学方法及其应用》

定义: 设 A ∈ F ( U ) A \in F(U) A∈F(U)，U是论域（论域相当于全集），具有如下性质: X A : U → ( 0 , 1 ) X_A:U \to (0, 1) XA​:U→(0,1)

x → X A ( x ) = { 1 , x ∈ A 0 , x ∉ A x \to X_A(x)= \begin{cases} 1, ; x \in A \\ 0, ; x \notin A \end{cases} x→XA​(x)={1,0,​x∈Ax∈/​A​ 备注：经典集合逻辑上可以表示为一个映射，属于集合能映射到1，否则映射到0

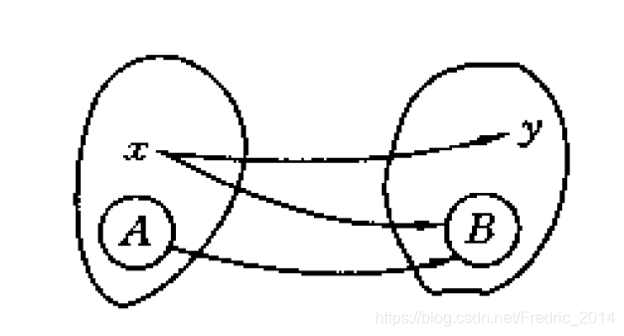
定义: 设 f : X → Y f:X \to Y f:X→Y,则称映射 f : X → F ( Y ) f:X \to F(Y) f:X→F(Y)为x到y的点-集映射。

定义: 设 T : X → Y T:X \to Y T:X→Y,称这个映射为集合变换。

经典的函数映射为点-点映射，即上图中的x到y，而通常还有问题需要点-集映射，如x到集合B，以及集合到集合的映射，如A到B。

经典扩张原理:

设映射 f : X → Y , x ⟼ f ( x ) = y , ∀ A ∈ F ( X ) f:X \to Y, x \longmapsto f(x)=y,\forall A \in F(X) f:X→Y,x⟼f(x)=y,∀A∈F(X)，令 f ( A ) = { y ∈ Y ∣ y = f ( x ) , x ∈ A } f(A)=\{ y \in Y|y=f(x), x \in A \} f(A)={y∈Y∣y=f(x),x∈A}，则集合 f ( A ) ∈ F ( Y ) f(A) \in F(Y) f(A)∈F(Y)称为集合A在f下的像；对于 ∀ B ∈ F ( Y ) \forall B \in F(Y) ∀B∈F(Y)，令 f − 1 ( B ) = { x ∣ x ∈ X ∣ f ( x ) ∈ B } f^{-1}(B)=\{x|x \in X|f(x) \in B\} f−1(B)={x∣x∈X∣f(x)∈B}，则集合 f ( B ) ∈ F ( X ) f(B) \in F(X) f(B)∈F(X)为B在f下的原像。

备注：这里的经典扩张原理实际上是一个定义，将原来经典集合论下点到点的函数定义扩展为集合到集合。如下图所示:

a. 等价关系

定义: 若集合X上的二元关系R具有自反性、对称性和传递性，则称R是X上的一个等价关系。

这个定义在抽象代数里有提过，等价关系代表着集合里的一个等价类划分。 例如年龄相同是一个等价类，它把同学按照不同的年龄划分群体。

b. 相似关系 定义: 若集合X上的二元关系R具有自反性、对称性，则称R是X上的一个相似关系。

相似关系不具备传递性，例如朋友关系、同学关系，举例如下:

从相似类划分可以看到，实际上在相似矩阵里代表着一个全1的矩阵，能够互相转换。

定义：设集合L中规定了两种运算 ∨ \lor ∨和 ∧ \land ∧，即 a ∨ b = s u p { a , b } a \lor b = sup\{a, b\} a∨b=sup{a,b}， a ∧ b = i n f { a , b } a \land b = inf\{a, b\} a∧b=inf{a,b}，并且满足如下性质: 幂等律: a ∨ a = a , a ∧ a = a a \lor a = a, \quad a \land a = a a∨a=a,a∧a=a 交换律: a ∨ b = b ∨ a , a ∧ b = b ∧ a a \lor b = b \lor a, \quad a \land b = b \land a a∨b=b∨a,a∧b=b∧a 结合律: ( a ∨ b ) ∨ c = a ∨ ( b ∨ c ) , ( a ∧ b ) ∧ c = a ∧ ( b ∧ c ) (a \lor b) \lor c = a \lor (b \lor c), (a \land b) \land c = a \land (b \land c) (a∨b)∨c=a∨(b∨c),(a∧b)∧c=a∧(b∧c) 吸收律: ( a ∨ b ) ∧ a = a , ( a ∧ b ) ∨ a = a (a \lor b) \land a = a, (a \land b) \lor a = a (a∨b)∧a=a,(a∧b)∨a=a 则称L是一个格，记作 ( L , ∨ , ∧ ) (L, \lor, \land) (L,∨,∧)

这里从经典集合论的特征函数衍生出去，对于经典特征函数，其映射非0即1，代表某个元素要么属于这个集合，要么不属于这个集合。而模糊子集是一个模糊的概率，其特征函数是一个0到1的闭集，可以理解为有多少概率属于某个集合。

定义: 设U是论域，称映射 μ A : U → [ 0 , 1 ] , x ⟼ μ A ( x ) ∈ [ 0 , 1 ] \mu_A: U \to [0,1], x \longmapsto \mu_A(x) \in [0, 1] μA​:U→[0,1],x⟼μA​(x)∈[0,1]，确定了U上的一个模糊子集A，称 μ A \mu_A μA​为A的隶属函数， μ A ( x ) \mu_A(x) μA​(x)为x（这里可以这样理解: x是论域U中的一个点，A是U的一个子集）对A的隶属程度。若 μ A ( x ) = 0.5 \mu_A(x)=0.5 μA​(x)=0.5时，称该点为过渡点，此时最模糊。

举例:

论域 U = { x 1 , x 2 , . . . , x n } U=\{x_1,x_2, ..., x_n \} U={x1​,x2​,...,xn​}，对于U上的任意一个模糊集A,存在隶属函数 A ∼ ( x i ) i = ( 1 , 2 , 3 , . . . , n ) \underset{\sim}{A}(x_i) i=(1,2,3,...,n) ∼A​(xi​)i=(1,2,3,...,n),表示如下:

A ∼ = A ∼ ( x 1 ) x 1 + A ∼ ( x 2 ) x 2 + . . . + A ∼ ( x n ) x n \underset{\sim}{A} = \dfrac{\underset{\sim}{A}(x_1)}{x_1} + \dfrac{\underset{\sim}{A}(x_2)}{x_2} + ... + \dfrac{\underset{\sim}{A}(x_n)}{x_n} ∼A​=x1​∼A​(x1​)​+x2​∼A​(x2​)​+...+xn​∼A​(xn​)​

注意这里的分号、加号都只是一个符号表示，不是运算意义上的分号和加号。

序偶表示法 A ∼ = { ( x 1 , A ∼ ( x 1 ) ) , ( x 2 , A ∼ ( x 2 ) ) , . . . , ( x n , A ∼ ( x n ) ) } \underset{\sim}{A} = \{(x_1, \underset{\sim}{A}(x_1)), (x_2, \underset{\sim}{A}(x_2)),..., (x_n, \underset{\sim}{A}(x_n)) \} ∼A​={(x1​,∼A​(x1​)),(x2​,∼A​(x2​)),...,(xn​,∼A​(xn​))}

向量表示法 A ∼ = { A ∼ ( x 1 ) , A ∼ ( x 2 ) , . . . , A ∼ ( x n ) } \underset{\sim}{A} = \{\underset{\sim}{A}(x_1), \underset{\sim}{A}(x_2),..., \underset{\sim}{A}(x_n) \} ∼A​={∼A​(x1​),∼A​(x2​),...,∼A​(xn​)}

并 : ( A ∼ ∪ B ∼ ) ( x ) ⇒ A ∼ ( x ) ∨ B ∼ ( x ) , ∀ x ∈ U (\underset{\sim}{A} \cup \underset{\sim}{B})(x) \Rightarrow \underset{\sim}{A}(x) \lor \underset{\sim}{B}(x), \forall x \in U (∼A​∪∼B​)(x)⇒∼A​(x)∨∼B​(x),∀x∈U

交 : ( A ∼ ∩ B ∼ ) ( x ) ⇒ A ∼ ( x ) ∧ B ∼ ( x ) , ∀ x ∈ U (\underset{\sim}{A} \cap \underset{\sim}{B})(x) \Rightarrow \underset{\sim}{A}(x) \land \underset{\sim}{B}(x), \forall x \in U (∼A​∩∼B​)(x)⇒∼A​(x)∧∼B​(x),∀x∈U

余 : A ∼ ( x ) C ⇒ 1 − A ∼ ( x ) \underset{\sim}{A}(x)^C \Rightarrow 1- \underset{\sim}{A}(x) ∼A​(x)C⇒1−∼A​(x)

图例:

图例看不清，加几句备注。图a取交集等于取隶属函数A和B中的大值，可以看到上面那条线粗一点；图b取并集等于取隶属函数A和B中的小值，可以看到下面那条线粗一点；图c取余集等于每次用1减去当前的隶属函数值。

定义: 设 A ∼ ∈ F ( U ) \underset{\sim}{A} \in F(U) ∼A​∈F(U)，对于 ∀ γ ∈ [ 0 , 1 ] \forall \gamma \in [0,1] ∀γ∈[0,1],记作： A γ = { x ∣ A ∼ ( x ) ≥ γ } A_{\gamma} = \{x|\underset{\sim}{A}(x) \ge \gamma \} Aγ​={x∣∼A​(x)≥γ}。

简单讲就是把隶属函数大于某一个值得元素找出来，它表述对模糊度（可信度）的一种筛选，即低于某个阈值则剔除。

定义：数 λ \lambda λ（属于[0,1]）与模糊集 A ∼ \underset{\sim}{A} ∼A​的乘积为 λ ∧ A ∼ ( x ) \lambda \land \underset{\sim}{A}(x) λ∧∼A​(x)。

分解定理： 设 A ∼ ∈ F ( U ) \underset{\sim}{A} \in F(U) ∼A​∈F(U)，则 A ∼ = ∪ λ ∈ [ 0 , 1 ] λ A λ \underset{\sim}{A} = \underset{\lambda \in [0,1]}{\cup} \lambda A_{\lambda} ∼A​=λ∈[0,1]∪​λAλ​

上述分解定理表示一个模糊集可以分解成几个 λ \lambda λ及其截集的数乘。举例如下:

根据之前的经典扩展原理我们定义了一个集合到另外一个集合的映射。那么这个集合里的一个模糊子集在此映射下会产生什么样的模糊子集，就是扩张原理要表述的问题。

定义: 设映射 f : U → V f:U \to V f:U→V，称映射 f : F ( U ) → F ( V ) f:F(U) \to F(V) f:F(U)→F(V), A ∼ → f ( A ∼ ) \underset{\sim}{A} \to f(\underset{\sim}{A}) ∼A​→f(∼A​) 为映射f扩张的模糊变换，其隶属函数 f ( A ∼ ) ( v ) = ∨ f ( u ) = v A ∼ ) ( u ) f(\underset{\sim}{A})(v) = \underset{f(u)=v}{\lor} \underset{\sim}{A})(u) f(∼A​)(v)=f(u)=v∨​∼A​)(u)

举例：