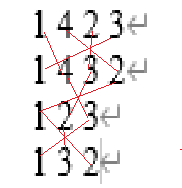
目录

一 互换与轮换

二 置换交换律与结合律

三 置换的化简方法

四 轮换的乘方计算方法

五 轮换的其他规律

六 置换凯来图

七 置换代数运算

       要了解群论，置换必不可少。而且置换在生活、工作中也非常常见。虽然说置换，有点小儿科，但是确实是数学里的重要内容。排列、组合和置换三者缺一不可。不能只学排列组合而不学置换。置换是对集合上的元素进行位置互换。这是对现实世界各种位置互换的抽象。现实中有很多置换的例子，比如击鼓传花游戏、华容道、滑块游戏、魔方、推箱子游戏、工厂的传送带、流水线等等。但是有些游戏，不是置换，比如象棋的吃子，就是替换，不是置换，那就是另一类数学问题。置换与排列密不可分。

       简单的置换分为两种：互换与轮换。

       同样，由简单到复杂。先由1 2 3 4 四个数字开始。

       首先是两两互换，所以这是个C(4,2)组合，所以有6种互换,如下

       1、2互换，1、3互换，1、4互换， 2、3互换， 2、4互换 ，3、4互换

       上面六个式子里的数字代表位置。

       轮换呢，就是几个位置，首位相连，形成一个环，每个位置把自身的元素移动到下一个位置。比如1、2、3轮换就是位置1上的元素移动到了位置2，位置2的元素移动到了位置3，位置3的元素移到了位置1。这对应了数学里循环排列的概念。互换其实是最小的轮换。所以，所有的置换都可以表示为轮换或轮换的组合，这个划重点记哈，是学习置换的基础。但是还有一类置换，就是什么都不改变，类似数字的0，叫恒等置换。

       因为置换的作用对象是某个排列，所以可以说置换是个一元运算符，也可以说置换是一个函数，也可以说置换是一个映射，也可以说置换是一种作用。

       置换怎么表示呢？

       如果用(1,2)这样的写法来表示置换，容易和线性代数里的向量搞混了，所以不能那么表示，标准的做法是空格隔开位置，外面加一对括号，然后数字代表位置。所以互换的写法如下：

       (1 2)  、(1 3)、  (1 4)、  (2 3) 、  (2 4)、  (3 4)

       多个元素的轮换，比如1、2、3的轮换记为(1 2 3)。当然，(1 2 3)也可以写(2 3 1)，因为1、2、3这3个顺序首位相连，形成一个环，以谁开始都无所谓。但是要注意里面不能有重复的位置，比如(1 2 1 4)这种就是不合法的置换，因为出现了1，2和1，4，这就有歧义了，位置1上的元素到底是移动到位置2，还是位置4呢？

       再考虑更复杂的置换的组合的写法

       比如(1 2)接着(1 3)怎么表示呢？

       群论里可以用加号+，也可以用乘号*，点号·，来表示“接着做”这个二元运算。伽罗瓦是推荐用乘号的，为了致敬伽罗瓦，我也用乘号，也可以省略乘号。而写的顺序就是按操作或执行顺序写

       所以(1 2)接着(1 3)写成(1 2)·(1 3)或 (1 2)(1 3)

       因为用的是乘号表达，所以(1 2 3)，再(1 2 3)就可以表示为二次方，就写成(1 2 3)2。

       那么反向轮换，就可以表示为-1次方，就写成(1 2 3)-1

       为了简洁，写轮换时，最好将最小的数字写在第一个位置。

       置换作用在排列上就直接把置换当成一个特殊函数，用函数的写法就行，比如对[A,B, C, D]这个字母的排列进行1、2、3轮换就可以这样写

       [A,B ,C ,D](1 2 3)=[C,A,B,D]

       注意：数学里{}表示集合，是没有顺序的，而[]表示排列（计算机界叫列表），是有顺序的。排列写前面，置换写后面意思是对排列进行置换。

       按照伽罗瓦的习惯，什么都不改变记为单位元e。

       可以做个小练习

       1 计算如下置换

       [精,忠,报,国](1 4 2 3)

       答案是[报,国,忠,精]

       2 原排列是[国,精,忠,报]，目前状态是[精,忠 ,报, 国],置换表达式是什么

       答案是(1 4 3 2)

       思考题：

       能不能用置换表示一个排列？

       答案：不能，除非指定初始排列。指定了初始状态的置换才能表示一个排列。

       那么继续探索置换是否符合交换律。

       以置换(1 3) (1 2)作用于(1 2 3 4)这个排列为例子：

       [1,2,3,4] (1 3)= [3, 2, 1, 4]

       ∴ [1, 2, 3, 4](1 3)(1 2)=[3, 2 ,1 ,4](1 2)=[2 ,3 ,1 ,4]

       注意，因为计算顺序是先计算(1 3)，再计算(1 2)，所以写法是 [1 ,2 ,3 ,4](1 3) (1 2) ，实际上要先计算[1 ,2, 3, 4](1 3) ，得到结果再执行(1 2)。

       而[2 ,3 ,1 ,4]是(1 3 2)这个轮换作用于[1 ,2 ,3, 4]这个排列的结果，所以(1 3) (1 2) = (1 3 2)。

       而经过运算我们得知，(1 2)(1 3)=(1 2 3)≠(1 3 2),所以置换不符合交换律

       再来看，无共同位置的置换叠加，也就是类似这种

       (1 2) (3 4)

       而这种置换是符合交换律的，因为两次置换互相独立。只有部分场景符合交换律，不能说置换这个运算符合交换律。

       那么置换符不符合结合律？

       肯定是符合的，因为假设有三次置换。先做前两次置换的组合运算，再做第三次置换。先做第一次置换，再做后两次置换的组合，效果都是顺序三次置换。

       正因为这样才有了置换的化简。

       首先可以把置换进行以下的分类，大类是三类e、轮换和轮换组合。

e

什么都不做，也叫恒等置换

轮换

互换

两个以上的元素轮换

轮换组合

各组之间没有相同位置、符合交换律,所以各组轮换的顺序可以任意调整

各组之间存在相同位置，不符合交换律，所以在写法上不能调整轮换的顺序

       置换的化简就是把轮换组合变成互相独立的轮换组合。这样做的目的是为了更方便计算，比如下面这个置换：

       (1 4 2 3)· (1 4 3 2) ·(1 2 3)·(1 3 2)

       这就非常复杂，让人根本不知道进行了什么。

       实际执行之后，和以下的置换结果是一样的

       (1 3 4)

       所以可以写成

       (1 4 2 3)· (1 4 3 2) ·(1 2 3)·(1 3 2)= (1 3 4)

       那么怎么化简啊？

       其实很简单，但是要仔细。以上面的式子为例子：

       首先看，1、2、3、4 四个位置都参与了置换

       就一个个来，首先看位置1

       (1 4 2 3) 位置1移动到了位置4

       (1 4 3 2) 位置4移动到了位置3

       (1 2 3)位置3移动到了位置1

       (1 3 2)位置1移动到了位置3

       所以最终位置1移动到了位置3

       再看位置2

       (1 4 2 3) 位置2移动到了位置3

       (1 4 3 2) 位置3移动到了位置2

       (1 2 3)位置2移动到了位置3

       (1 3 2)位置3移动到了位置2

       所以最终位置2不改变

       再看位置3

       (1 4 2 3) 位置3移动到了位置1

       (1 4 3 2) 位置1移动到了位置4

       (1 2 3)和(1 3 2)不影响位置4

       所以最终位置3移动到了位置4

       再看位置4

       (1 4 2 3) 位置4移动到了位置2

       (1 4 3 2) 位置2移动到了位置1

       (1 2 3)位置1移动到了位置2

       (1 3 2)位置2移动到了位置1

       所以最终结果是：

       位置1移动到了位置3

       位置2不改变

       位置3移动到了位置4

       位置4移动到了位置1

       那么最终化简之后，就是(1 3 4)

       总结一下，就是以下几步：

       1 找出所有发生改变的位置

       2 对每个位置，从第一个轮换开始，到最后一个轮换结束，跟踪变化，记录最终位置

       3 将起始位置和最终位置变成置换表达式

       学废了吗？

       化简后的置换表达式，如果是轮换组合，则这些组合是无关联的。

       上面的计算方法很繁琐，我推荐一个矩阵连线法手动计算非常方便快捷。这个手动计算方法来自国内一本介绍李群的电子书。还是刚刚的例子：

       (1 4 2 3)· (1 4 3 2) ·(1 2 3)·(1 3 2)

       写出一个矩阵(严格来讲不能叫矩阵，因为矩阵不能残缺啊，哈哈)

       1 4 2 3

       1 4 3 2

       1 2 3

       1 3 2

       再连线

       每个数字去连接下面行的下一个位置，但是不要忘了最后一行的计算

       所以有

       1 连线到1，再下一个位置为3

       3连线到1，再下一个位置为4

       4连线到2，再下一个位置1

       2连线到3，再下一个位置为2，不变

       所以结果为(1 3 4)

       所谓乘方，就是同样的轮换，重复几次

我可以用图形来表示，下图是轮换(1 2 3 4 5 6 7 8)前的状态

       这个图是轮换后的状态

       嗨，就是轮换一次转了1/8个圆周呗。转8次就转回原来位置呗。所以理解轮换，就是脑中想象一个圆盘，形成一个轮，然后就豁然开朗。

       根据上面介绍的化简方法，计算轮换的乘方，就非常简单了。

       比如这个复杂的轮换

       (1 11 4 2 3 8 5 12 6 10 7 9)

       重复9次结果为

       (1 10 5 2)·(3 11 7 12)·(4 9 6 8)

       那是怎么计算出来的呢？

       先把轮换表达式里的数字进行编号，也就是写出位置的索引

索引

1

2

3

4

5

6

7

8

9

10

11

12

位置

1

11

4

2

3

8

5

12

6

10

7

9

       以位置1为例子，轮换1轮，到了位置11，轮换二轮到了位置14，依此类推，第9轮就到了位置10。

       所以可以先对索引做加法

1

2

3

4

5

6

7

9

9

10

11

12

10

11

12

13

14

15

16

17

18

19

20

21

       那么这个索引超出了12，因为是轮换，形成一个轮，那么就需要取余数

       于是下面是取余结果，这就是新旧索引变化表

1

2

3

4

5

6

7

8

9

10

11

12

10

11

12

1

2

3

4

5

6

7

8

9

       然后再去原索引表找位置，记录变换后的位置

原位置

1

11

4

2

3

8

5

12

6

10

7

9

原索引

1

2

3

4

5

6

7

8

9

10

11

12

新索引

10

11

12

1

2

3

4

5

6

7

8

9

新位置

10

7

9

1

11

4

2

3

8

5

12

6

       删掉中间两行，得到位置变化表

原位置

1

11

4

2

3

8

5

12

6

10

7

9

新位置

10

7

9

1

11

4

2

3

8

5

12

6

       所以置换表达式为

(1 10 5 2)(3 11 7 12) (4 9 6 8)

       故(1 11 4 2 3 8 5 12 6 10 7 9)9= (1 10 5 2) (3 11 7 12)(4 9 6 8)

所以计算方法如下：

1 写下置换表达式各个位置的索引表

2 根据轮换次数，按模加法（先加再取余数），得到新索引

3 根据新索引，按索引表取新位置记录下来，得到新旧位置变化表

4 根据新旧位置变化表写出新的置换表达式

由此，可以得到三个轮换幂运算的三个规律

规律一：N个位置的轮换重复N次回到初始状态（常识哈，无需证明）

脑中想象一个轮在转，转一圈，刚好是N次。

规律二：N个位置轮换i轮，结果是互相独立的gcd(i,n)组轮换，gcd是最大公约数的意思。

规律三：轮换的逆运算是其表达式里位置的倒序

逆运算，写法上就是-1次方。从排列A到排列B，置换是M，从排列B再回到排列A，置换就是M-1.

我们之所以大量研究轮换，无非是一点，轮换太重要了，在置换里占比太多了。先思考一个问题，我们都知道，置换就是三类：零置换、轮换组合、轮换。互换是最小的轮换，不单独考虑。

规律四：多个位置与同一个位置的置换形成轮换

(a b) (a c)(a d)……(a n)=(a b c d……n)

根据置换的化简规则，依次分析

a 位置到b，后面的表达式里没有了b

b位置到了a，第二个表达式里位置再到c

c位置到了a，下一个表达式里到了d，以后再无改变

此后，每个位置的改变都只出现在两个表达式中

最后一个元素n，位置到了a

所以形成了一个a到n的轮换

这个规律特别重要，可以快捷运算很多式子

由这个规律可以计算互换与轮换的乘法

比如下面这两个式子：

(1 2 3 4 5 6 7 8 9)·(5 6)=(1 2 3 4 6 7 8 9)

(5 6)·(1 2 3 4 5 6 7 8 9)=(1 2 3 4 5 7 8 9)

先分析第一个式子，其实就是对轮换的分解

(1 2 3 4 5 6 7 8 9)= (6 7 8 9 1 2 3 4 5)=

(6 7) (6 8) (6 9) (6 1) (6 2) (6 3) (6 4)  (6,5)

∴(1 2 3 4 5 6 7 8 9)(5,6)= (6 7) (6 8) (6 9) (6 1) (6 2) (6 3) (6 4) (6 5) (5 6)

= (6 7) (6 8) (6 9) (6 1) (6 2) (6 3) (6 4)

=(6 7 8 9 1 2 3 4)

=(1 2 3 4 6 7 8 9)

第二个式子，也是对轮换的分解

(1 2 3 4 5 6 7 8 9)= (5 6 7 8 9 1 2 3 4)

=(5 6) (5 7) (5 8) (5 9) (5 1) (5 2) (5 3) (5 4)

(5 6)·(1 2 3 4 5 6 7 8 9)= (5 6) (5 6) (5 7) (5 8) (5 9) (5 1) (5 2) (5 3) (5 4)

= (5 7) (5 8) (5 9) (5 1) (5 2) (5 3) (5 4)

=(5 7 8 9 1 2 3 4)

=(1 2 3 4 5 7 8 9)

规律五：类似以下这种链式置换，结果是顺序轮换的逆运算。

(a b)(b c)(c d)(d e)(e f)(f g)(g h)= (h g f e d c b a)

这个规律很容易明白。

A 会一直下去，到达h的位置

B 到a的位置，后续互换a再也不出现

C到了b的位置，后续互换b再也不出现

……

中间过程省略

一直到最后h互换到了g的位置。

所以组成了一个倒转的轮换。

规律六：所有的互换都可以拆分为第一个元素和其他元素的置换。因为(a b)(a c)(a b)= (b c)

这里b、c的互换，可以通过a为中介做的，这也是凯来图的基础。以四个元素的置换为例子，我们知道所有的24种排列对应24种置换（包括零置换e）。最基础的互换是以下六种

(1 2) (1 3) (1 4) (2 3)  (2 4)  (3 4)

这六种中

(2 3)  (2 4)  (3 4)可以拆分为：

(2 3)=(1 2)(1 3)(1 2)

(2 4)=(1 2)(1 4)(1 2)

(3 4)=(1 3)(1 4)(1 3)

所以，所有24种置换都可以由(1 2) (1 3) (1 4)三种互换生成。而生成关系可以画成一张图，称为凯莱图。这个非常重要，是凯莱图的理论基础。

首先考虑只有一种置换，那么凯来图很简单，只有两个元素

E 、(1 2)

只有两种的置换，凯来图是六个元素组成的环。

如下图

注意：上图的路径是(1 2)与(1 3)交替进行。

这个置换凯莱图是更高阶的置换凯莱图的基础，因为更高级的置换是无数个这样的六边形组成的。

四个元素的凯来图是，也是有多个六边形组成的。但是凯莱图很难画出。因为每个点连接三个六边形。总共24个点。

凯来图比较复杂，如下：

图中

黑色线条代表(1 2)

红色线条代表(1 3)

蓝色线条代表(1 4)

需要注意的是上图，有几个六边形特别难发现，这长得像核辐射符号。比如：

(1 3 4 2)->(2 3 4)->(1 4 2 3)->(1 4 2)->(2 4)->(1 2)(3 4)

那么总共有几个六边形呢？

我们可以这样计算，总共24个节点，每个六边形拥有6个节点。但是每个点属于三个六边形，也就是每个六边形实际上占有两个点。那么就是12个六边形。我们肉眼能直接看到7个六边形加上两个个辐射符号，再加上三个线轴形，也就是12个啊。

1个正六边形挨着六个不规则六边形

1个不规则六边形挨着1个正六边形，两个不规则六边形，1个核辐射，两个线轴

1个核辐射挨着3个不规则六边形，三个线轴

1个线轴挨着4个不规则六边形，两个核辐射

超过四元素的置换凯莱图特别复杂，所以用凯莱图计算置换会非常吃力，最好使用代数运算或者数值运算的方法进行计算。

不过对于大于四元素的置换凯来图也不必要那么慌，可以利用子群的方法去解开。比如从e出发的以(1 2) (1 3)交替前进的就是一个子群。

这个子群的表示方法为。(1 2)和 (1 3)是路径，也叫生成元。那么再看那三个线轴符号，也是红黑两种线组成，这个叫左陪集。左陪集的意思是由非子群内单位元开始，生成的集合。以横着的线轴为例子，用左陪集表示就是(1 2)(3 4)表示以(1 2)(3 4)出发，沿着路径(1 2)和(1 3)往前走，形成一个六边形。

所以这个复杂的置换群，可以拆分为一个子群和三个左陪集。

可以这样拆成四个：

(1 4)

(2 4)

(3 4)

置换的代数运算就是去掉表示位置，纯粹用符号运算。以下就是置换代数运算的例子：

(a b c)·(a d)·(a b c)2=(c d)

(a b c)2· (a d)·(a b c)=(b d)

这种运算，只需要把前面介绍的化简方法改成代数符号运算就可以了。

比如运算(a b c)·(a d)·(a b c)2

(a b c)·(a d)·(a b c)2

=(a b c d)  (a b c)2

利用乘方计算法则计算

(a b c)2=(a c b)

∴

(a b c d) ·(a b c)2

= (a b c d)* (a c b)

再用最原始办法，写出四个元素的位置映射

a->b->a

b->c->b

c->d

d->a->c

所以结果为(c d)

另一个我就不详细写出了。