简单易懂地向你解释:离散函数,差分,二阶差分和 Laplacian 滤波原理 |
您所在的位置:网站首页 › 数列的差分 › 简单易懂地向你解释:离散函数,差分,二阶差分和 Laplacian 滤波原理 |
简单易懂地向你解释:离散函数,差分,二阶差分和 Laplacian 滤波原理
|
离散函数
什么是离散函数?我们来看几个例子: 再看下图这是 f(x) = sin x + sin {x \ 2} 当 x 是 1\2 的整数倍时的图像。是离散的。这样 差分就是相邻两个离散值的差。以函数 f(x) = x^2, x ∈Z为例 xf(x)112439416525对于 x = 1,我们可以知道: f(1) = 1 \f(1 + 1) = 4 那么差分 Delta f(1) = f(1+1) - f(1) = 4 - 1 = 3 内容补充 这样用x+1和 x作差的差分,称为向前差分,记号是Delta。另有: f(x_i) - f(x_i - h):向后差分,记作 nabla f(x_i + h) - f(x_i - h) :中心差分。 如果进行一次泰勒展开,还能得到一阶微分的中心差商,可用于更高精度要求。有兴趣的可以自行了解。 x f(x) Delta f(x) 1 1 3 2 4 5 3 9 7 4 16 9 你会发现执行一次差分之后,差分值为等差数列。实际上运用这个特点可以让电路进行求导等数学操作,神奇吧? 我们对Delta f(x)也执行差分,也就是差分的差分,称为二阶差分。 x f(x) Delta f(x) Delta ^2f(x) 1 1 3 2 2 4 5 2 3 9 7 2 二阶差分之后,我们得到了常数列。可以发现差分的作用和求导是十分类似的。 偏导数的差分形式
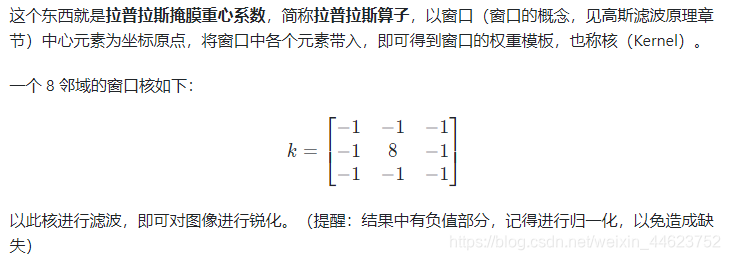
差分和导数类似,可以反映变化的快慢。对灰度不同的两个像素进行差分,得到的值就是两个像素的过渡急缓。而过度急剧的地方,往往就是图像中物体的边缘,因此我们认为:一阶差分可以检测边缘存在的可能性。这是一阶差分在这里的实际意义。 那么如果是二阶差分呢?在物理学中,对于位移 x ⃗ \vec{x} x 和时间 t t t,一阶导数表示速度,二阶差分表示速度的导数加速度。同样的,在图像处理上,一阶差分表示相邻像素的过渡急缓,二阶差分就表示这种过度急缓的变化强弱,可能你还是不明白,没关系,我们会在下面进一步解释。 如果一阶差分就能检测边缘,我们为什么还要二阶差分呢? 我们看下面的图: |
【本文地址】
今日新闻 |
推荐新闻 |
 这是 f(x) = sin x + sin {x \2}的函数图像。它的定义域是 R,是连续的。
这是 f(x) = sin x + sin {x \2}的函数图像。它的定义域是 R,是连续的。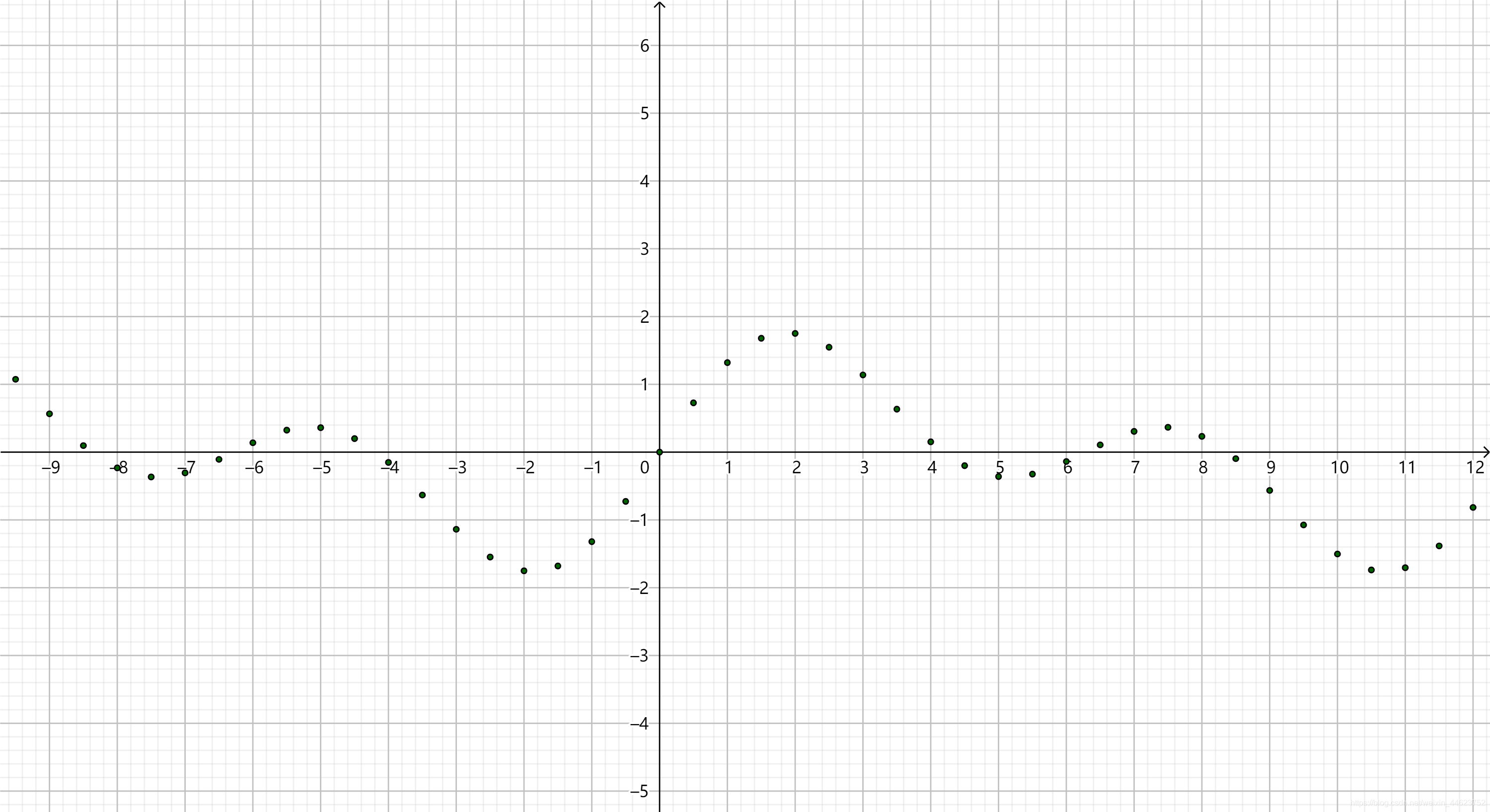 如果再苛刻一点,定义域是自然数集,值域是实数域,那么这样的函数就是离散数值函数
如果再苛刻一点,定义域是自然数集,值域是实数域,那么这样的函数就是离散数值函数
 这是一张从白到黑均匀渐变的图案,如果交给一阶差分来从上往下分析,会发现差分值一直都存在。于是一阶差分滤波器告诉你:这里全是边缘。但是这和我们的常识是不符的,因为虽然灰度变化了,但是变化的趋势却是均匀的。那么怎么样才能正确判断这是不是边缘呢?聪明的你应该想到了,用二阶差分来看,差分值一直是 0,说明变化是十分均匀的,说明边缘并不存在。因此,二阶差分才是真能确定边缘的存在性。
这是一张从白到黑均匀渐变的图案,如果交给一阶差分来从上往下分析,会发现差分值一直都存在。于是一阶差分滤波器告诉你:这里全是边缘。但是这和我们的常识是不符的,因为虽然灰度变化了,但是变化的趋势却是均匀的。那么怎么样才能正确判断这是不是边缘呢?聪明的你应该想到了,用二阶差分来看,差分值一直是 0,说明变化是十分均匀的,说明边缘并不存在。因此,二阶差分才是真能确定边缘的存在性。