収束する数列は有界であることの証明 |
您所在的位置:网站首页 › 数列有界 › 収束する数列は有界であることの証明 |
収束する数列は有界であることの証明
|
収束する数列は有界であることを証明します。数列の極限を厳密に定義する \varepsilon \text{-} N 論法の演習の一つとしても最適なので,しっかり確認しましょう。 定理の主張~収束⇒有界~収束・有界の定義の復習定理の証明逆は成り立たないが,収束部分列は存在する「収束の基本的なこと」に関する他の話題定理の主張~収束⇒有界~定理(収束する数列は有界) \{a_n\} を収束する数列とする。このとき,この数列は有界である。 証明する前に「収束する」の定義,「有界である」の定義を復習しておきます。 収束・有界の定義の復習定義(数列の収束) \{a_n\} を数列とする。 \{a_n\} が \alpha に収束する (converge) とは, 任意の \varepsilon > 0 に対して,ある N \ge 1 が存在して, n \ge N \implies |a_n - \alpha | < \varepsilonとなることである。 イプシロンエヌ論法ですね。これについては,以下の記事で長文にわたって詳しく解説しています。 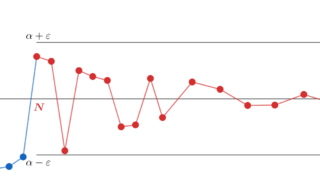 イプシロンエヌ論法をわかりやすく丁寧に~数列の極限の定義~数列の極限を厳密に定義するε-N論法について,その定義とイメージを具体例を交えて詳細に解説します。収束するものと,±∞に発散するものを分けて扱います。最後には,ε-N論法の否定も扱います。長文記事ですから,腰を据えて読み進めていきましょう。 イプシロンエヌ論法をわかりやすく丁寧に~数列の極限の定義~数列の極限を厳密に定義するε-N論法について,その定義とイメージを具体例を交えて詳細に解説します。収束するものと,±∞に発散するものを分けて扱います。最後には,ε-N論法の否定も扱います。長文記事ですから,腰を据えて読み進めていきましょう。定義(数列の有界性) \{a_n\} を数列とする。 \{a_n\} が有界である (bounded) とは, ある K > 0 が存在して, |a_n| \le K, \quad (n \ge 1 )となることである。 各 n \ge 1 によらずに,大きさが定数 K で抑えられるということですね。これについては,以下でも解説しています。 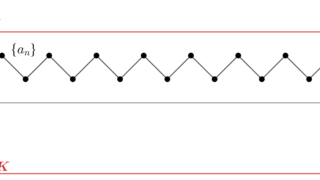 有界とは何か~有界数列(点列)・有界関数・有界集合(区間)~数学における有界 (bounded) とは,簡単に言うと無限遠に飛んでいかないということです。特に,有界数列(点列)・有界関数・有界集合(区間)の3つについて,その定義を,イメージ図を添えて解説します。最後には,有界に関する話題も列挙します。 有界とは何か~有界数列(点列)・有界関数・有界集合(区間)~数学における有界 (bounded) とは,簡単に言うと無限遠に飛んでいかないということです。特に,有界数列(点列)・有界関数・有界集合(区間)の3つについて,その定義を,イメージ図を添えて解説します。最後には,有界に関する話題も列挙します。さて,定理を証明していきましょう。 証明 \lim_{n\to\infty} a_n = \alpha とする。 \varepsilon > 0 を一つ定めると,収束の定義から,ある N \ge 1 が存在して, n \ge N \implies |a_n - \alpha | < \varepsilonとなる。ここで, K = \max\{|a_1|, |a_2|,\ldots, |a_{N-1}|, |\alpha| + \varepsilon\}と定めると, |a_n| \le K, \quad (n \ge 1 )であり,有界である。 証明終 証明は短いかもしれません。図で表現すると,以下のような理屈です。 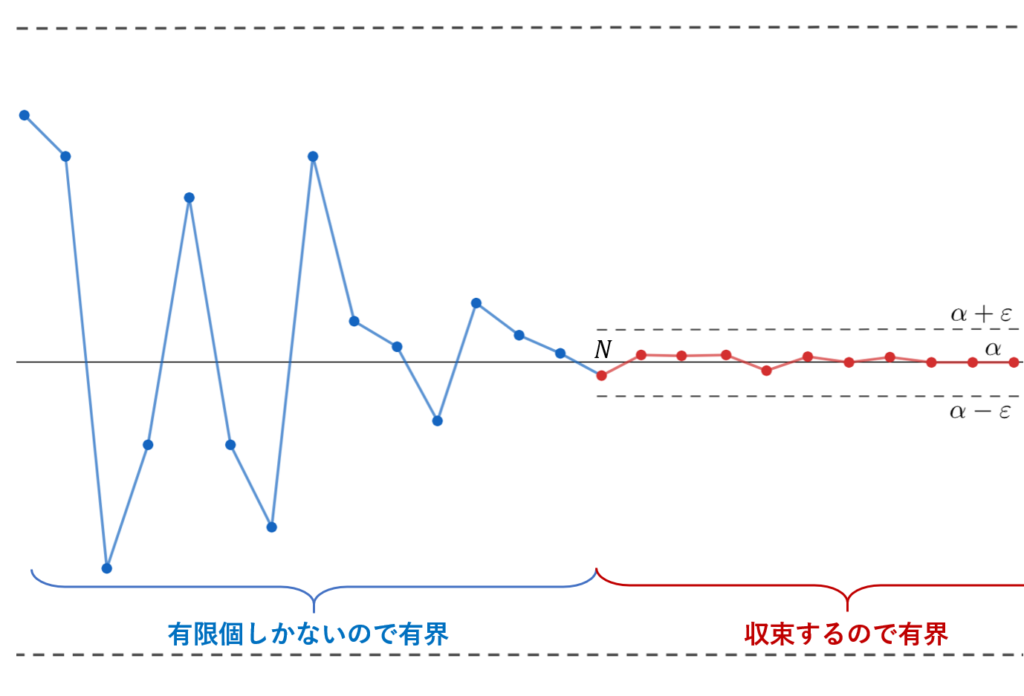 この定理は周知の事実ですから,しっかりと覚えておきましょう。 逆は成り立たないが,収束部分列は存在するここまで,「収束 \implies 有界」を証明しましたが, 一般に逆,すなわち「有界 \implies 収束」は成立しません。 ですが,部分列であれば, 収束するものが存在することが知られています。これを,ボルツァノ-ワイエルシュトラスの定理 (Bolzano- Weierstrass Theorem) と言います。これの証明は,以下の記事で解説しています。 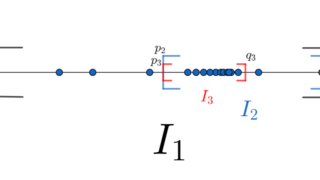 ボルツァノ–ワイエルシュトラスの定理とその証明大学教養数学のさまざまなところに登場する,ボルツァノ–ワイエルシュトラスの定理 (Bolzano–Weierstrass Theorem) について紹介します。まず1次元の場合を紹介し,次に多次元の場合を紹介して,最後に位相空間論の言葉を用いて述べます。 ボルツァノ–ワイエルシュトラスの定理とその証明大学教養数学のさまざまなところに登場する,ボルツァノ–ワイエルシュトラスの定理 (Bolzano–Weierstrass Theorem) について紹介します。まず1次元の場合を紹介し,次に多次元の場合を紹介して,最後に位相空間論の言葉を用いて述べます。 |
【本文地址】
今日新闻 |
推荐新闻 |