数值分析上机题Matlab

您所在的位置：网站首页 › 数值计算方法第四章答案 › 数值分析上机题Matlab

数值分析上机题Matlab

#数值分析上机题Matlab| 来源: 网络整理| 查看: 265

第二章上机题 Newton迭代法

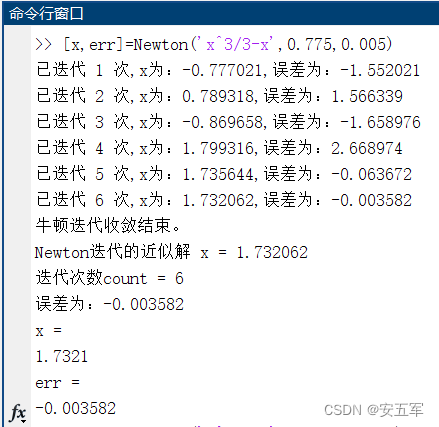
function [x,err]=Newton(f,x0,epsilon) %用例：[x,err]=Newton('x^3/3-x',0.7,0.005) %Input - f 字符串公式'x^3/3-x' % - x0 迭代初值 % - epsilon 是迭代精度要求 %Output – x 是最后迭代的近似结果 % - err 是最后得到的误差 syms x f=str2sym(f); f(x)=f; df(x)=diff(f(x)); phi(x)=x-f(x)/df(x); restrain=1; count = 0; e = 1; while abs(e)>epsilon x1=phi(x0); e=x1-x0; x0=x1; count = count+1; fprintf('已迭代%d次,', count) fprintf('x位：%f,', x0) fprintf('误差为：%f\n', e) if count>100 fprintf('牛顿迭代发散\n') restrain=0; break end end if restrain==1 fprintf('牛顿迭代收敛结束\n') fprintf('Newton迭代的近似解 x = %f\n',x0) fprintf('迭代次数count = %d\n',count) fprintf('误差为：%f\n', e) end err=vpa(e); x=vpa(x0); end

解：利用二分法在[0.7,0.8]中寻找δ，最终保留四位有效数字，得到δ=0.7625，运行结果如图1所示：

图1 二分法求解结果

②试取若干初始值，观察当x0∈-∞,-1，-1,-δ，-δ,δ，δ,1 ，1,+∞ 时Newton序列是否收敛以及收敛于哪一个根。

当x0∈-∞,-1时，Newton序列收敛，收敛于x1*=-3；

当x0∈-1,-δ时，Newton序列收敛，收敛于x1*=-3或者x3*=3；当x0取-0.81时收敛于3，而当x0取-0.8时收敛于-3；

当x0∈-δ,δ时，Newton序列收敛，收敛于x2*=0；

当x0∈δ,1时，Newton序列收敛，收敛于x1*=-3或者x3*=3；当x0取0.81时收敛于-3，而当x0取0.8时收敛于3；

当x0∈1,+∞时，Newton序列收敛，收敛于x3*=3；

在第二题中通过取不同的初值，即使相邻很近，但会收敛到不同的相距较远的根，我将函数曲线可视化出来，如图2所示，我的想法是，在-1的领域中，曲线斜率变化很小，会使得迭代方程的结果跳跃到别处，但由于这个函数整体是收敛的，故迭代值的跳跃并没有影响其可以得到一个结果，但这种函数我认为是不稳定的，如果在工程实践中，有这样的一个问题，输入初值是测量值，但由于各种外界因素的影响使其受到很小扰动时，得到的结果是不同的，这样是不希望发生的。所以我认为，应该尽量将方程的根求出来，当可行性较差时，也应该分析系统的灵敏性。

图2 x^3/3-x函数图像

第三章上机题逐次超松弛迭代法

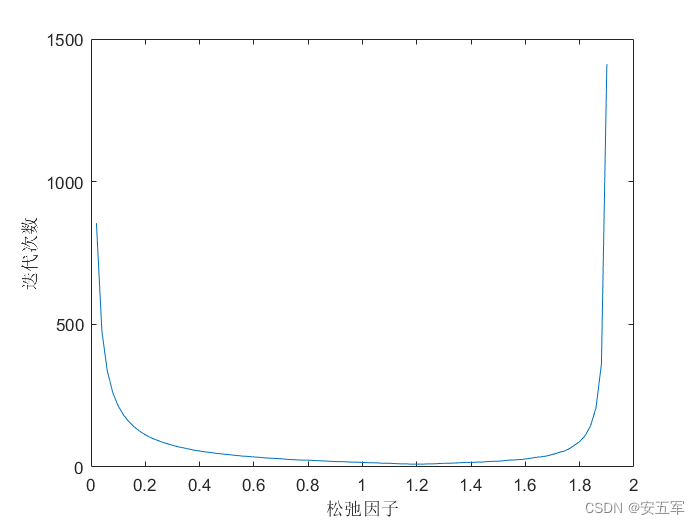
function [x,e,count] = SOR(A,b,x,omg) %SOR 用例 %A=[31,-13,0,0,0,-10,0,0,0;-13,35,-9,0,-11,0,0,0,0;0,-9,31,-10,0,0,0,0,0;0,0,-10,79,-30,0,0,0,-9;0,0,0,-30,57,-7,0,-5,0;0,0,0,0,-7,47,-30,0,0;0,0,0,0,0,-30,41,0,0;0,0,0,0,-5,0,0,27,-2;0,0,0,-9,0,0,0,-2,29]; % b=[-15,27,-23,0,-20,12,-7,7,10]'; % x=[0,0,0,0,0,0,0,0,0]'; % omg=0.02; % [x,e,count] = SOR(A,b,x,omg) %Input - A 系数矩阵 % - b 结果向量 % - x 初始迭代向量 % - omg松弛因子 %Output - x 是迭代结果 % - e 最后最大误差 % - count 迭代次数 n=length(x); z=x; X=[x]; e=1; count=0; while e>0.000005 for i=1:n summ=0; for j=1:n if i~=j summ=summ+A(i,j)*z(j); end end z(i)=(1-omg)*z(i)+omg*( b(i)-summ )/A(i,i); end X=[X,z]; e=max(abs(z-x)); x=z; count=count+1; if e>1000 count=NaN; fprintf('超松弛因子为：%f，迭代发散\n', omg) break end end if flag==1 fprintf('超松弛因子为：%f，迭代收敛，', omg) fprintf('迭代次数为：%d。 ', count) end end

运用第一问中编好的通用程序再次编程，解答程序如下：

clear,clc Count=[]; X=[]; E=[]; A=[31,-13,0,0,0,-10,0,0,0;-13,35,-9,0,-11,0,0,0,0;0,-9,31,-10,0,0,0,0,0;0,0,-10,79,-30,0,0,0,-9;0,0,0,-30,57,-7,0,-5,0;0,0,0,0,-7,47,-30,0,0;0,0,0,0,0,-30,41,0,0;0,0,0,0,-5,0,0,27,-2;0,0,0,-9,0,0,0,-2,29]; b=[-15,27,-23,0,-20,12,-7,7,10]'; for i=1:99 x=[0,0,0,0,0,0,0,0,0]'; omg=i/50; [x,e,count] = SOR(A,b,x,omg); X=[X,x]; E=[E,e]; Count=[Count,count]; end Omg=0.02:0.02:1.98; plot(Omg,Count) BestC=find(Count==min(Count)); fprintf('最佳松弛因子为\n') BestOmg=Omg(BestC)

取0向量为初始迭代向量，运行结果如图3所示：

图3 SOR收敛过程

将结果汇总如下表：

松弛因子

迭代次数

松弛因子

迭代次数

松弛因子

迭代次数

松弛因子

迭代次数

0.02

855

0.52

1.02

1.52

0.04

477

0.54

1.04

1.54

0.06

336

0.56

1.06

1.56

0.08

261

0.58

1.08

1.58

0.10

214

0.60

1.10

1.60

0.12

182

0.62

1.12

1.62

0.14

158

0.64

1.14

1.64

0.16

140

0.66

1.16

1.66

0.18

125

0.68

1.18

1.68

0.20

113

0.70

1.20

1.70

0.22

103

0.72

1.22

1.72

0.24

0.74

1.24

1.74

0.26

0.76

1.26

1.76

0.28

0.78

1.28

1.78

0.30

0.80

1.30

1.80

0.32

0.82

1.32

1.82

110

0.34

0.84

1.34

1.84

144

0.36

0.86

1.36

1.86

207

0.38

0.88

1.38

1.88

361

0.40

0.90

1.40

1.90

1412

0.42

0.92

1.42

1.92

发散

0.44

0.94

1.44

1.94

发散

0.46

0.96

1.46

1.96

发散

0.48

0.98

1.48

1.98

发散

0.50

1.00

1.50

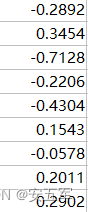
图4 松弛因子与迭代次数关系

如表格和图4所示，最佳松弛因子为1.18、1.20、1.22，迭代次数为10，解向量为：

可以看出，比ω=1时的Gauss-Seidel迭代法迭代次数16次要更优，但当ω取值较小或大时会迭代上千次，甚至发散。

第四章上机题 3次样条插值函数

function yy=cubic_spline(x,y,xx) % 用例 % x=[0,1,2,3,4,5,6,7,8,9,10]; %y=[2.51,3.30,4.04,4.70,5.22,5.54,5.78,5.40,5.57,5.70,5.80]; % xx=[0.5:1:9.5]; % yy=cubic_spline(x,y,xx) %Input - x 已知数据的x坐标 % - y 已知数据的y坐标 % - xx 预测位置数据 %Output - yy 三次样条插值输出结果 %第一型，已知两端点处f(x)的1阶导数 f1(1)=0.8; f1(2)=0.2; n=length(x); h=[]; for i=1:n-1 h(i)=x(i+1)-x(i); end f=[]; for i=1:n-1 f(i)=(y(i+1)-y(i))/h(i); end miu=[]; for i=1:n-2 miu(i)=h(i)/(h(i)+h(i+1)); end d=[]; for i=0:n-1 if i==0 d(i+1)=(f(i+1)-f1(1))/(h(i+1)); elseif i==n-1 d(i+1)=(f1(2)-f(i))/(h(i)); else d(i+1)=(f(i+1)-f(i))/(h(i)+h(i+1)); end end A=[]; for i=1:n A(i,i)=2; if i==1 A(i,i+1)=1; elseif i==n A(i,i-1)=1; else A(i,i+1)=1-miu(i-1); A(i,i-1)=miu(i-1); end end B=6.*d'; M=A\B; %求解M向量 %构造最后的插值分段函数 s2=[]; for i=1:n-1 s2(i)=f(i)-(1/3*M(i)+1/6*M(i+1))*h(i); end s3=[]; for i=1:n-1 s3(i)=1/2*M(i); end s4=[]; for i=1:n-1 s4(i)=1/6/h(i)*(M(i+1)-M(i)); end S=[y(1:n-1)',s2',s3',s4']; a=x; digits(5) for i=1:n-1 syms x l1(x) = S(i,2) * (x - a(i)); l2(x) = S(i,3) * (x - a(i)) ^ 2; l3(x) = S(i,4) * (x - a(i)) ^ 3; fprintf("-------------------------------------\n") Sx(x) = S(i,1) + l1 + l2 +l3; Sx(x) = vpa(Sx); fprintf('S(x)=%s \t x∈(%d,%d)\n',char(Sx),i-1,i); end fprintf("\n\n\n") yy=[]; for i=1:length(xx) sec=xx(i)-a; for j=1:length(sec) if sec(j)0.00000000001 v(:,i)=A*v(:,i-1); m(i-1)=max(v(:,i)); v(:,i)=v(:,i)/m(i-1); n=max(v(:,i)-v(:,i-1)); i=i+1; end fprintf('幂法计算的最大特征值为：%s \n',m(i-2)); fprintf('使用eig计算得到的最大特征值为：%s \n',max(eig(A))); fprintf('最大特征值对应的特征向量为：º\n'); v(:,i-1)*m(i-2)

计算结果如图8所示：

图8 矩阵特征值计算结果

由结果可知，使用幂法计算得到的矩阵最大特征值与使用eig函数计算得到的最大特征值结果一致，证明了幂法程序的正确性。

【本文地址】

数值分析上机题Matlab

数值分析上机题Matlab

今日新闻

推荐新闻