Runge 现象的数学解释 |
您所在的位置:网站首页 › 插值余项定理证明 › Runge 现象的数学解释 |
Runge 现象的数学解释
|
目录 Runge 现象考虑如下的 Runge 函数\[ f(x)= \frac{1}{1+25x^2}.\]Runge 发现如果利用区间 [-1,1] 上的等距节点\[ x_i= -1 + \frac{2i}{n},\quad i=0,1,2,…,n\]构造插值多项式 \(P_n(x)\), 那么它会在趋于区间端点时出现大幅震荡. 理论上可以证明插值误差会随多项式阶数的增加趋于无穷大:\[ \lim_{n\to\infty} \left( \max_{-1\leq x\leq 1}|f(x)-P_n(x)| \right)=\infty.\]这说明了, 采用等距节点构造高阶插值多项式的做法有时并不可取. 下面的动图生动地展示了所谓的 Runge 现象 – 插值多项式在区间的两个端点附近会产生震荡现象, 并且多项式次数越高振荡越明显. (Python 代码实现见附录) 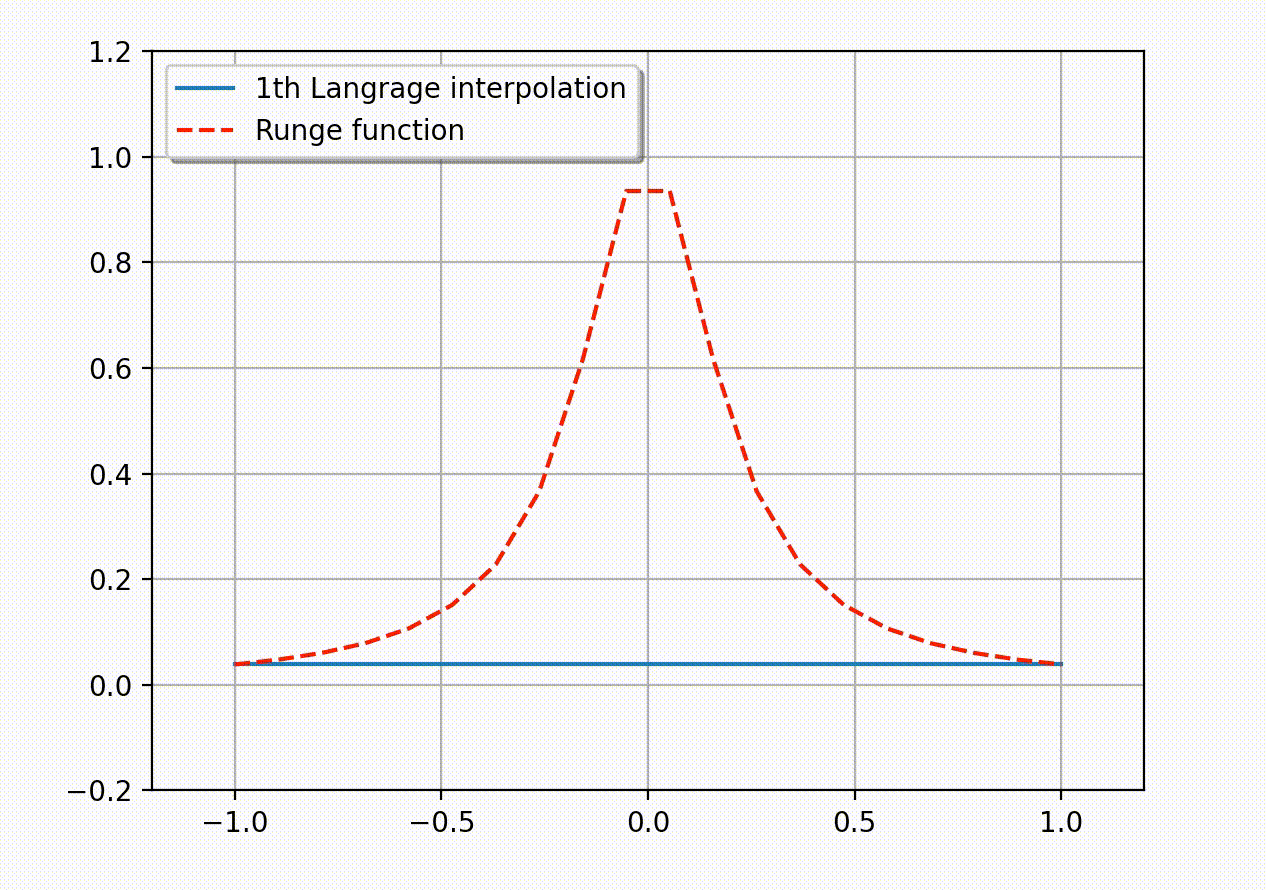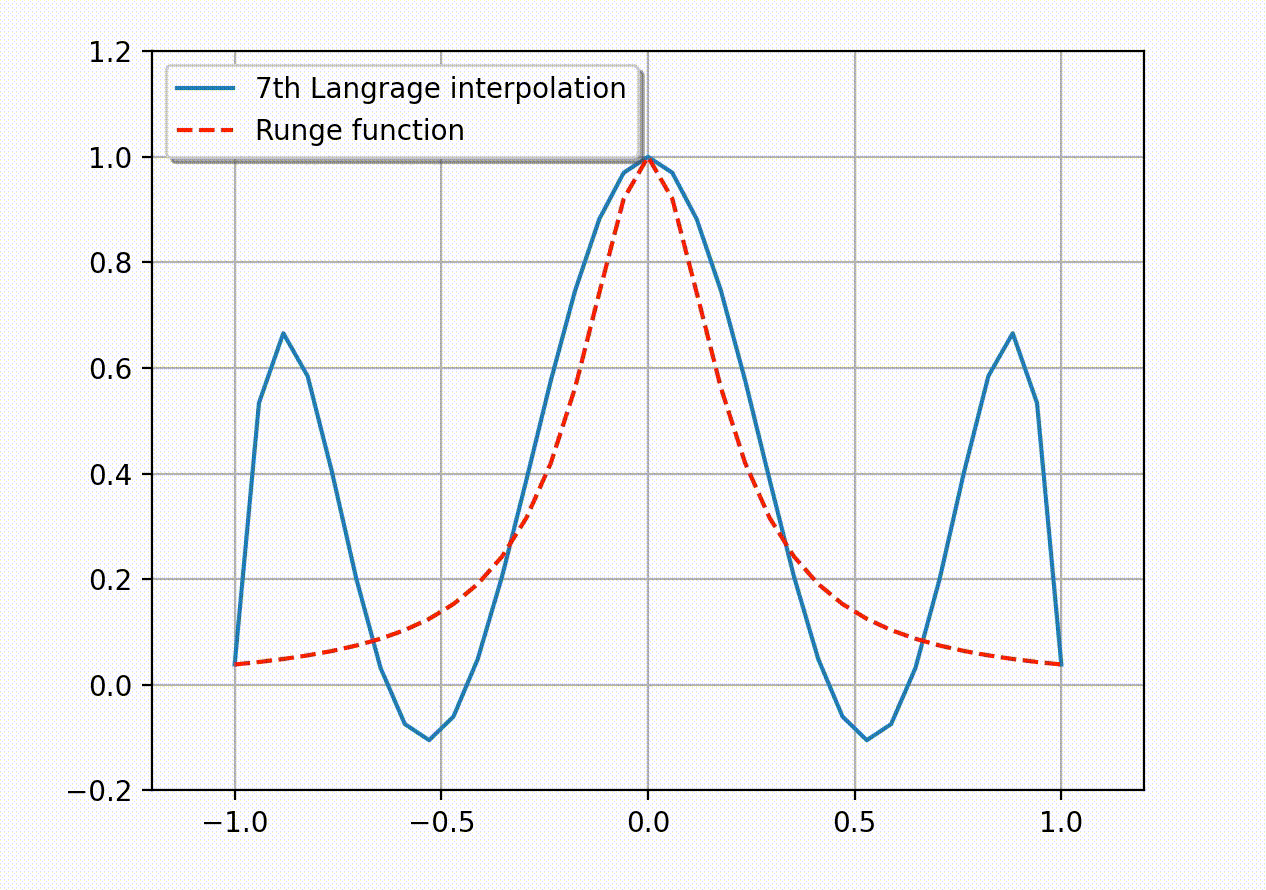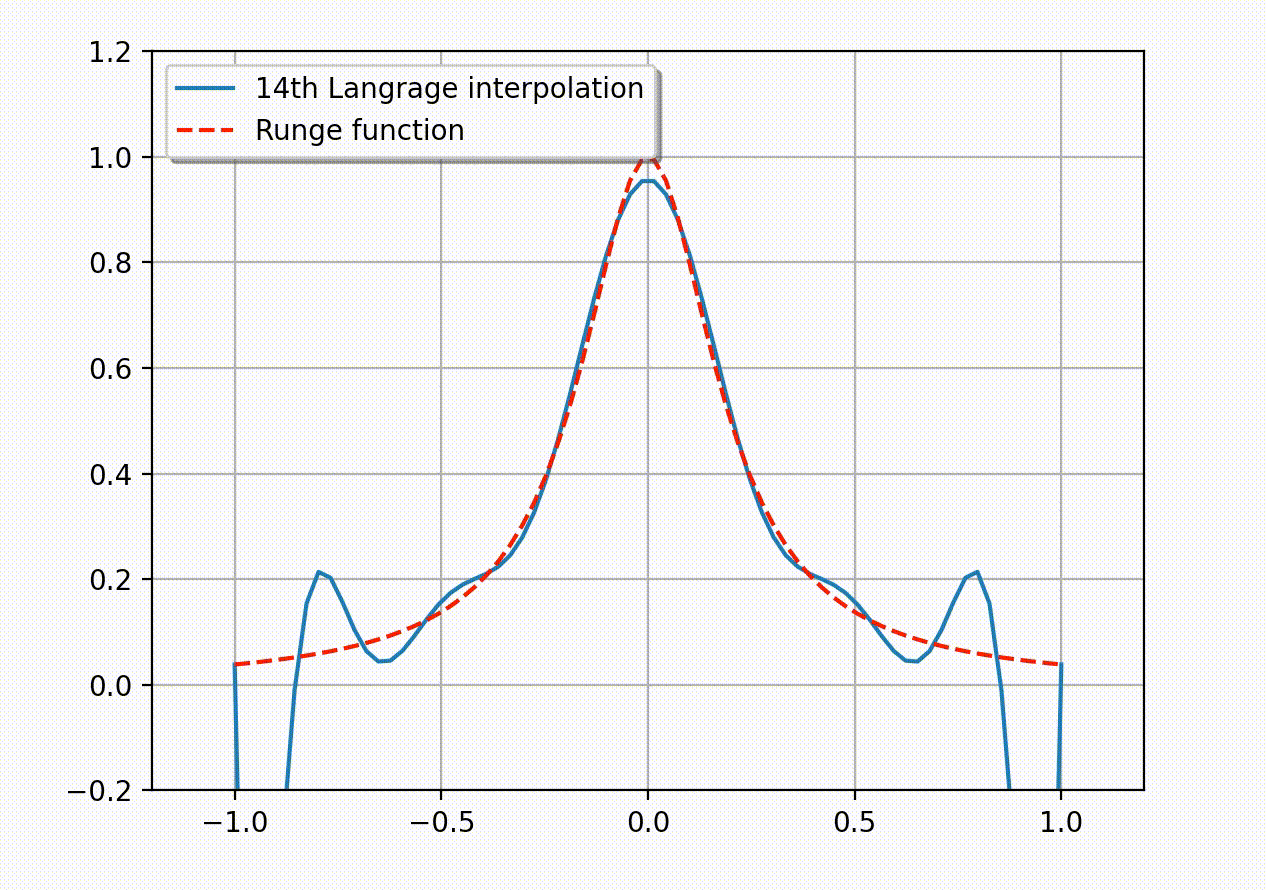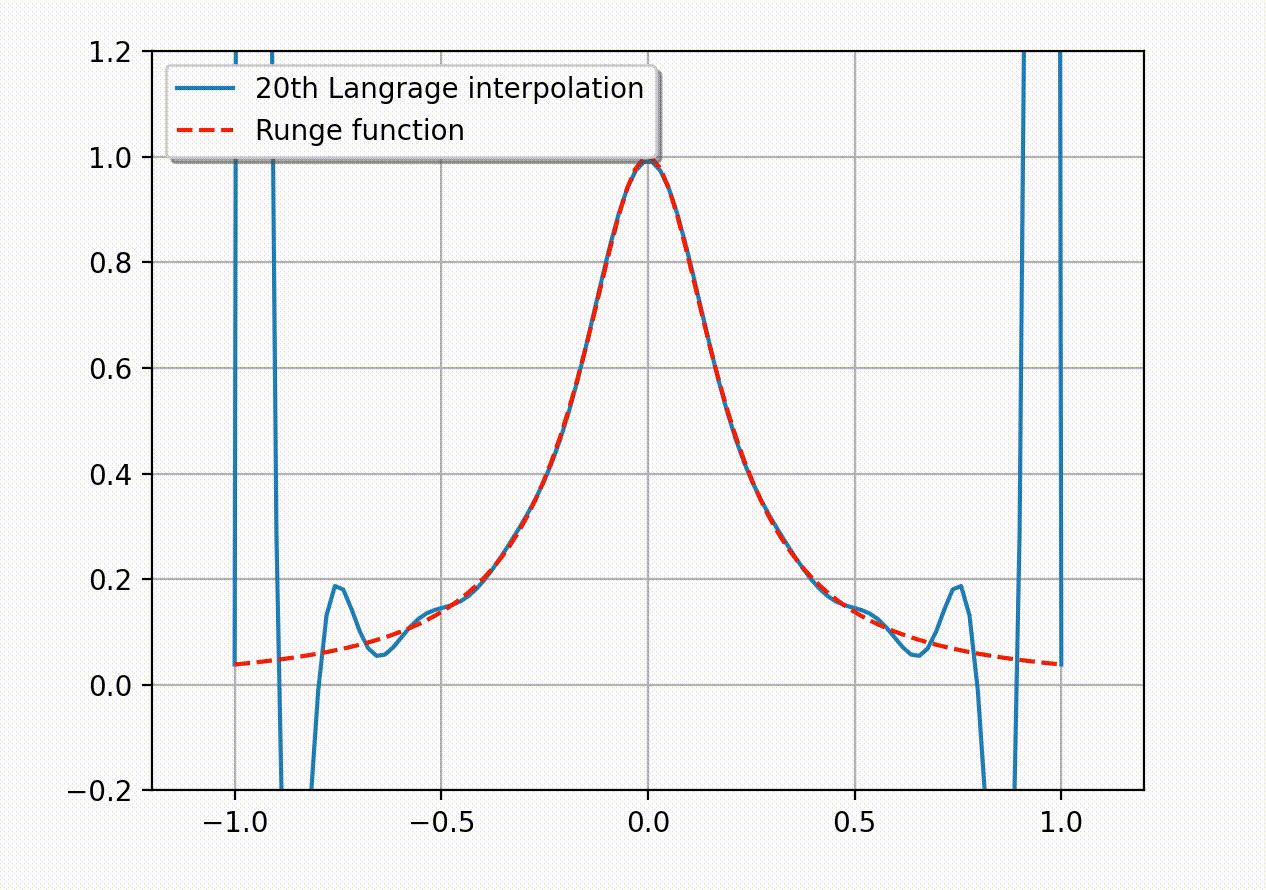 Runge 现象 Runge 现象
在下面的章节中, 我们将从理论上提示上述发散现象产生的原因. 在此之前, 我们有必要说明一下证明需要的数学基础: 关于极限的定义和基本内容复变函数论中的单极点, 留数和留数定理牛顿插值 (利用差商构造的插值多项式)Chebyshev 多项式 余项理论定理 1 (余项估计) 令 \(f(x)\in C^n[a,b]\) 并假设 \(f^{n+1}(x)\) 在区间 \((a,b)\) 上是有定义的.\[ R_n(x):=f(x)-p_n(x) = \frac{1}{(n+1)!}\prod_{i=0}^n (x-x_i) f^{n+1}(\xi) \tag{1}\]其中, \(a |
【本文地址】
今日新闻 |
推荐新闻 |