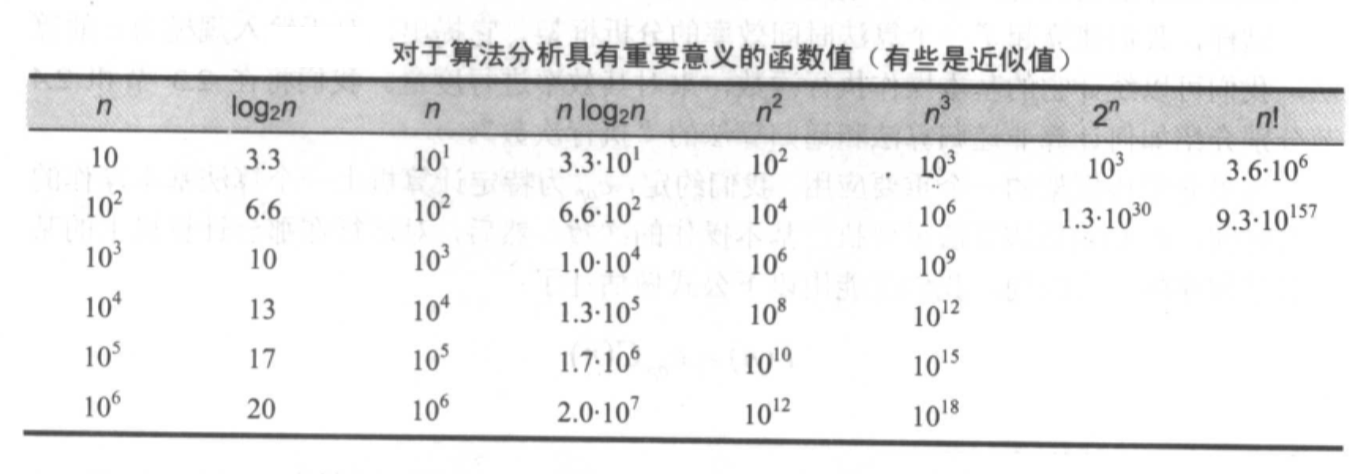
除了正确性，算法的另外一个重要的特就是效率(Efficiency)了。有两种算法效率：时间效率(Time Efficiency)和空间效率(Space Effiency)。时间效率也称为时间复杂度(Time Complexity)，指出算法运行有多快；空间效率有称为空间复杂度(Space Complexity)，指出算法需要多少额外的空间。 在电子计算机时代早期（大规模集成电路出现前），时间和空间是两种极其昂贵的资源。但经过半个多世纪的技术革新，计算机的执行速度和存储容量已经提升了好几个量级。现在，一个算法所需的额外空间已经不是重点关注的问题。然而，时间效率的重要性并没有减弱到这种程度。随着问题规模的扩大，时间效率则变得更加突出。需要说明的是，不重点关注空间并不代表不需要关注空间。如在编码中，如果可以使用integer类型存储数据，则没有必要使用long。可以使用set存储元素，则没有必要使用map，等等。由于对时间的关注度基本决定了算法的选择，所以本文将仅分析时间效率。注意，这里介绍的分析方法也适用于空间效率。 一般来说，一个问题通常有多个候选算法。通过算法效率分析，我们可以抛弃低效率的算法，选出一个合适现有场景的算法。

对于算法，需要考虑相同问题，更大规模的处理效率。一般情况下，将规模 n n n作为算法的输入参数。在大多数情况下，选择何种参数是非常直接的。如，对于排序、查找、寻找列表的最小元素等问题来说，这个参数就是列表的长度。 注意，有些情况下，选择哪个参数表示输入规模是由差别的。如，计算两个 n n n阶矩阵的乘积。对这个问题来说，有两种度量的方法。第一种方法，是用矩阵的阶 n n n。另一种方法是，参加乘法运算的矩阵中所有元素的个数 N N N。 如何恰当的选择输入规模的度量单位，还要受到所讨论算法的操作细节影响。如对于一个拼写检查算法，如果需要对于每个字符进行检查，则应使用字符的数量作为输入规模；如果需要对每个单位进行检查，则应使用单词的数量作为输入规模。

明确问题的输入规模后，接下来考虑算法运行时间的度量。我们的第一直觉是使用是时间来度量算法的运行时间。然而，这种方法有一些明显的缺陷：它依赖于特定计算机的运行速度，依赖于算法实现的质量，等等。因为我们寻求的是算法效率的度量标准，所以应选择一个不依赖于上述无关因素的度量标准。 然后，我们尝试考虑统计算法每一步操作的执行次数。从数学的角度来说，统计所有操作的执行次数没有必要。因为随着输入规模的不断变大，算法效率主要受执行量级最大的操作影响。举例来说，如果一个算法所有操作的执行次数是 a n x n + . . . + a 1 x 1 + a 0 a_nx^n +... +a_1x^1 + a_0 an​xn+...+a1​x1+a0​，随着n的次数不断增大，其近似值为 x n x^n xn。所以，我们应该找出算法中最重要的操作，即所谓的基本操作(basic operation)，它们对总运行时间的贡献最大，然后计算它们的运行次数。 这样，我们就可建立一个算法时间效率的分析框架：对输入规模为n的算法，可以通过统计它的基本操作执行次数，来对其效率进行度量。该算法时间效率分析框架的应用如下： 如果我们需要计算运行在某台计算机上的某个算法的运行时间，我们可以使用如下公式： T ( n ) = c o p C ( n ) T(n) = c_{op}C(n) T(n)=cop​C(n) 其中， c o p c_{op} cop​表示指定计算机该算法上一个基本操作的执行时间， C ( n ) C(n) C(n)则是该算法需要执行基本操作的次数。

对于大规模的输入，算法效率分析框架，会忽略乘法常量，而仅关注执行次数的增长次数(order of growth)及其常数倍。为什么要对大规模的输入强调执行次数的增长次数呢？这是因为小规模输入在运行时间上的差异不足以区分高效算法和低效算法。如计算两个数的gcd(最大公约数)，如果两个数较小，多个算法之间的效率差异并不是很明显。只有当两个数较大时，算法效率的差异才变得明显。下图列举了常见的函数增长次数：

由上图可知，对数函数的增长次数要小于 f ( n ) = n f(n)=n f(n)=n函数增长次数。另外，虽然特定的操作依赖对数的底，但因方程： l o g a n = l o g a b ∗ l o g b n log_a n = log_a b * log_b n loga​n=loga​b∗logb​n 允许对数在不同的底数进行转换，仅是新增一个乘法常量。所以，我们可以忽略对数的底，简写成 l o g n log n logn。 另外需要说明的就是幂函数 2 n 2^n 2n和阶乘函数 n ! n! n!。这两种函数增长次数太大，以至于即使n的值相当小，函数的值也会成为天文数字。当n等于100时，对一台每秒执行1万亿次( 1 0 12 10^{12} 1012)操作的计算机来说，大约需要 4 ∗ 1 0 10 4*10^{10} 4∗1010年才能完成计算。即使使用多核、多计算机，其时间消耗也是难以接受的。另外，虽然幂函数 2 n 2^n 2n和阶乘函数 n ! n! n!的增长次数不同，但是，由于两个函数的增长次数已经无法容忍，所以常常将两者都作为"指数级增长的函数"。我们仅推荐在已知且很小的规模下使用这两种函数级别的算法。

以算法输入规模作为参数的函数可以合理地度量算法的效率。但还有许多算法的运行时间不仅取决于输入的规模，还取决于特定输入的细节。接下来，将以顺序查找为例，简单说下输入细节对算法运行时间的影响。 假设有n个元素，存储在长度为n的列表中，其中每个元素有唯一KEY。为了找到特定的元素，需要检查列表中的每个元素，直到发现KEY匹配的元素为止或者到达列表的末尾，没有找到匹配的元素。该算法的伪代码实现如下：