描述性统计、参数估计和假设检验 |
您所在的位置:网站首页 › 描述统计推断统计简单区分 › 描述性统计、参数估计和假设检验 |
描述性统计、参数估计和假设检验
|
描述性统计分析
描述性统计所提取的统计的信息称为统计量,包括频数与频率,反映集中趋势的均值、中位数、众数和分位数,反映离散程度的极差、方差和标准差,反映分布形状(相对于正态分布)的偏度和峰度。 变量分为类别变量和数值变量,类别变量往往被作为维度,数值变量往往被作为指标。类别可以经过特定的转换转换为数值,从而作为指标,数值变量也可以经过特定的分箱或转换转换为文本型变量,从而作为类别或维度。 频数与频率最基本的统计量就是频数与频率,它们适用于类别变量。 频数,指数据中类别变量每个不同取值出现的次数。 频率,指每个类别变量的频数与总次数的比值,通常采用百分数表示。 下面我们以鸢尾花数据集为例说明这些概念,首先导包并读取数据: import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from sklearn.datasets import load_iris # 设置seaborn绘图的样式,并显示中文 sns.set(style="darkgrid") plt.rcParams["font.family"] = "SimHei" plt.rcParams["axes.unicode_minus"] = False iris = load_iris() data = np.column_stack([iris.data, iris.target]) data = pd.DataFrame(data, columns=["sepal_length", "sepal_width", "petal_length", "petal_width", "type"]) data.sample(10)
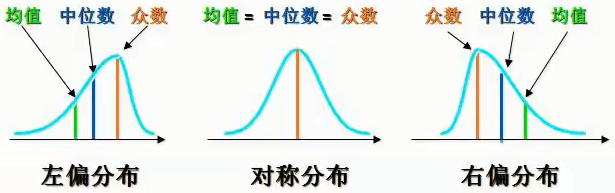
注意:column_stack会先将一维数组转换为2维列向量后,按列水平进行拼接 numpy拼接小知识补充 np.column_stack([iris.data, iris.target])等价于: np.hstack([iris.data, iris.target.reshape(-1, 1)])或: np.concatenate([iris.data, iris.target.reshape(-1, 1)], axis=1)或: np.c_[iris.data, iris.target.reshape(-1, 1)]而iris.target.reshape(-1, 1)也可以用新增轴来表示,等价于: iris.target[:, np.newaxis]np.newaxis的本质等于None,可以直接用None替换,即: iris.target[:, None]个人觉得column_stack最方便,因为实现了将一维数组自动转换为2维列向量。 下面计算鸢尾花数据中,每个类别出现的频数: frequency = data["type"].value_counts() frequency 2.0 50 1.0 50 0.0 50 Name: type, dtype: int64将频数除以总数即表示每个类别出现的频率,使用百分比表示: percentage = frequency * 100 / len(data) percentage 2.0 33.333333 1.0 33.333333 0.0 33.333333 Name: type, dtype: float64 反映趋中趋势的几个指标有均值、中位数、众数和分位数。 均值、中位数和众数均值,即平均值,其为—组数据的总和除以数据的个数。 中位数,将一组数据升序排列,位于该组数据最中间位置的值,就是中位数。如果数据个数为偶数,则取中间两个数值的均值。 众数,一组数据中出现次数最多的值
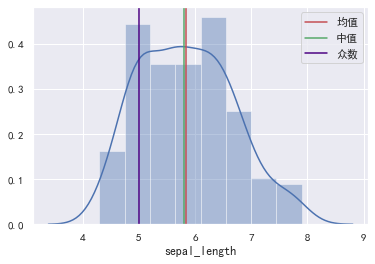
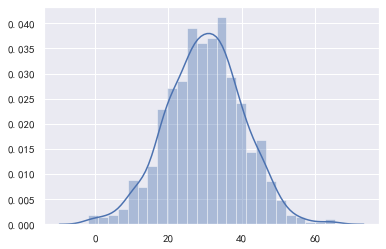
从上图可以看到在正态分布下,三者是相同的,在偏态分布下,三者会有所不同。 数值变量在正态分布时,可以使用均值与中值表示集中趋势。在偏态分布下,均值容易受极端值的影响,所以一般使用中值表示集中趋势。 类别变量通常使用众数表示集中趋势,但众数在一组数据中可能不是唯一的。 举个例子,要统计居民的总体收入水平,使用哪项指标衡量更合适呢?首先收入属于数值变量,可以使用均值与中位数表示集中趋势。 但20%的人掌握着80%的人财富,居民收入是个严重右偏的分布,均值会受极端值的影响,所以使用中位数指标更合适。 下面我们计算花萼长度的均值,中位数以及众数: # 计算花萼长度的均值。 mean = data["sepal_length"].mean() # 计算花萼长度的中位数。 median = data["sepal_length"].median() # 计算花萼长度的众数。 mode = data["sepal_length"].mode() print(mean, median) # mode方法返回的是Series类型。 print(mode) 5.843333333333335 5.8 0 5.0 dtype: float64也可以使用scipy的stats模块来求一组数据的众数。 from scipy import stats stats.mode(data["sepal_length"]) ModeResult(mode=array([5.]), count=array([10]))同时会返回该众数出现的频次。 看看分布: # 绘制数据的分布(直方图 + 密度图)。 sns.distplot(data["sepal_length"]) # 绘制垂直线。 plt.axvline(mean, ls="-", color="r", label="均值") plt.axvline(median, ls="-", color="g", label="中值") plt.axvline(mode, ls="-", color="indigo", label="众数") plt.legend()
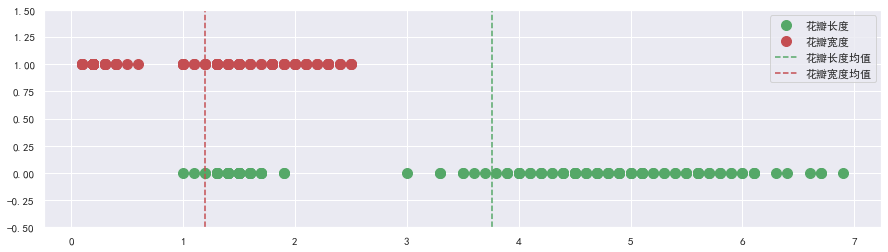
Serise的mode方法和stats.mode()方法的区别 Serise的mode方法的返回值类型是Serise。stats.mode()方法的返回值类型是 ModeResult 如果众数的值不唯一,Series的mode()方法会显示所有众数,而stats.mode()方法只显示其中一个,但同时能知道该众数的个数。 s = pd.Series([1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 5])对于Series的mode方法: s.mode() 0 1 1 2 2 3 dtype: int64对于stats.mode()方法: stats.mode(s) ModeResult(mode=array([1], dtype=int64), count=array([3])) 分位数分位数,通过n-1个分位将数据划分为n个区间,使得每个区间的数值个数相等(或近似相等)。其中,n为分位数的数量.常用的分位数有四分位数与百分位数。 以四分位数为例,通过3个分位,将数据划分为4个区间(百分位数可根据四分位数对比理解)。 第1个分位称为1/4分位(下四分位)数据中1/4的数据小于该分位值。第2个分位称为2/4分位(中四分位)数据中2/4的数据小于该分位值。第3个分位称为3/4分位(上四分位)数据中3/4的数据小于该分位值。使用Numpy中计算分位数: x = [1, 3, 10, 15, 18, 20, 23, 40] # quantile与percentile都可以计算分位数,不同的是,quantile方法, # q(要计算的分位数)的取值范围为[0, 1],而percentile方法,q的取值范围为[0, 100]。 print(np.quantile(x, q=[0.25, 0.5, 0.75])) print(np.percentile(x, q=[25, 50, 75])) [ 8.25 16.5 20.75] [ 8.25 16.5 20.75]使用Pandas中计算分位数: x = [1, 3, 10, 15, 18, 20, 23, 40] s = pd.Series(x) s.describe() count 8.000000 mean 16.250000 std 12.395276 min 1.000000 25% 8.250000 50% 16.500000 75% 20.750000 max 40.000000 dtype: float64describe方法支持自定义分位位置: s.describe(percentiles=[0.25, 0.9]) count 9.000000 mean 16.777778 std 11.702326 min 1.000000 25% 10.000000 50% 18.000000 90% 26.400000 max 40.000000 dtype: float64分位数计算的原理 首先计算分位点所在的索引位置: x = np.array([1, 3, 10, 15, 18, 20, 23, 40]) n = len(x) # 计算四分位的索引(index)。 q1_index = (n - 1) * 0.25 q2_index = (n - 1) * 0.5 q3_index = (n - 1) * 0.75 print(q1_index, q2_index, q3_index) 1.75 3.5 5.25索引位置不是整数时,使用最近位置的两个整数,加权计算来得到四分位的位置,每个整数的权重为距离的反比。加权计算: index = np.array([q1_index, q2_index, q3_index]) # 计算左边元素的值。 left = np.floor(index).astype(np.int8) # 计算右边元素的值。 right = np.ceil(index).astype(np.int8) # 获取index的小数部分与整数部分。 weight, _ = np.modf(index) # 根据左右两边的整数,加权计算四分位数的值。权重与距离成反比。 q = x[left] * (1 - weight) + x[right] * weight print(q) [ 8.25 16.5 20.75]当索引位置是整数时,计算过程可以简化为: x = np.array([1, 3, 10, 15, 18, 20, 21, 23, 40]) n = len(x) # 计算四分位的索引(index)。 index = (np.array([0.25, 0.5, 0.75])*(n - 1)).astype(np.int8) print(x[index]) [10, 18, 21] 反映离散程度的极差、方差和标准差极差指一组数据中,最大值与最小值之差。 方差体现的是一组数据中,每个元素与均值偏离的大小。 σ 2 = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) 2 \Huge{\sigma^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} σ2=n−11∑i=1n(xi−xˉ)2 x i x_i xi:数组中的每个元素。n:数组元素的个数。 x ˉ \bar{x} xˉ:数组中所有元素的均值。标准差为方差的开方。 σ = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) 2 \Huge{\sigma=\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}} σ=n−11∑i=1n(xi−xˉ)2 关于三者,说明如下: 极差的计算非常简单,但是极差没有充分的利用数据信息。方差(标准差)可以体现数据的分散性,方差(标准差)越大,数据越分散,方差(标准差)越小,数据越集中。方差(标准差)也可以体现数娼的波动性(稳定性)。方差(标准差)越大,数据波动性越大,方差(标淮差)越小,数据波动性越小。当数据较大时,也可以使用n代替n-1 # 计算极差。 sub = data["sepal_length"].max() - data["sepal_length"].min() # 计算方差。 var = data["sepal_length"].var() # 计算标准差。 std = data["sepal_length"].std() print(sub, var, std) 3.6000000000000005 0.6856935123042505 0.8280661279778629花瓣长度的方差较大,花瓣宽度的方差较小,绘图对比: plt.figure(figsize=(15, 4)) plt.ylim(-0.5, 1.5) plt.plot(data["petal_length"], np.zeros(len(data)), ls="", marker="o", ms=10, color="g", label="花瓣长度") plt.plot(data["petal_width"], np.ones(len(data)), ls="", marker="o", ms=10, color="r", label="花瓣宽度") plt.axvline(data["petal_length"].mean(), ls="--", color="g", label="花瓣长度均值") plt.axvline(data["petal_width"].mean(), ls="--", color="r", label="花瓣宽度均值") plt.legend()
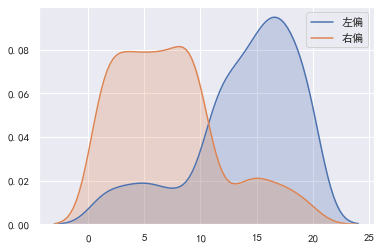
偏度是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。 如果数据对称分布(例如正态分布),则偏度为0。如果数据左偏分布.则偏度小于O。如果数据右偏分布.则偏度大于0。 # 构造左偏分布数据。 t1 = np.random.randint(1, 11, size=100) t2 = np.random.randint(11, 21, size=500) t3 = np.concatenate([t1, t2]) left_skew = pd.Series(t3) # 构造右偏分布数据。 t1 = np.random.randint(1, 11, size=500) t2 = np.random.randint(11, 21, size=100) t3 = np.concatenate([t1, t2]) right_skew = pd.Series(t3) # 计算偏度。 print(left_skew.skew(), right_skew.skew()) # 绘制核密度图。 sns.kdeplot(left_skew, shade=True, label="左偏") sns.kdeplot(right_skew, shade=True, label="右偏") plt.legend() -0.9911238058650503 0.7820903371872946
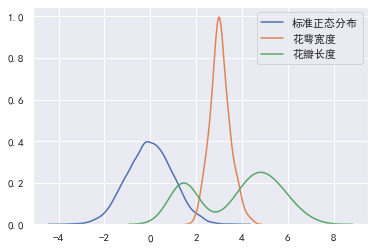
峰度是描述总体中所有取值分布形态陡缓程度的统计量。可以将峰度理解为数据分布的高矮程度。峰度的比较是相对于标准正态分布的。 对于标准正态分布,峰度为0.如果峰度大于0,则密度图高于标准正态分布。 数据在分布上比标准正态分布密集,方差(标淮羞)较小. 如果峰度小于0,则密度图低于标准正态分布。 说明数据在分布上比标准正态分布分散,方差(标准差)较大。 # 标准正态分布。 standard_normal = pd.Series(np.random.normal(0, 1, size=10000)) print("标准正态分布峰度:", standard_normal.kurt(), "标准差:", standard_normal.std()) print("花萼宽度峰度:", data["sepal_width"].kurt(), "标准差:", data["sepal_width"].std()) print("花瓣长度峰度:", data["petal_length"].kurt(), "标准差:", data["petal_length"].std()) sns.kdeplot(standard_normal, label="标准正态分布") sns.kdeplot(data["sepal_width"], label="花萼宽度") sns.kdeplot(data["petal_length"], label="花瓣长度") 标准正态分布峰度: 0.02338847301358893 标准差: 0.9980947521404823 花萼宽度峰度: 0.2907810623654279 标准差: 0.4335943113621737 花瓣长度峰度: -1.4019208006454036 标准差: 1.7644204199522617
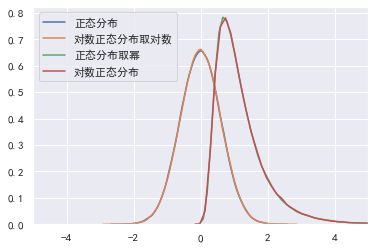
如果一个分布取对数后为正态分布,则该分布称为对数正态分布。 import random import numpy as np logdata = [random.lognormvariate(0, 0.6) for i in range(100000)] data = np.random.normal(0, 0.6, size=100000) sns.kdeplot(data, label="正态分布") sns.kdeplot(np.log(logdata), label="对数正态分布取对数") sns.kdeplot(np.exp(data), label="正态分布取幂") sns.kdeplot(logdata, label="对数正态分布") plt.xlim(-5, 5)
总体,就是被研究的全部数据,总体中的某个数据,就是个体。从总体中抽取部分个体.就构成了样本,样本中包含的个体数量,称为样本容量。 在实际的研究中,往往无法获取全部数据,只能对总体进行抽样。推断统计就是研究根据样本数据去推断总体数量特征的方法,它在对样本数据进行描述的基础上,对统计总体的未知数量特征做出以概率形式表述的推断,从而通过样本统计量来估计总体参数。 推断统计分析分为参数估计和假设检验。 参数估计 点估计与区间估计点估计,就是使用样本的统计量去代替总体参数。例如,我们要求鸢尾花的平均花瓣长度,就可以使用样本的均值来估计总体的均值: import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from sklearn.datasets import load_iris # 设置seaborn绘图的样式。 sns.set(style="darkgrid") plt.rcParams["font.family"] = "SimHei" plt.rcParams["axes.unicode_minus"] = False iris = load_iris() data = np.column_stack((iris.data, iris.target)) data = pd.DataFrame(data, columns=["sepal_length", "sepal_width", "petal_length", "petal_width", "type"]) print(data["petal_length"].mean()) 3.7586666666666693点估计实现简单,但是容易受到随机抽样的影响,无法保证结论的准确性。 区间估计则根据样本的统计量,计算出一个可能的区间与概率,表示总体的参数会有多少概率位于该区间中。区间估计指定的区间,我们称为置信区间,而区间估计指定的概率,称为置信度。例如,鸢尾花花瓣长度有70%的可能性在3.4cm-3.8cm之间,3.4cm- 3.8cm就是置信区间,而70%就是置信度。 总之,点估计是使用一个值来代替总体的参数值,能够给出具体的估计值但缺乏准确性。区间估计是使用的一个置信区间与置信度,表示总体参数有多少可能(置信度)会在该范围(置信区间)内,能够给出合理的范围和支持概率。 经过抽样,获取—个样本之后,该如何才能确定置信区间与置信度呢?区间估计的基石就是根据中心极限定理。 中心极限定理定理内容:如果总体(分布不重要)均值为μ,方差为 σ 2 \sigma^{2} σ2。我们进行随机抽样,样本容量为n,当n增大时,则样本均值逐渐趋近服从正态分布: X ˉ ∼ N ( μ , σ 2 / n ) \bar{X}\sim N\left(\mu, \sigma^{2} / n\right) Xˉ∼N(μ,σ2/n) 该定理说明了总体与样本之间,在分布上的联系。该定理说明在抽样的样本容量n足够大时,进行多次抽样.则每次抽样会得到—个均值,这些均值会围绕在总体均值左右,呈正态分布。均值等于总体的均值,标准差等于总体标准差 σ \sigma σ除以 n \sqrt{n} n 程序模拟 下面模拟总体的均值为30,标准差为80,抽样的样本容量n为64,看看1000次抽样的样本均值是否构成均值为30,标准差为10的正态分布: data = np.random.normal(30, 80, 100000) mean_arr = np.zeros(1000) for i in range(1000): mean_arr[i] = np.random.choice(data, size=64, replace=False).mean() print("均值:", np.mean(mean_arr)) print("标准差:", np.std(mean_arr), 80/np.sqrt(64)) print("偏度:", pd.Series(mean_arr).skew()) print("峰度:", pd.Series(mean_arr).kurt()) sns.distplot(mean_arr) 均值: 29.98515540795136 标准差: 10.387123594380887 10.0 偏度: -0.0499634202251343 峰度: 0.1875444656831493
从上述结果可以看到,样本的均值和标准差接近于理论值。 正态分布的特性
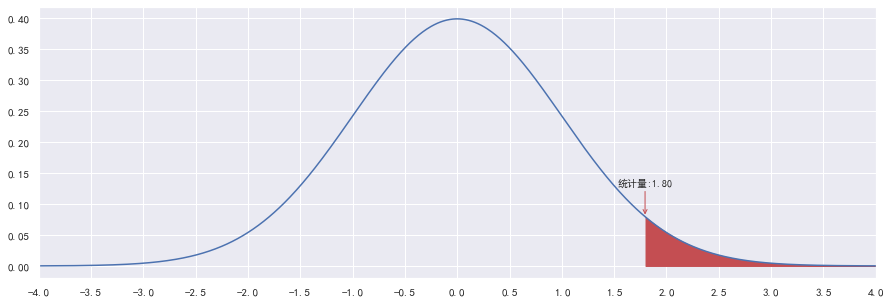
可以用程序模拟一下: scale = 50 x = np.random.normal(0, scale, size=10000000) for times in np.arange(1, 4): y = x[(x > -times * scale) & (x 1 times = arr[mid] rate = len(x[(x > -times * scale) & (x = confidenceLevel: high = mid - 1 else: low = mid + 1 iterations += 1 result = round(arr[low], 4) print(result, "迭代次数:", iterations) 2.5761 迭代次数: 17可以看到标准差大概是2.58倍时,正态分布覆盖99%样本数据。 可以通过scipy获取准确值: from scipy.stats import norm def calcTimes(confidenceLevel): alpha = 1 - confidenceLevel return norm.ppf(1 - alpha / 2) calcTimes(0.99)结果: 2.5758293035489004执行calcTimes(0.95)的结果是1.959963984540054,说明1.96倍标准差能覆盖95%的样本数据。 计算在正态分布情况下,指定倍数的标准差能覆盖多大比例的样本数据可以使用以下命令: from scipy.stats import norm # norm.cdf(x=?)计算正态分布概率(面积):P(X μ 0 \mu > \mu_{0} μ>μ0 则称这样的假设为右边假设检验(右边检验)。如果设立: 原假设: μ ≥ μ 0 \mu \geq \mu_{0} μ≥μ0备择假设: μ < μ 0 \mu < \mu_{0} μ μ 0 \mu > \mu_0 μ>μ0 设置显著性水平。 设置 α \alpha α= 0.05 根据问题选择假设检验的方式。 鸢尾花呈正态分布,总体标准差未知,选择 t t t检验。 计算统计量,并通过统计量获取 P P P值。计算下方红色部分(右边)的面积:
根据P值与α值,决定接受原假设还是备择假设。 P < α Pα,因此维持原假设,我们认为鸢尾花的平均花瓣确实长度不小于3.5cm 示例某公司要求,平均日投诉量均值不得超过1%。现检查—个部门的服务情况。在该部门维护的—个500人客户群中,近7天的投诉量分别为5, 6, 8, 4, 4, 7, 0。请问该部门是否达标? 原假设平均日投诉量均值小于等于1%,是个右边假设检验,总体标准差未知,样本量小于30,选择 t t t检验: data = np.array([5, 6, 8, 4, 4, 7, 0]) / 500 * 100 print(data) # 假设 平均日投诉量 |
【本文地址】
今日新闻 |
推荐新闻 |
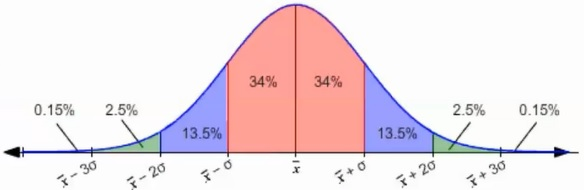 在正态分布中,数据的分布比例如下:
在正态分布中,数据的分布比例如下: