排序模型在工业界已经有了很长时间的历史，从基于策略规则的人工指定特征权值开始，发展到LR线性模型，LR+GBDT半自动特征组合模型，再到FM自动二阶特征组合模型及深度学习模型等不断发展。其中FM系列模型占据比较重要的位置，本篇文章就FM模型进行分析和总结。

FM系列模型2——DeepFM及python（DeepCTR）实现

在机器学习中，预测是一项基本的任务，所谓预测就是估计一个函数，该函数将一个n维的特征向量x映射到一个目标域T： D = { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( N ) , y ( N ) ) } D =\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(N)},y^{(N)})\} D={(x(1),y(1)),(x(2),y(2)),...,(x(N),y(N))}

在传统的线性模型中，每个特征都是独立的，如果需要考虑特征与特征之间的相互作用，可能需要人工对特征进行交叉组合。非线性SVM可以对特征进行核变换，但是在特征高度稀疏的情况下，并不能很好的进行学习。由于推荐系统是一个高度系数的数据场景，由此产生了FM系列算法，包括FM，FFM，DeepFM等算法。

推荐系统中还有一个比较重要的因素就是速度，比如容易并行，可解释、可拓展，这就是LR在工业界比较流行的原因之一。我们先回顾下线性模型和逻辑回归模型。

线性回归

y ^ ( x ) = w 0 + w 1 x 1 + w 2 x 2 + . . . + w n x n = w 0 + ∑ j = 1 n w i x i \begin{aligned} \hat{y}(x) = & w_0 + w_1x_1 + w_2x_2 + ...+ w_nx_n\\ =&w_0 + \sum_{j=1}^nw_ix_i \end{aligned} y^​(x)==​w0​+w1​x1​+w2​x2​+...+wn​xn​w0​+j=1∑n​wi​xi​​

逻辑回归 核心函数： h θ ( x ) = 1 1 + e − θ x h_{\theta}(x) = \frac{1}{1+e^{-\theta x}} hθ​(x)=1+e−θx1​ 对于一个样本：

P ( y = 1 ∣ x , θ ) = h θ ( x ) P ( y = 0 ∣ x , θ ) = 1 − h θ ( x ) \begin{aligned} P(y=1|x,\theta) =& h_{\theta}(x)\\ P(y=0|x,\theta) = &1-h_{\theta}(x) \end{aligned} P(y=1∣x,θ)=P(y=0∣x,θ)=​hθ​(x)1−hθ​(x)​ 那么进一步，样本x的概率表示为： P ( y ∣ x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) 1 − y P(y|x;\theta)=(h_{\theta}(x))^y(1-h_{\theta}(x))^{1-y} P(y∣x;θ)=(hθ​(x))y(1−hθ​(x))1−y 似然函数： L ( θ ) = ∏ i = 1 m P ( y ( i ) ∣ x ( i ) ; θ ) L(\theta) = \prod_{i=1}^mP(y^{(i)}|x^{(i)};\theta) L(θ)=i=1∏m​P(y(i)∣x(i);θ)

接下来，取对数，最大似然，最小loss： J ( θ ) = − 1 m l o g ( L ( θ ) ) J(\theta) = -\frac{1}{m}log(L(\theta)) J(θ)=−m1​log(L(θ)) 求导、梯度下降。。。

我们说线性模型有个非常大的问题就是没有考虑特征之间的相互关系：

y ^ ( x ) = w 0 + w 1 x 1 + w 2 x 2 + . . . + w n x n = w 0 + ∑ j = 1 n w i x i \begin{aligned} \hat{y}(x) = & w_0 + w_1x_1 + w_2x_2 + ...+ w_nx_n\\ =&w_0 + \sum_{j=1}^nw_ix_i \end{aligned} y^​(x)==​w0​+w1​x1​+w2​x2​+...+wn​xn​w0​+j=1∑n​wi​xi​​

事实上，如果特征之间相互关联，不同的特征组合可以提高模型的表达能力，而大多数情况下，特征之间都不是相互独立的。 为了表达这种关联特性，接下来，我们将函数 y ^ \hat{y} y^​改成： y ^ ( x ) = w 0 + ∑ j = 1 n w i x i + ∑ i = 1 n − 1 ∑ j = i + 1 n w i j x i x j \begin{aligned} \hat{y}(x) = &w_0 + \sum_{j=1}^nw_ix_i + \sum_{i=1}^{n-1}\sum_{j=i+1}^{n}w_{ij}x_ix_j \end{aligned} y^​(x)=​w0​+j=1∑n​wi​xi​+i=1∑n−1​j=i+1∑n​wij​xi​xj​​

这样两个特征之间的关系也考虑了，不过很遗憾，这种直接在 x i x i x_ix_i xi​xi​前面配上系数 w i j w_{ij} wij​的方式在稀疏数据面前有很大的缺陷。

在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练是很困难的。其原因是：每个参数 w i j w_ij wi​j的训练需要大量 x i x_i xi​和 x j x_j xj​非零样本，由于样本数据本来就比较稀疏，满 x i x_i xi​和 x j x_j xj​都非零的样本将会非常少。训练样本的不足，很容易导致参数 w i j w_{ij} wij​不准确，最终将严重影响模型的性能。一句话， W i j W_{ij} Wij​只有在观察样本中有 x i x_i xi​和 x j x_j xj​的情况下才能优化得到，对于观察样本中未出现过的特征分量不能进行相应参数的评估.

对于推荐系统来讲，高度稀疏的数据场景太普遍了。为了克服这个困难我们引入辅助向量：

V i = ( v i 1 , v i 2 , . . . , v i k ) T V_i = (v_{i1},v_{i2},...,v_{ik})^T Vi​=(vi1​,vi2​,...,vik​)T

将w改为： w ^ i j = V i T V j = ∑ l = 1 k v i l v j l \hat{w}_{ij}=V_i^TV_j=\sum_{l=1}^kv_{il}v_{jl} w^ij​=ViT​Vj​=l=1∑k​vil​vjl​

y ^ ( x ) = w 0 + ∑ j = 1 n w i x i + ∑ i = 1 n − 1 ∑ j = i + 1 n ( V i T V j ) x i x j \begin{aligned} \hat{y}(x) = &w_0 + \sum_{j=1}^nw_ix_i + \sum_{i=1}^{n-1}\sum_{j=i+1}^{n}(V_i^TV_j)x_ix_j \end{aligned} y^​(x)=​w0​+j=1∑n​wi​xi​+i=1∑n−1​j=i+1∑n​(ViT​Vj​)xi​xj​​

目前这样的表达式的复杂度是O(n^2)，但是我们可以对其进行分解，使得复杂度变为O(n)

二次项的参数数量减少为 k n kn kn个，远少于多项式模型的参数数量。另外，参数因子化使得 x h x i x_hx_i xh​xi​ 的参数和 x i x j x_ix_j xi​xj​ 的参数不再是相互独立的，因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说， x h x i x_hx_i xh​xi​ 和 $ x_ix_j$ 的系数分别为 v h , v i v_h,v_i vh​,vi​和 v i , v j v_i,v_j vi​,vj​ ，它们之间有共同项 v i v_i vi​ 。也就是说，所有包含“ x i x_i xi​ 的非零组合特征”（存在某个 j ≠ i j \not=i j​=i ，使得 x i x j ≠ 0 x_ix_j\not=0 xi​xj​​=0 ）的样本都可以用来学习隐向量 v i v_i vi​，这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中， w h i w_{hi} whi​ 和 w i j w_{ij} wij​是相互独立的。

到这里，我们就可以通过设置loss函数，梯度下降等方法进行优化了。

FFM是FM的升级版模型，引入了field的概念。FFM把相同性质的特征归于同一个field。在FFM中，每一维特征 x i x_i xi​，针对每一种field f j f_j fj​，都会学习到一个隐向量 V i , f j V_{i,f_j} Vi,fj​​，因此，隐向量不仅与特征相关，也与field相关。

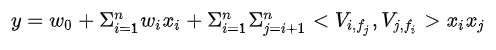设样本一共有n个特征, f 个field，那么FFM的二次项有nf个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看做FFM的特例，即把所有特征都归属到同一个field中。 如果隐向量的长度为k，那么FFM的二次项参数数量为nfk，远多于FM模型。此外由于隐向量与field相关，FFM二次项并不能够化简，时间复杂度为O(kn^2)。需要注意的是由于FFM中的latent vector只需要学习特定的field，所以通常 K F F M < < K F M K_{FFM}