数学建模:人口增长问题(基于指数增长模型和阻滞增长模型) |
您所在的位置:网站首页 › 指数方程例题 › 数学建模:人口增长问题(基于指数增长模型和阻滞增长模型) |
数学建模:人口增长问题(基于指数增长模型和阻滞增长模型)
|
数学建模:人口增长问题(基于指数增长模型和阻滞增长模型)
问题描述指数增长模型问题分析模型假设模型实现模型检验
阻滞增长模型问题分析问题假设模型实现模型检验
问题描述
利用下表人口数据做一个人口数量预测模型 年份1790180018101820183018401850186018701880人口数量3.95.37.29.612.917.123.231.438.650.21890190019101920193019401950196019701980199062.97692105.7122.8131.7150.7179.3203.2226.5248.720002010281.4308.7 指数增长模型 问题分析首先对数据进行可视化分析,我们以10年为间隔取一次人口数量,如果我们取样间隔过短可能会导致数值太过密集,导致不容易看出人口数量随时间的分布情况。通过对时间和人口数量作图得到下图。  图1
通过此图可以看出,人口数量和事件之间存在着指数关系,我们可以利用指数模型来预测人口。
模型假设
设
x
(
t
)
x(t)
x(t)为t时刻人口数量,且
x
(
t
)
x(t)
x(t)连续可微。人口增长率r为常量
模型实现
图1
通过此图可以看出,人口数量和事件之间存在着指数关系,我们可以利用指数模型来预测人口。
模型假设
设
x
(
t
)
x(t)
x(t)为t时刻人口数量,且
x
(
t
)
x(t)
x(t)连续可微。人口增长率r为常量
模型实现
记初始时刻(t=0时)人口数量为 x 0 x_0 x0,在 d t dt dt时间内人口增长 d x = r x d t dx=rxdt dx=rxdt。通过上述条件可以得到一个微分方程组: { d x d t = r x x ( 0 ) = x 0 \begin{cases} \small{\frac{dx}{dt}=rx}\\ x\left( 0 \right) =x_0\\ \end{cases} {dtdx=rxx(0)=x0 通过解上述微分方程得到 x ( t ) = x 0 e r t x(t)=x_0e^{rt} x(t)=x0ert,接下来通过最小二乘法法对参数 r , x 0 r,x_0 r,x0进行估计,将上面 x 与 t x与t x与t的关系两边取对数得到 y = r t + a , y = l n x , a = l n x 0 y=rt+a,y=lnx,a=lnx_0 y=rt+a,y=lnx,a=lnx0 根据人口数据(因为指数模型并不适合预测较长时期的人口,所以将1970年作为t=0),编程计算得到 r = 0.0196 , x 0 = 6.049 r=0.0196,x_0=6.049 r=0.0196,x0=6.049,代码如下 plot(t,x,'o'); xlabel('时间/年') ylabel('人口数量/亿') n=size(t,1); c = zeros(n,1)+1; t0 = [c,t]; y = log(x); B = inv(t0'*t0)*t0'*y; r=B(2); x0=exp(B(1)); f = @(t) x0*exp(r*t); hold on; fplot(f,[0,220]);得到结果图为  图2
模型检验
图2
模型检验
计算MSE得到 M S E = 2.1 ∗ 1 0 3 MSE=2.1*10^{3} MSE=2.1∗103,计算代码如下 x_hat = f(t); mse = (x - x_hat)'*(x - x_hat)/n;计算得到MSE较大,因为我们所使用的数据数值较大,所以计算某一年预测值的相对误差的结果更有说服力。 计算在2000年的相对误差 e r r o r = ∣ x _ h a t ( 2000 ) − x ( 2000 ) ∣ x ( 2000 ) = 0.38 error=\small{\frac{\left| x\_hat\left( 2000 \right) -x\left( 2000 \right) \right|}{x\left( 2000 \right)}}=0.38 error=x(2000)∣x_hat(2000)−x(2000)∣=0.38,emm…可以看出普通指数模型不是特别好。 阻滞增长模型 问题分析观察图2可以发现,人口的变化率 r r r并不是不变的,因为资源受限等问题,人口变化率 r r r随着人口数量的增加而减少,成反比例关系,这说明我们在上面的假设中出现了错误,所以要更改假设内容。 问题假设 人口变化率 r r r与人口数量 x x x成反比例变化关系,即 r = r 0 − k x r=r_0-kx r=r0−kx人口数量受环境影响,人口最大承受量为 x m x_m xm设 x ( t ) x(t) x(t)为t时刻人口数量,且 x ( t ) x(t) x(t)连续可微。 模型实现由假设可知 x = x m x=x_m x=xm时, r = r 0 − k x m = 0 r=r_0-kx_m=0 r=r0−kxm=0 解出 k = r 0 x m k=\frac{r_0}{x_m} k=xmr0,可以得到下列方程组: { d x d t = r x ( 1 − x x m ) x ( 0 ) = x 0 \begin{cases} \frac{dx}{dt}=rx(1-\frac{x}{x_m})\\ x(0)=x_0\\ \end{cases} {dtdx=rx(1−xmx)x(0)=x0 参数估计 一、非线性最小二乘估计 通过解上述微分方程得到 x ( t ) = x m 1 + ( x m x 0 − 1 ) e − r t x\left( t \right) =\frac{x_m}{1+\left( \small{\frac{x_m}{x_0}-1} \right) e^{-rt}} x(t)=1+(x0xm−1)e−rtxm 利用matlab拟合工具箱拟合得到 r = 0.02681 , x m = 370 r=0.02681,x_m=370 r=0.02681,xm=370.结果如下图 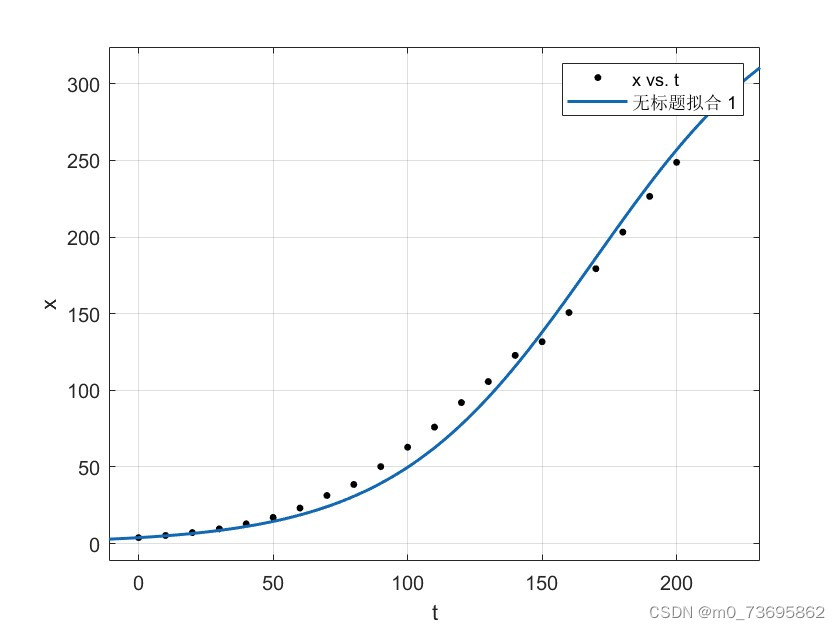 图3
可以观察到结果与指数增长模型比较啊v的了较好效果。
二、线性最小二乘估计
图3
可以观察到结果与指数增长模型比较啊v的了较好效果。
二、线性最小二乘估计
对上面的微分方程进行变换得到 1 x d x d t = r − r x m x \frac{1}{x}\frac{dx}{dt}=r-\frac{r}{x_m}x x1dtdx=r−xmrx为线性关系,可以利用线性最小二乘法拟合。利用matlab拟合得到 r = 0.0288 , x m = 299.439 r=0.0288,x_m=299.439 r=0.0288,xm=299.439,代码如下: figure(2); plot(t,x,'o'); xlabel('时间/年') ylabel('人口数量/亿') hold on; dx = diff(x)/10; y = dx./x(2:end); t = t(2:end); c = zeros(n-1,1)+1; t0 = [c,t]; B = inv(t0'*t0)*t0'*y; r=B(1); xm = -B(1)/B(2); f2 = @(z) xm/(1+(xm/3.9-1)*exp(-r*z)); fplot(f2,[0,220]);结果图:  图4
通过观察图3和图4可以看出图3的效果要好于图4的效果,因为图4在计算微分时并不是实际的微分而是利用以10年为间隔的差分。所以拟合效果较差。
模型检验
图4
通过观察图3和图4可以看出图3的效果要好于图4的效果,因为图4在计算微分时并不是实际的微分而是利用以10年为间隔的差分。所以拟合效果较差。
模型检验
在模型检验时利用非线性最小二乘估计的参数作为最终的参数。还是和模型一一样利用2000年的人口数量进行检验。得到相对误差为 1.6 % 1.6\% 1.6%。可以看出解出的模型效果不错。 |
【本文地址】
今日新闻 |
推荐新闻 |