指数函数 |
您所在的位置：网站首页 › 指数函数的求法 › 指数函数 |
指数函数
 「Exp」重定向至此。关于複雜度类，请见「EXPTIME」。关于遊戲術語，请见「经验值」。
 指数函数对于
x
{\displaystyle x}
的负数值非常平坦，对于
x
{\displaystyle x}
的正数值迅速攀升，在
x
{\displaystyle x}
等于
0
{\displaystyle 0}
的时候等于
1
{\displaystyle 1}
。它的
y
{\displaystyle y}
值总是等于在这一点上的斜率。
指数函数（英語：Exponential function）是形式為 b x {\displaystyle b^{x}} 的數學函数，其中 b {\displaystyle b} 是底數（或稱基數，base），而 x {\displaystyle x} 是指數（index / exponent）。 現今指數函數通常特指以 e {\displaystyle {\mbox{e}}} 為底數的指數函數（即 e x {\displaystyle {\mbox{e}}^{x}} ），為数学中重要的函数，也可寫作 exp ( x ) {\displaystyle \exp(x)} 。这里的 e {\displaystyle {\mbox{e}}} 是数学常数，也就是自然对数函数的底数，近似值为 2.718281828 {\displaystyle 2.718281828} ，又称为欧拉数。 作为实数变量 x {\displaystyle x} 的函数， y = e x {\displaystyle y={\mbox{e}}^{x}} 的图像总是正的（在 x {\displaystyle x} 轴之上）并递增（从左向右看），它不触及 x {\displaystyle x} 轴，尽管它可以任意程度的靠近它，即 x {\displaystyle x} 轴是这个图像的水平渐近线。一般的说，变量 x {\displaystyle x} 可以是任何实数或复数，甚至是完全不同种类的数学对象。它的反函数是定义在所有正数 x {\displaystyle x} 上的自然对数 ln x {\displaystyle \ln {x}} 。 本文集中于带有底数为欧拉数 e {\displaystyle {\mbox{e}}} 的指数函数。有时，特别是在科学中，术语指数函数更一般性的用于形如 k b x {\displaystyle kb^{x}} 的函数，这里的 b {\displaystyle b} 称为底数，是不等于 1 {\displaystyle 1} 的任何正实数。 目录 1 概要 2 形式定义 3 性质 4 导数和微分方程 5 '"`UNIQ--postMath-00000062-QINU`"'的连分数 6 在複平面上 7 矩阵和巴拿赫代数 8 在李代数上 9 註釋與引用 9.1 证明 10 外部链接 11 参见 概要[编辑]最简单的說，指数函数按恒定速率翻倍。例如细菌培养时细菌总数（近似的）每三个小时翻倍，和汽车的价值每年减少10%都可以被表示为一个指数。特別是複利，事實上就是它導致了雅各布·伯努利在1683年介入了現在叫做 e {\displaystyle e} 的數[1]： lim n → ∞ ( 1 + 1 n ) n {\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}後來約翰·伯努利在1697年研究了指數函數的微積分。[1] 設1份借貸有 x {\displaystyle x} 利率，逐月複利話，則每月增加當前值的 x 12 {\displaystyle {\frac {x}{12}}} 倍，每月總值都要乘以 ( 1 + x 12 ) {\displaystyle (1+{\frac {x}{12}})} ，一年的總值為 ( 1 + x 12 ) 12 {\displaystyle (1+{\frac {x}{12}})^{12}} ，逐日複利的話，就是 ( 1 + x 365 ) 365 {\displaystyle (1+{\frac {x}{365}})^{365}} [2]。設年中時段數可為無限，則有如下最初由歐拉提出[3]的指數函數定義： exp ( x ) = lim n → ∞ ( 1 + x n ) n {\displaystyle \exp(x)=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}指數函數有基本的指數恆等式， exp ( x + y ) = exp ( x ) ⋅ exp ( y ) {\displaystyle \exp(x+y)=\exp(x)\cdot \exp(y)}這是它寫為 e x {\displaystyle e^{x}} 的原因[4]。 在雅各布·伯努利之前，約翰·納皮爾在1614年[5]以及Jost Bürgi在6年後[6]，分別發表了獨立編制的對數表，當時通過對接近1的底數的大量乘冪運算，來找到指定範圍和精度的對數和所對應的真數，當時還沒出現有理數冪的概念，直到1742年William Jones才發表了現在的冪指數概念[7]。按後世的觀點，Jost Bürgi的底數1.000110000相當接近自然對數的底數 e {\displaystyle e} ，而約翰·納皮爾的底數0.999999910000000相當接近 1 e {\displaystyle {\frac {1}{e}}} [8]。實際上不需要做開高次方這種艱難運算，約翰·納皮爾用了20年時間進行相當於數百萬次乘法的計算，Henry Briggs（英语：Henry Briggs (mathematician)）建議納皮爾改用10為底數未果，他用自己的方法[9]於1624年部份完成了常用對數表的編制。 形式定义[编辑] 指数函数（蓝色），幂级数的前n+1项的和（红色）。
指数函数 e x {\displaystyle e^{x}} 可以用各种等价的方式定义。特别是它可以定义为幂级数： e x = 1 + ∑ n = 1 ∞ x n n ! = 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! + ⋯ {\displaystyle e^{x}=1+\sum _{n=1}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots }或序列的极限： e x = lim n → ∞ ( 1 + x n ) n . {\displaystyle e^{x}=\lim _{n\to \infty }\left(1+{x \over n}\right)^{n}.}在这些定义中， n ! {\displaystyle n!} 表示 n {\displaystyle n} 的阶乘，而 x {\displaystyle x} 可以是任何实数、复数、和巴拿赫代数的元素。 設 x ≥ 0 {\displaystyle x\geq 0} 是確定的非負實數。定義 t n = ( 1 + x n ) n , s n = ∑ k = 0 n x k k ! . {\displaystyle t_{n}=\left(1+{\frac {x}{n}}\right)^{n},\ s_{n}=\sum _{k=0}^{n}{\frac {x^{k}}{k!}}.}據二項式定理， t n = ∑ k = 0 n ( n k ) x k n k = 1 + x + ∑ k = 2 n n ( n − 1 ) ( n − 2 ) ⋯ [ n − ( k − 1 ) ] x k k ! n k = 1 + x + x 2 2 ! ( 1 − 1 n ) + x 3 3 ! ( 1 − 1 n ) ( 1 − 2 n ) + ⋯ ⋯ + x n n ! ( 1 − 1 n ) ⋯ ( 1 − n − 1 n ) ≤ s n {\displaystyle {\begin{aligned}t_{n}&=\sum _{k=0}^{n}{n \choose k}{\frac {x^{k}}{n^{k}}}=1+x+\sum _{k=2}^{n}{\frac {n(n-1)(n-2)\cdots [n-(k-1)]x^{k}}{k!\,n^{k}}}\\[8pt]&=1+x+{\frac {x^{2}}{2!}}\left(1-{\frac {1}{n}}\right)+{\frac {x^{3}}{3!}}\left(1-{\frac {1}{n}}\right)\left(1-{\frac {2}{n}}\right)+\cdots \\[8pt]&{}\qquad \cdots +{\frac {x^{n}}{n!}}\left(1-{\frac {1}{n}}\right)\cdots \left(1-{\frac {n-1}{n}}\right)\leq s_{n}\end{aligned}}}（設 x ≥ 0 {\displaystyle x\geq 0} 得到最終的不等式）故此 lim sup n → ∞ t n ≤ lim sup n → ∞ s n = e x {\displaystyle \limsup _{n\to \infty }t_{n}\leq \limsup _{n\to \infty }s_{n}=e^{x}}可證明當 n {\displaystyle n} 趨於無限大時上述二定義等價。这些定义的进一步解释和它们的等价性的证明，参见文章指数函数的特征描述（英语：Characterizations of the exponential function）。 性质[编辑]
y
=
b
x
{\displaystyle y=b^{x}}
對各種底數b的圖像，分別為綠色的10、紅色的
e
{\displaystyle e}
、藍色的2和青色的
1
2
{\displaystyle {\frac {1}{2}}}
。
從指数函数的定義： e x = lim n → ∞ ( 1 + x n ) n {\displaystyle e^{x}=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}可得出它有冪運算的“指数定律”： e 0 = 1 {\displaystyle \!\,e^{0}=1} e 1 = e {\displaystyle \!\,e^{1}=e} e x + y = e x e y {\displaystyle \!\,e^{x+y}=e^{x}e^{y}} e x y = ( e x ) y {\displaystyle \!\,e^{xy}=\left(e^{x}\right)^{y}} e − x = 1 e x {\displaystyle \!\,e^{-x}={1 \over e^{x}}}它们对所有实数 x {\displaystyle x} 与 y {\displaystyle y} 都是有效的。 因為在指數函數的定義中 x {\displaystyle x} 是實數，可以使用自然对数，把更一般的指数函数，即正實數的實數冪函數定义為 b x = ( e ln b ) x = e x ln b . {\displaystyle \!\,b^{x}=(e^{\ln b})^{x}=e^{x\ln b}.}定义于所有的 b > 0 {\displaystyle b>0} ，和所有的实数 x {\displaystyle x} 。它叫做“底数为 b {\displaystyle b} 的指数函数”。從而拓展了通過乘方和方根運算定義的正實數的有理數冪函數： b m n = b m n . {\displaystyle b^{\frac {m}{n}}={\sqrt[{n}]{b^{m}}}.}而方根運算可通過自然對數和指數函數來表示（单位根） x n = x 1 n = e ln x n . {\displaystyle {\sqrt[{n}]{x}}=x^{\frac {1}{n}}=e^{\frac {\ln x}{n}}.}介入數 e {\displaystyle e} 的根本動機，特別是在微積分中，是通過指數函數和對數來進行導數和積分運算。[10] 一般指數函數 y = b x {\displaystyle y=b^{x}} 有極限形式的導數: d d x b x = lim h → 0 b x + h − b x h = lim h → 0 b x b h − b x h = b x ( lim h → 0 b h − 1 h ) . {\displaystyle {\frac {d}{dx}}b^{x}=\lim _{h\to 0}{\frac {b^{x+h}-b^{x}}{h}}=\lim _{h\to 0}{\frac {b^{x}b^{h}-b^{x}}{h}}=b^{x}\left(\lim _{h\to 0}{\frac {b^{h}-1}{h}}\right).}最右端的極限無關於變量 x {\displaystyle x} ：它依賴於底數 b {\displaystyle b} 而是常量[11]。根據求導的鏈式法則： d d x ( 1 + x n ) n = ( 1 + x n ) n − 1 . {\displaystyle {\frac {d}{dx}}\left(1+{\frac {x}{n}}\right)^{n}=\left(1+{\frac {x}{n}}\right)^{n-1}.}當這個底數是 e {\displaystyle e} 時[4]，這個常量等於1[12]，因此有: d d x e x = e x . {\displaystyle {\frac {d}{dx}}e^{x}=e^{x}.} 导数和微分方程[编辑]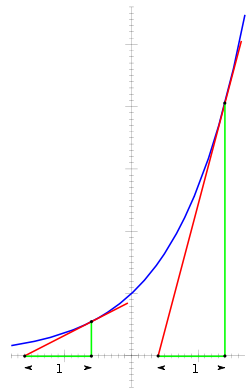 指數函數的導數等於這個函數的值。從在藍色曲線上任意一點
P
{\displaystyle P}
，繪製紅色切線，和高度為
h
{\displaystyle h}
的垂直豎線，與在
x
{\displaystyle x}
軸上的底邊
b
{\displaystyle b}
形成了一個直角三角形。因為在
P
{\displaystyle P}
上的紅色切線的斜率（導數）等於這個三角形的高度與底邊長度的比，而導數等於這個函數的值，
h
{\displaystyle h}
必須等於
h
{\displaystyle h}
與
b
{\displaystyle b}
之比。因此底邊
b
{\displaystyle b}
必須總是
1
{\displaystyle 1}
。
指数函数在数学和科学中的重要性主要源于它的导数的性质。特别是 d d x e x = e x {\displaystyle {d \over dx}e^{x}=e^{x}}就是说， e x {\displaystyle e^{x}} 是它自己的导数。这可以用泰勒级数证明： d d x e x = d d x ( 1 + ∑ n = 1 ∞ x n n ! ) = ∑ n = 1 ∞ n x n − 1 n ! = ∑ n = 1 ∞ x n − 1 ( n − 1 ) ! = ∑ k = 0 ∞ x k k ! , where k = n − 1 = e x {\displaystyle {\begin{aligned}{\frac {d}{dx}}e^{x}&={\frac {d}{dx}}\left(1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}\right)=\sum _{n=1}^{\infty }{\frac {nx^{n-1}}{n!}}=\sum _{n=1}^{\infty }{\frac {x^{n-1}}{(n-1)!}}\\[6pt]&=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}},{\text{ where }}k=n-1\\[6pt]&=e^{x}\end{aligned}}}对于常数 K {\displaystyle K} 的形如 K e x {\displaystyle Ke^{x}} 的函数是唯一有这个性质的函数（这得出自皮卡-林德洛夫定理[13]）。其他等价说法有： 函数的图像的在任何一点上的斜率是这个函数在这一点上的高度。 函数在 x {\displaystyle x} 的增长速率等于在这个函数在 x {\displaystyle x} 上的值。 这个函数是微分方程 y ′ = y {\displaystyle y'=y} 的解。 exp是泛函导数的不动点。事实上，很多不同的方程引發指数函数，包括薛定谔方程和拉普拉斯方程和简单谐波运动的方程。 对于有其他底数的指数函数： d d x b x = ( ln b ) b x {\displaystyle {d \over dx}b^{x}=(\ln b)b^{x}}所以任何指数函数都是它自己导数的常数倍。 如果一个变量的增长或衰减速率是与它的大小成比例的，比如在无限制情况下的人口增长、复利和放射性衰变，则这个变量可以写为常数倍的时间的指数函数。 进一步的，对任何可微函数 f ( x ) {\displaystyle f(x)} ，我们可以通过链式法则找到： d d x e f ( x ) = f ′ ( x ) e f ( x ) {\displaystyle {d \over dx}e^{f(x)}=f'(x)e^{f(x)}} . e x {\displaystyle e^{x}} 的连分数[编辑]通过歐拉連分數公式得到 e x {\displaystyle e^{x}} 的連分數： e x = 1 + x 1 − x x + 2 − 2 x x + 3 − 3 x x + 4 − ⋱ {\displaystyle e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-\ddots }}}}}}}}}e z {\displaystyle e^{z}} 的廣義連分數收斂更快速:[14] e z = 1 + 2 z 2 − z + z 2 6 + z 2 10 + z 2 14 + ⋱ {\displaystyle e^{z}=1+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{10+{\cfrac {z^{2}}{14+\ddots }}}}}}}}}或者，替換 z = x y {\displaystyle z={\frac {x}{y}}} : e x y = 1 + 2 x 2 y − x + x 2 6 y + x 2 10 y + x 2 14 y + ⋱ {\displaystyle e^{\frac {x}{y}}=1+{\cfrac {2x}{2y-x+{\cfrac {x^{2}}{6y+{\cfrac {x^{2}}{10y+{\cfrac {x^{2}}{14y+\ddots }}}}}}}}}有特殊情況 z = 2 {\displaystyle z=2} : e 2 = 1 + 4 0 + 2 2 6 + 2 2 10 + 2 2 14 + ⋱ = 7 + 2 5 + 1 7 + 1 9 + 1 11 + ⋱ {\displaystyle e^{2}=1+{\cfrac {4}{0+{\cfrac {2^{2}}{6+{\cfrac {2^{2}}{10+{\cfrac {2^{2}}{14+\ddots \,}}}}}}}}=7+{\cfrac {2}{5+{\cfrac {1}{7+{\cfrac {1}{9+{\cfrac {1}{11+\ddots \,}}}}}}}}} 在複平面上[编辑] 指數函數
e
z
{\displaystyle e^{z}}
可以定義為
(
1
+
z
n
)
n
{\displaystyle (1+{\frac {z}{n}})^{n}}
在
n
{\displaystyle n}
趨於無窮時的極限。在本動畫中，
z
=
i
π
3
{\displaystyle z={\frac {i\pi }{3}}}
而
n
{\displaystyle n}
選取從1增到100的各種值。
(
1
+
z
n
)
n
{\displaystyle (1+{\frac {z}{n}})^{n}}
的計算顯示為在複平面上
n
{\displaystyle n}
次乘法的組合效果。隨著
n
{\displaystyle n}
變大，這些點趨近於複平面單位圓，覆及
π
3
{\displaystyle {\frac {\pi }{3}}}
弧度的角度。
如同在實數情況下，在複平面的指數函數可以用多種等價方式定義。比如冪級數形式的: e z = ∑ n = 0 ∞ z n n ! {\displaystyle e^{z}=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}}或者序列的極限： e z = lim n → ∞ ( 1 + z n ) n {\displaystyle e^{z}=\lim _{n\rightarrow \infty }\left(1+{\frac {z}{n}}\right)^{n}}它带有虚数周期 2 π i {\displaystyle 2\pi i} [prove 1]，它可以写为 e a + b i = e a ( cos b + i sin b ) {\displaystyle \!\,e^{a+bi}=e^{a}(\cos b+i\sin b)}这里的 a {\displaystyle a} 和 b {\displaystyle b} 是实数值。参见欧拉公式，这个公式把指数函数和三角函数与指數函数联系起来。 在考虑定义在複平面上的函数的时候，指数函数拥有重要的性质 e z + w = e z e w {\displaystyle \!\,e^{z+w}=e^{z}e^{w}} e 0 = 1 {\displaystyle \!\,e^{0}=1} e z ≠ 0 {\displaystyle \!\,e^{z}\neq 0} d d z e z = e z {\displaystyle \!\,{d \over dz}e^{z}=e^{z}} ( e z ) n = e n z , n ∈ Z {\displaystyle \,(e^{z})^{n}=e^{nz},n\in \mathbb {Z} }对于所有的 z {\displaystyle z} 和 w {\displaystyle w} 。 它是周期的全纯函数。我们看到除了多项式的所有初等函数都以某种方式起源于指数函数。 扩展自然对数到復平面上的多值函数 ln z {\displaystyle \ln z} ，我们可以接着定义更一般性的指数函数： z w = e w ln z {\displaystyle \!\,z^{w}=e^{w\ln z}}对于所有复数 z {\displaystyle z} 和 w {\displaystyle w} ，这也是多值函数，即使是在 z {\displaystyle z} 為實數的情況下。前面關於正實數情況下的指數乘積規則在多值函數情況下必須改為: ( e z ) w ≠ e z w {\displaystyle (e^{z})^{w}\neq e^{zw}} ，而是 ( e z ) w = e ( z + 2 π i n ) w {\displaystyle (e^{z})^{w}=e^{(z+2\pi in)w}\,} 多值於整數n 之上。指数函数把在複平面上任何直线映射到在複平面中以原点为中心的对数螺线。要注意两个特殊情况：当最初的线平行于实轴的时候，结果的螺线永不遮盖（close in on）自身；当最初的线平行于虚轴的时候，结果的螺线是某个半径的圆。 在複平面上指数函数（主支）
z = Re(ex+iy) 
z = Im(ex+iy) 
矩阵和巴拿赫代数[编辑]
上面给出的指数函数的定义可以用于所有巴拿赫代数，特别是对于方块矩阵（在这种情况函数叫做矩阵指数）。在这种情况下我们有 e x + y = e x e y if x y = y x {\displaystyle \ e^{x+y}=e^{x}e^{y}{\mbox{ if }}xy=yx} e 0 = 1 {\displaystyle \ e^{0}=1} e x {\displaystyle \ e^{x}} 与 e − x {\displaystyle \ e^{-x}} 是互倒的 e x {\displaystyle \ e^{x}} 在点 x {\displaystyle \ x} 的导数是从 u {\displaystyle \ u} 到 u e x {\displaystyle \ ue^{x}} 的线性映射。在非交换巴拿赫代数的上下文中，比如矩阵代数或在巴拿赫空间或希尔伯特空间上的算子，指数函数经常被认做实数参数的函数： f ( t ) = e t A {\displaystyle \ f(t)=e^{tA}}这里的A是这个代数的固定元素而t是任何实数。这个函数有重要的性质 f ( s + t ) = f ( s ) f ( t ) {\displaystyle \ f(s+t)=f(s)f(t)} f ( 0 ) = 1 {\displaystyle \ f(0)=1} f ′ ( t ) = A f ( t ) {\displaystyle \ f'(t)=Af(t)} 在李代数上[编辑]从李代数到李群的“指数映射”有着上述性质。事实上因为R是带有乘法的所有正实数的李群的李代数，实数参数的常规指数函数是李代数下的特殊情况。类似的，因为所有方块实数矩阵的李代数M (n, R)属于所有正可逆方块矩阵的李群，方块矩阵的指数函数是李代数指数映射的特殊情况。 註釋與引用[编辑] ^ 1.0 1.1 John J O'Connor; Edmund F Robertson. The number e. School of Mathematics and Statistics. University of St Andrews, Scotland. [2011-06-13]. （原始内容存档于2015-09-08）. ^ 假定利率為100%，借期1年本息合為200%，利息平均每月約8.3%。按複利可以只借1個月，1個月未能還款，本息合計為借款，如此1年下來本息合計約為261.3%。如果借貸者能在1個月內歸還，則不需要付1整年的利息，放貸者快速收回資金可以借給他人；拖到1年歸還，放貸者得到比正常放貸1年要高的利息；1年後按複利計算本息快速增長，借貸者可能就還不起了，而放貸者獲得抵押品。甚至可以逐日借款，這樣1年的收益高於261.3%，但增大不多，而借貸者可以更快還清少付利息，e 就是設立更小還款時限增加獲利，能達到的1年極限收益，即約為 271.8%。應區分抵押貸款和高利貸。 ^ Eli Maor, e: the Story of a Number, p.156. ^ 4.0 4.1 lim n → ∞ ( 1 + x n ) n = lim n → ∞ ( ( 1 + 1 n ) n ) x {\displaystyle \lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}=\lim _{n\to \infty }\left(\left(1+{\frac {1}{n}}\right)^{n}\right)^{x}} 前者成為定義因其有導數上的重要性質。 ^ Ernest William Hobson, John Napier and the invention of logarithms, 1614, Cambridge: The University Press, 1914 ^ Boyer, Carl B., 14, section "Jobst Bürgi", A History of Mathematics, New York: John Wiley & Sons, 1991, ISBN 978-0-471-54397-8 ^ ( 1 + 1 n ) x = ( ( 1 + 1 n ) n ) x n {\displaystyle \left(1+{\frac {1}{n}}\right)^{x}=\left(\left(1+{\frac {1}{n}}\right)^{n}\right)^{\frac {x}{n}}} 在最初的概念下，底數是接近1的數，而對數是整數；經過簡單變換後，底數變大了，成為接近數學常量e的數，而對數變小了，成為 x/n。 ^ 選取接近e的底數b，對數表涉及的bx為單調增函數，定義域為0到1而值域為1到b；選取接近1/e的底數b，對數表涉及的bx為單調減函數，定義域為0到∞而值域為1到0。 ^ 以 10 1 2 54 {\displaystyle 10^{\frac {1}{2^{54}}}} 這個接近1的數為基礎。 ^ Kline, M. (1998) Calculus: An intuitive and physical approach, section 12.3 "The Derived Functions of Logarithmic Functions." （页面存档备份，存于互联网档案馆）, pp. 337 ff, Courier Dover Publications, 1998, ISBN 0-486-40453-6 ^ lim h → 0 ( b h − 1 ) 1 h = lim 1 n → 0 ( b 1 n − 1 ) n = lim n → ∞ n ( b 1 / n − 1 ) = ln ( b ) . {\displaystyle {\begin{aligned}\lim _{h\to 0}\left(b^{h}-1\right){\frac {1}{h}}&=\lim _{{\frac {1}{n}}\to 0}\left(b^{\frac {1}{n}}-1\right)n\\&=\lim _{n\rightarrow \infty }n(b^{1/n}-1)\\&=\ln(b).\\\end{aligned}}} 這裡的自然對數定義為歐拉提出，是他定義的指數函數的逆函數。 ^ d d x ( 1 + x n ) n = n n + x ( 1 + x n ) n . {\displaystyle {\frac {d}{dx}}\left(1+{\frac {x}{n}}\right)^{n}={\frac {n}{n+x}}\left(1+{\frac {x}{n}}\right)^{n}.} 這個函數的導數與函數值的比為 n/(n+x)，當n→∞時， n/(n+x)=1，等式兩端就是指數函數的導數和指數函數。 ^ 通过 y ( t ) = e t , y ( 0 ) = K {\displaystyle y(t)=e^{t},y(0)=K} 和 f ( t , y ( t ) ) = y ( t ) {\displaystyle f(t,y(t))=y(t)} 。 ^ "A.2.2 The exponential function." L. Lorentzen and H. Waadeland, Continued Fractions, Atlantis Studies in Mathematics, page 268.. [2014-03-11]. （原始内容存档于2021-03-08）. 证明[编辑] ^ e i π = lim n → ∞ ( 1 + π n i ) n {\displaystyle e^{i\pi }=\lim _{n\rightarrow \infty }\left(1+{\frac {\pi }{n}}i\right)^{n}} 為 ( 1 + π n i ) n {\displaystyle \left(1+{\frac {\pi }{n}}i\right)^{n}} 的極限形式：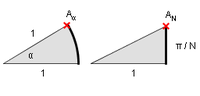
8個三角形 
16個三角形 
eiπ+1=0 故有歐拉恆等式： e i π + 1 = 0. {\displaystyle e^{i\pi }+1=0.\,\!} 外部链接[编辑] Complex exponential function. PlanetMath. 埃里克·韦斯坦因. Exponential Function. MathWorld. Complex Exponential Function Module by John H. Mathews Taylor Series Expansions of Exponential Functions （页面存档备份，存于互联网档案馆） at efunda.com （页面存档备份，存于互联网档案馆） Complex exponential interactive graphic （页面存档备份，存于互联网档案馆） 参见[编辑] 指数函数的特征描述 指数增长、指數衰減 对数 幂与幂定律 迭代冪次 古德温 - 斯塔顿积分 规范控制
GND: 4382956-9
|
的负数值非常平坦，对于
x
{\displaystyle x}
的时候等于
1
{\displaystyle 1}
。它的
y
{\displaystyle y}
值总是等于在这一点上的斜率。
的數學函数，其中
b
{\displaystyle b}
是底數（或稱基數，base），而
x
{\displaystyle x}
為底數的指數函數（即
e
x
{\displaystyle {\mbox{e}}^{x}}
），為数学中重要的函数，也可寫作
exp
(
x
)
{\displaystyle \exp(x)}
。这里的
e
{\displaystyle {\mbox{e}}}
，又称为欧拉数。
的图像总是正的（在
x
{\displaystyle x}
。
的函数，这里的
b
{\displaystyle b}
的數[1]：
倍，每月總值都要乘以
(
1
+
x
12
)
{\displaystyle (1+{\frac {x}{12}})}
，一年的總值為
(
1
+
x
12
)
12
{\displaystyle (1+{\frac {x}{12}})^{12}}
，逐日複利的話，就是
(
1
+
x
365
)
365
{\displaystyle (1+{\frac {x}{365}})^{365}}
[2]。設年中時段數可為無限，則有如下最初由歐拉提出[3]的指數函數定義：
的原因[4]。
[8]。實際上不需要做開高次方這種艱難運算，約翰·納皮爾用了20年時間進行相當於數百萬次乘法的計算，Henry Briggs（英语：Henry Briggs (mathematician)）建議納皮爾改用10為底數未果，他用自己的方法[9]於1624年部份完成了常用對數表的編制。
表示
n
{\displaystyle n}
的阶乘，而
x
{\displaystyle x}
是確定的非負實數。定義
![{\begin{aligned}t_{n}&=\sum _{{k=0}}^{n}{n \choose k}{\frac {x^{k}}{n^{k}}}=1+x+\sum _{{k=2}}^{n}{\frac {n(n-1)(n-2)\cdots [n-(k-1)]x^{k}}{k!\,n^{k}}}\\[8pt]&=1+x+{\frac {x^{2}}{2!}}\left(1-{\frac {1}{n}}\right)+{\frac {x^{3}}{3!}}\left(1-{\frac {1}{n}}\right)\left(1-{\frac {2}{n}}\right)+\cdots \\[8pt]&{}\qquad \cdots +{\frac {x^{n}}{n!}}\left(1-{\frac {1}{n}}\right)\cdots \left(1-{\frac {n-1}{n}}\right)\leq s_{n}\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8451a7eb4b301928aa74f4e3565fc942cf9d6c34)
對各種底數b的圖像，分別為綠色的10、紅色的
e
{\displaystyle e}
。
e
1
=
e
{\displaystyle \!\,e^{1}=e}
e
x
+
y
=
e
x
e
y
{\displaystyle \!\,e^{x+y}=e^{x}e^{y}}
e
x
y
=
(
e
x
)
y
{\displaystyle \!\,e^{xy}=\left(e^{x}\right)^{y}}
e
−
x
=
1
e
x
{\displaystyle \!\,e^{-x}={1 \over e^{x}}}
，和所有的实数
x
{\displaystyle x}
![b^{{\frac {m}{n}}}={\sqrt[ {n}]{b^{m}}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b6ed2731781cb0d0d02467b366f6939c9e7592)
![{\sqrt[ {n}]{x}}=x^{{\frac {1}{n}}}=e^{{{\frac {\ln x}{n}}}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/291bce0c414e382cbcaaaafce18d5a3726d12099)
导数和微分方程[编辑]
，繪製紅色切線，和高度為
h
{\displaystyle h}
的垂直豎線，與在
x
{\displaystyle x}
![{\displaystyle {\begin{aligned}{\frac {d}{dx}}e^{x}&={\frac {d}{dx}}\left(1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}\right)=\sum _{n=1}^{\infty }{\frac {nx^{n-1}}{n!}}=\sum _{n=1}^{\infty }{\frac {x^{n-1}}{(n-1)!}}\\[6pt]&=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}},{\text{ where }}k=n-1\\[6pt]&=e^{x}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86128e9f129e565851026aed221433047fea96c7)
的形如
K
e
x
{\displaystyle Ke^{x}}
的函数是唯一有这个性质的函数（这得出自皮卡-林德洛夫定理[13]）。其他等价说法有：
的解。
exp是泛函导数的不动点。
，我们可以通过链式法则找到：
.
e
x
{\displaystyle e^{x}}
的廣義連分數收斂更快速:[14]
:
:
在複平面上[编辑]
在
n
{\displaystyle n}
而
n
{\displaystyle n}
弧度的角度。
[prove 1]，它可以写为
和
b
{\displaystyle b}
e
0
=
1
{\displaystyle \!\,e^{0}=1}
d
d
z
e
z
=
e
z
{\displaystyle \!\,{d \over dz}e^{z}=e^{z}}
(
e
z
)
n
=
e
n
z
,
n
∈
Z
{\displaystyle \,(e^{z})^{n}=e^{nz},n\in \mathbb {Z} }
和
w
{\displaystyle w}
。
，我们可以接着定义更一般性的指数函数：
，而是
(
e
z
)
w
=
e
(
z
+
2
π
i
n
)
w
{\displaystyle (e^{z})^{w}=e^{(z+2\pi in)w}\,}
多值於整數n 之上。
e
0
=
1
{\displaystyle \ e^{0}=1}
e
x
{\displaystyle \ e^{x}}
与
e
−
x
{\displaystyle \ e^{-x}}
是互倒的
e
x
{\displaystyle \ e^{x}}
的导数是从
u
{\displaystyle \ u}
到
u
e
x
{\displaystyle \ ue^{x}}
的线性映射。
f
(
0
)
=
1
{\displaystyle \ f(0)=1}
f
′
(
t
)
=
A
f
(
t
)
{\displaystyle \ f'(t)=Af(t)}
在李代数上[编辑]
前者成為定義因其有導數上的重要性質。
^ Ernest William Hobson, John Napier and the invention of logarithms, 1614, Cambridge: The University Press, 1914
^ Boyer, Carl B., 14, section "Jobst Bürgi", A History of Mathematics, New York: John Wiley & Sons, 1991, ISBN 978-0-471-54397-8
^
(
1
+
1
n
)
x
=
(
(
1
+
1
n
)
n
)
x
n
{\displaystyle \left(1+{\frac {1}{n}}\right)^{x}=\left(\left(1+{\frac {1}{n}}\right)^{n}\right)^{\frac {x}{n}}}
在最初的概念下，底數是接近1的數，而對數是整數；經過簡單變換後，底數變大了，成為接近數學常量e的數，而對數變小了，成為 x/n。
^ 選取接近e的底數b，對數表涉及的bx為單調增函數，定義域為0到1而值域為1到b；選取接近1/e的底數b，對數表涉及的bx為單調減函數，定義域為0到∞而值域為1到0。
^ 以
10
1
2
54
{\displaystyle 10^{\frac {1}{2^{54}}}}
這個接近1的數為基礎。
^ Kline, M. (1998) Calculus: An intuitive and physical approach, section 12.3 "The Derived Functions of Logarithmic Functions." （页面存档备份，存于互联网档案馆）, pp. 337 ff, Courier Dover Publications, 1998, ISBN 0-486-40453-6
^
lim
h
→
0
(
b
h
−
1
)
1
h
=
lim
1
n
→
0
(
b
1
n
−
1
)
n
=
lim
n
→
∞
n
(
b
1
/
n
−
1
)
=
ln
(
b
)
.
{\displaystyle {\begin{aligned}\lim _{h\to 0}\left(b^{h}-1\right){\frac {1}{h}}&=\lim _{{\frac {1}{n}}\to 0}\left(b^{\frac {1}{n}}-1\right)n\\&=\lim _{n\rightarrow \infty }n(b^{1/n}-1)\\&=\ln(b).\\\end{aligned}}}
這裡的自然對數定義為歐拉提出，是他定義的指數函數的逆函數。
^
d
d
x
(
1
+
x
n
)
n
=
n
n
+
x
(
1
+
x
n
)
n
.
{\displaystyle {\frac {d}{dx}}\left(1+{\frac {x}{n}}\right)^{n}={\frac {n}{n+x}}\left(1+{\frac {x}{n}}\right)^{n}.}
這個函數的導數與函數值的比為 n/(n+x)，當n→∞時， n/(n+x)=1，等式兩端就是指數函數的導數和指數函數。
^ 通过
y
(
t
)
=
e
t
,
y
(
0
)
=
K
{\displaystyle y(t)=e^{t},y(0)=K}
和
f
(
t
,
y
(
t
)
)
=
y
(
t
)
{\displaystyle f(t,y(t))=y(t)}
。
^ "A.2.2 The exponential function." L. Lorentzen and H. Waadeland, Continued Fractions, Atlantis Studies in Mathematics, page 268.. [2014-03-11]. （原始内容存档于2021-03-08）.
证明[编辑]
^
e
i
π
=
lim
n
→
∞
(
1
+
π
n
i
)
n
{\displaystyle e^{i\pi }=\lim _{n\rightarrow \infty }\left(1+{\frac {\pi }{n}}i\right)^{n}}
為
(
1
+
π
n
i
)
n
{\displaystyle \left(1+{\frac {\pi }{n}}i\right)^{n}}
的極限形式：
【本文地址】