【数学基础】 线性代数以及符号编总 |
您所在的位置:网站首页 › 括号表示什么 › 【数学基础】 线性代数以及符号编总 |
【数学基础】 线性代数以及符号编总
|
1基本概念和符号
线性代数可以对一组线性方程进行简洁地表示和运算。例如,对于这个方程组:
这里有两个方程和两个变量,如果你学过高中代数的话,你肯定知道,可以为x1 和x2找到一组唯一的解 (除非方程可以进一步简化,例如,如果第二个方程只是第一个方程的倍数形式。但是显然上面的例子不可简化,是有唯一解的)。在矩阵表达中,我们可以简洁的写作:
其中:
很快我们将会看到,咱们把方程表示成这种形式,在分析线性方程方面有很多优势(包括明显地节省空间)。 1.1基本符号 以下是我们要使用符号: 符号A ∈ Rm×n表示一个m行n列的矩阵,并且矩阵A中的所有元素都是实数。 符号x ∈ Rn表示一个含有n个元素的向量。通常,我们把n维向量看成是一个n行1列矩阵,即列向量。如果我们想表示一个行向量(1行n列矩阵),我们通常写作xT (xT表示x的转置,后面会解释它的定义)。 一个向量x的第i个元素表示为xi:
我们用aT i或 Ai,:表示矩阵的第i行元素:
矩阵 A ∈ Rm×n 和B ∈ Rn×p 的乘积为矩阵 :
其中:
请注意,矩阵A的列数应该与矩阵B的行数相等,这样才存在矩阵的乘积。有很多种方式可以帮助我们理解矩阵乘法,这里我们将通过一些例子开始学习。 2.1向量的乘积 给定两个向量x,y ∈ Rn,那么xT y的值,我们称之为向量的内积或点积。它是一个由下式得到的实数:
可以发现,内积实际上是矩阵乘法的一个特例。通常情况下xT y = yT x。 对于向量x ∈ Rm, y ∈ Rn(大小不必相同),xyT ∈ Rm×n称为向量的外积。外积是一个矩阵,其中中的每个元素,都可以由
我们举个例子说明外积有什么用。令1 ∈ Rn 表示所有元素都是1的n维向量,然后将矩阵 A ∈ Rm×n 的每一列都用列向量x ∈ Rm表示。使用外积,我们可以将A简洁的表示为:
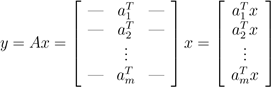
对于一个矩阵A ∈ Rm×n 和向量x ∈ Rn,他们的乘积为向量 y = Ax ∈ Rm。理解矩阵向量乘法的方式有很多种,我们一起来逐一看看。 以行的形式书写A,我们可以将其表示为Ax的形式:
也就是说,y第i行的元素等于A的第i行与x的内积 咱们换个角度,以列的形式表示A,我们可以看到:
换言之,y是A列的线性组合,线性组合的系数就是x的元素。 上面我们看到的是右乘一个列向量,那左乘一个行向量嘞?对于A ∈ Rm×n,x ∈ Rm, y ∈ Rn,这个式子可以写成yT = xT A 。向之前那样,我们有两种方式表达yT,这取决于表达A的方式是行还是列。第一种情况是把A以列的形式表示:
这个式子说明yT 第i列的元素等于向量x与A的第i列的内积。 我们也一样可以把A表示成行的形式,来说明向量-矩阵乘积。
我们可以看到yT 是A的行的线性组合,线性组合的系数是x的元素。 2.3矩阵-矩阵乘积基于以上知识,我们可以看到如之前所定义的矩阵-矩阵乘法C=AB有四种不同(但是等价)的理解方法。 首先,我们可以将矩阵-矩阵相乘看作一组向量-向量乘积。根据其概念,我们最好理解的方式是矩阵C的(i,j)元素是A的i行与B的 j列的内积。符号表达如下:
注意由于A ∈ Rm×n , B ∈ Rn×p, ai ∈ Rn bj ∈ Rn, 所以内积永远有意义。对矩阵乘法而言,以A的行和B的列表示是最"自然"的表示方法。当然,我们也可以以A的列和B的行的形式进行表示。表达方法是AB外积累加的形式,稍微复杂一点点。符号表达为:
换一种方式表达,AB的值等于对于所有的i,A的i列与B的i行的外积的和。因此,对于ai ∈ Rm 和 bi ∈ Rp,外积aibiT的维度是m×p,它与C的维度是相同的。等式可能有点难理解,花点时间想想,我猜你肯定能明白。 第二种理解方式是,我们也可将向量-向量乘法看做一系列的矩阵-向量乘积。具体来说,如果我们将B以列的形式表示,我们可以将C的每一列看做A和B列的矩阵-向量乘积。符号表达为:
可以将C的i列以矩阵-向量乘积(向量在右)的方式表示为ci = Abi. 这些矩阵-向量乘积可以用前面的两种观点解释。最后类比一下,我们以A的行形式表示,将C的行视为A的行与C的矩阵-向量乘积,符号表达为
在此,我们以矩阵-向量乘积(向量左乘)的形式表示了C的i列, 只是一个矩阵乘法而已,这么细的分析看上去好像没有必要,尤其是当我们知道矩阵乘法定义后其实很容易可以计算得到结果。然而,几乎所有的线性代数内容都在处理某种类型的矩阵乘法,因此花一些时间去形成对这些结论的直观认识还是很有帮助的。 此外,知道一些更高层次的矩阵乘法的基本性质也是有好处的: 结合律即(AB)C = A(BC) 分配率即A(B + C) = AB + AC 注意哦,矩阵乘法没有交换律,即AB ≠BA.(例如,如果A ∈ Rm×n 和B ∈ Rn×q,矩阵的乘积BA在m和q不等时,BA可能根本就不存在)如果你对这些性质不熟悉,最好花些时间自己证明一下。例如,为了验证矩阵乘法的结合律,对于A ∈ Rm×n, |
【本文地址】
今日新闻 |
推荐新闻 |
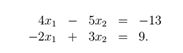
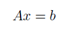
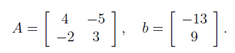


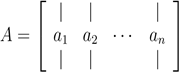
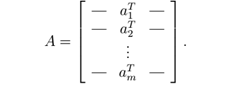
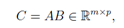
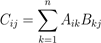 .
.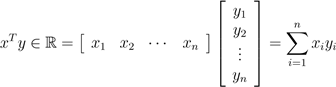 .
.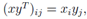 得到,也就是说,
得到,也就是说,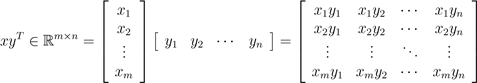 .
. .
. .
. .
.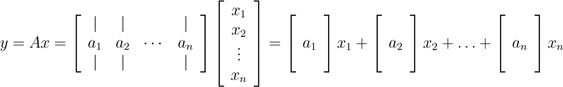 .
.

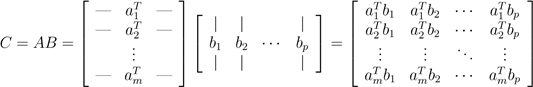 .
.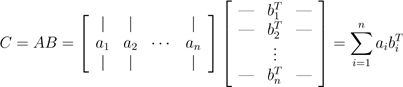 .
.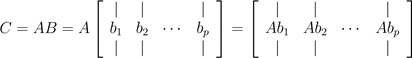 .
.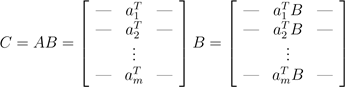 .
.