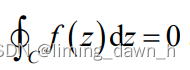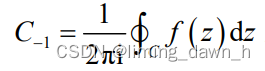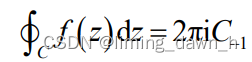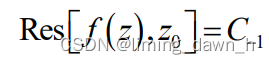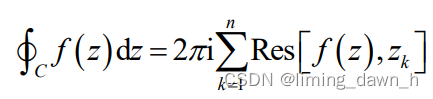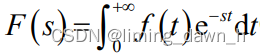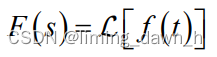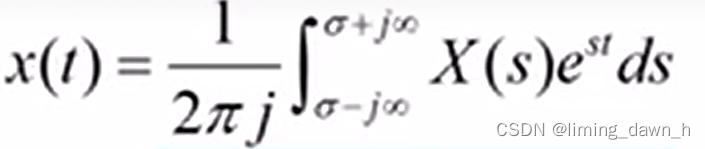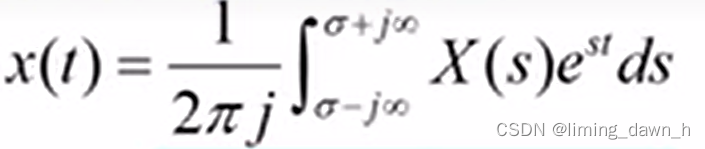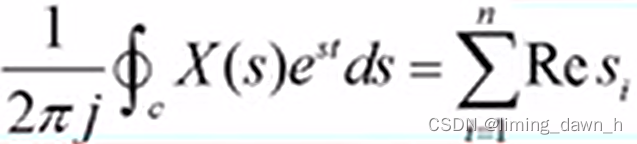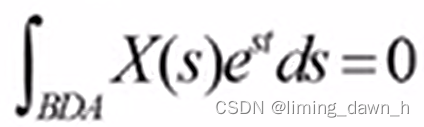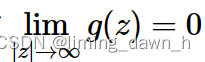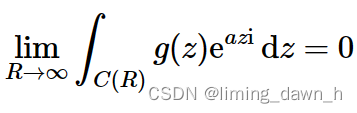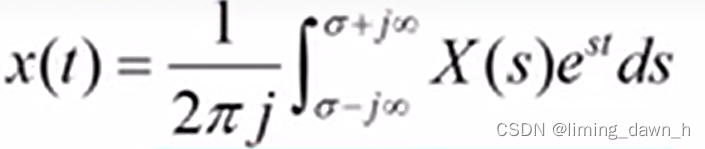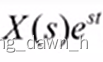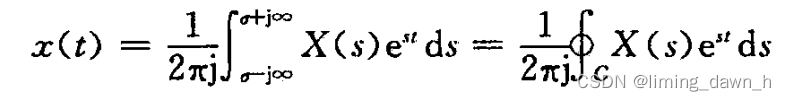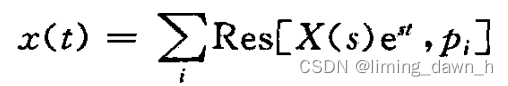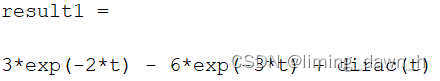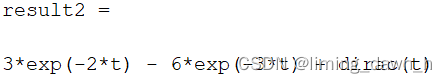一、理论分析

1、留数定理

当 f (z) 在简单闭曲线 C 上及其内部解析时，由柯西积分定理知

若上述 C 的内部存在函数 f (z) 的孤立奇点，由洛朗展开式知，取洛朗系数中n = -1 可得

即

再令

推广后得留数定理

2、拉普拉斯变换

拉普拉斯变换的意义在于它是一种数学工具，可以将复杂的微分方程、积分方程等转换为更易于处理和研究的代数方程。这使得我们在解决实际问题时，可以简化计算过程，更好地理解问题的本质。它是一种双边变换，将函数从一个域（如时域）转换到另一个域（如频域）。在变换过程中，函数的频率特性得以凸显，从而方便我们分析问题的动态行为。

设函数 f (t) 当t>=0时有定义，若积分

某一邻域内收敛，则称 F (s) 为函数 f (t) 的拉普拉斯变换，简称拉氏变换，记为

其逆变换记为

具体表示为

3、利用留数定理解决拉普拉斯逆变换问题

已知拉普拉斯逆变换

又根据留数定理有

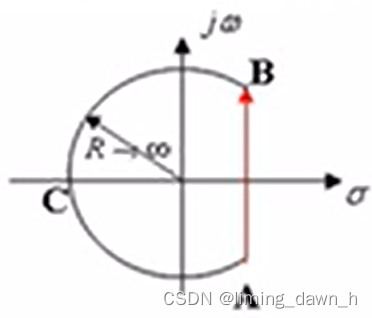
考虑添加辅助线，使拉普拉斯逆变换可以用留数定理表达

如图1

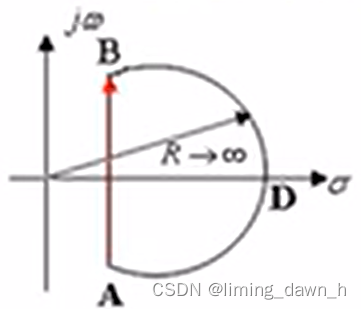
图2

其中图1要求

图2要求

根据Jordan引理

若g（z）连续，且满足

则那么对于任何正实数 a就有

其中C（R）是半径为 R 的半圆弧路径，圆心为原点，坐落于复平面上半平面，路径方向顺逆时针都一样。

根据约旦引理，配合辅助线可得

等于围线

所有极点的留数之和

最终得到下式

即

在用上式求x(t)时需注意:当x(t)中包含有冲激函数或其导数时，需先将X(S)分解为多项式与真分式之和，由多项式决定冲激函数及其导数项，再对真分式求留数决定其余各项。即X(S)需要是真分式。

二、matlab仿真

仿真阶段，我们假设所有输入的信号是右边信号，以F(s)=(s^2+2s+3)/(s^2+5s+6)为例，其中 F(s)的极点都是单极点

如下图所示

结果如下

直接调用matlab函数库ilaplace()函数，验证结果是否正确

结果如下

对比可知，利用留数定理可以解决拉普拉斯逆变换的计算问题。

三、总结

拉普拉斯变换在数学、物理、工程等领域具有广泛的应用。通过使用拉普拉斯变换，我们可以将复杂的微分方程转化为更简单的代数方程，进而求解。这种变换在求解偏微分方程、分析线性时不变系统、研究波动方程等方面具有重要意义。总之，拉普拉斯变换的意义在于它为科学家和工程师提供了一种有效的数学工具，使得他们在研究复杂问题时，可以简化计算过程，更好地理解问题的本质。这使得拉普拉斯变换在多个领域具有重要的理论和实际应用价值。

利用留数定理，可以很好的解决拉普拉斯逆变换的计算问题，有效简化运算，帮助理解拉普拉斯逆变换的过程。