|
**
所用的MATLAB函数:
**
dirac(t) 冲激函数 heaviside(t) 阶跃函数
laplace(ft) 单边拉普拉斯变换 ilaplace(Fs) 拉普拉斯逆变换
num=[1 0];den=[1 0 100]; %X=s/(s^2+100)
sys=tf(num,den); %建立一个传递函数,分子为num,分母为den
poles=roots(den) %求极点
pzmap(sys); %零极点分布图显示
[r,p,k]=residue(num,den)
num den分子分母多项式的系数向量
r部分分式的系数
p为极点
k为多项式系数,若为真分式,其为0
roots(den)函数计算H(s)的零极点
format rat %使用分数来表示数值
pretty(Ys);%看起来好看的Ys
yzit=vpa(yzit0,4); %vpa 设置精度,0.001111 四位
t1=linspace(eps,5,100); %eps = 1/4503599627370496=0+;
ht1=subs(ht,t,t1); %置换函数 syms t->t1数值点,求冲激函数各时点的数值解
t=0:0.02:15;mpulse(num,den,t);step(num,den,t); 冲激响应 阶跃响应绘图
[H,w]=freqs(num,den); plot(w,abs(H));plot(w,angle(H))求得幅频相频响应
正文
** ** 1.从傅里叶变换到拉普拉斯变换  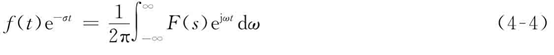 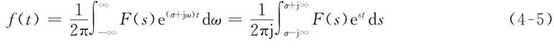 2.双边拉普拉斯变换的收敛域 2.双边拉普拉斯变换的收敛域 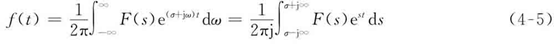 (1) 因果的。当t<0时,f(t)=0。若因果信号的双边拉普拉斯变换存在,则其收敛域在其极点右边的一个平面。 (2) 反因果的。当t>0时,f(t)=0。若反因果信号的双边拉普拉斯变换存在,则其收敛域在其极点左边的一个平面。 (3)非因果的,以上二者的组合。若非因果信号的双边拉普拉斯变换在,则其收敛域是其因果部分的收敛域和其反因果部分的收敛域的交集。 (1) 因果的。当t<0时,f(t)=0。若因果信号的双边拉普拉斯变换存在,则其收敛域在其极点右边的一个平面。 (2) 反因果的。当t>0时,f(t)=0。若反因果信号的双边拉普拉斯变换存在,则其收敛域在其极点左边的一个平面。 (3)非因果的,以上二者的组合。若非因果信号的双边拉普拉斯变换在,则其收敛域是其因果部分的收敛域和其反因果部分的收敛域的交集。
3.单边拉普拉斯变换 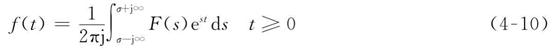  利用MATLAB求解laplace求信号的单边拉普拉斯变换 符号法: 利用MATLAB求解laplace求信号的单边拉普拉斯变换 符号法:
syms t s;
d=dirac(t);
D=laplace(d)
u=heaviside(t);
U=laplace(u)
g=heaviside(t+1)-heaviside(t-1);
G=laplace(g)
x=exp(-2*t);
X=laplace(x)
结果: D =1 U = 1/s G =1/s - exp(-s)/s X =1/(s + 2)
3.单边拉普拉斯变换的性质  MATLAB比较cos10t ε(t)和e–tcos10t ε(t)的极点位置,分析s域平移性质对收敛域的影响 符号计算法 MATLAB比较cos10t ε(t)和e–tcos10t ε(t)的极点位置,分析s域平移性质对收敛域的影响 符号计算法
clear
syms t s;
x=cos(10*t);
y=exp(-t)*cos(10*t);
X=laplace(x) %好像laplace函数就是求单边普,不用x=cos(10*t)*heaviside(t)了
Y=laplace(y) % plotting of signals and poles/zeros??
figure(1)
subplot(221)
ezplot(x,[0,5]);grid
axis([0 5 -1.1 1.1]);
title('x(t)=cos(10t)ε(t)')
num=[1 0];den=[1 0 100]; %X=s/(s^2+100)可知
sys=tf(num,den); %建立一个传递函数,分子为num,分母为den
poles=roots(den) %求极点
subplot(222)
pzmap(sys); %零极点分布图显示
axis([-2 1 -20 20]);
subplot(223)
ezplot(y,[-1,5]);grid
axis([0 5 -1.1 1.1]);
title('y(t)=cos(10t)exp(-t)ε(t)')
num=[0 1 1];den=[1 2 101];
sys=tf(num,den);
poles=roots(den)
subplot(224)
pzmap(sys);
axis([-2 1 -20 20]);
X = s/(s^2 + 100) Y = (s + 1)/((s + 1)^2 + 100) poles = 0.0000 +10.0000i 0.0000 -10.0000i poles = -1.0000 +10.0000i -1.0000 -10.0000i  4.单边拉普拉斯逆变换 4.1 部分分式展开法 1.单极点 实数 2.共轭复极点 4.单边拉普拉斯逆变换 4.1 部分分式展开法 1.单极点 实数 2.共轭复极点
format rat %使用分数来表示数值
num=[3 11 15 6];
den=[1,3,2];
[r,p,k]=residue(num,den)
r =
4
-1
p =
-2
-1
k =
3 2
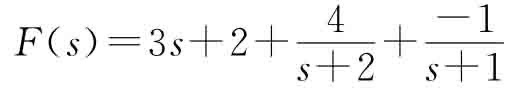
%F(s)=s^2-4/(s^2+4s+8)(s+3)
num=[1 0 -4];
den=conv([1 4 8],[1 3]); %卷积求多项式乘
[r,p,k]=residue(num,den)
magr=abs(r) %求r得模
angr=angle(r) %求r得相∩
```r=1+0i,1/321685687669322+1i,1/321685687669322-1i
p=-3+0i,-2+2i,-2-2i
magr=1,1,1
angr=0,355/226,-355/226
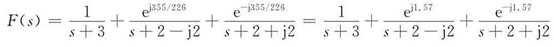 5 连续系统的拉普拉斯分析 5 连续系统的拉普拉斯分析  完全响应=零输入响应+零状态响应 完全响应=零输入响应+零状态响应
已知线性时不变系统的微分方程为 y″(t)+3y′(t)+2y(t)=f′(t)+3f(t) 输入信号f(t)=e–4tε(t),y(0–)=1,y′(0–)=1,求系统的零输入响应、零状态响应和全响应。
%y''+3y'+2y=f'+3f
syms t s;
ft=exp(-4*t)*heaviside(t); %输入信号
a=[1 3 2];b=[1 3];%微分方程系数向量
y0=[1 1]; %系统初始状态 y0(1)=y(0-) y0(2)=y'(0-)
Fs=laplace(ft);
%%计算Cs即C(s)
n=length(a)-1;Cs=0;
for k=1:n;
for r=0:(k-1);
Cs=Cs+a(n-k+1)*y0(r+1)*s^(k-1-r);
end
end
As=s^2+3*s+2;Bs=s+3;
Hs=Bs./As;
ht=ilaplace(Hs);disp('系统冲激响应');ht
Ys=Cs/As+Bs/As*Fs;disp('Y(s)=');
pretty(Ys);%看起来好看的Ys
yt=ilaplace(Ys);disp('全响应');yt
yzit0=ilaplace(Cs/As);yzit=vpa(yzit0,4); %vpa 设置精度,0.001111 四位
disp('零输入响应');yzit
disp('零输入响应');yzit
yzst0=ilaplace(Bs/As*Fs);yzst=vpa(yzst0,4);
disp('零状态响应');yzst
%%绘图
t1=linspace(eps,5,100); %eps = 1/4503599627370496=0+;
ht1=subs(ht,t,t1); %置换函数 syms t->t1数值点,求冲激函数各时点的数值解
subplot(211);plot(t1,ht1);
title('冲激响应');grid;
yt1=subs(yt,t,t1);subplot(212);plot(t1,yt1,'r--');
yzit1=subs(yzit,t,t1);hold on;plot(t1,yzit1,'k--');
yzst1=subs(yzst,t,t1);hold on;plot(t1,yzst1,'b--');
title('系统响应')
legend('全响应','零输入','零状态');
系统冲激响应
ht =
2*exp(-t) - exp(-2*t)
Y(s)=
s + 4 s + 3
------------ + ----------------------
s ^2 + 3 s + 2 (s + 4) (s^2 + 3 s + 2)
全响应
yt =
(11*exp(-t))/3 - (5*exp(-2*t))/2 - exp(-4*t)/6
零输入响应
yzit =
3.0*exp(-1.0*t) - 2.0*exp(-2.0*t)
零状态响应
yzst =
0.6667*exp(-1.0*t) - 0.5*exp(-2.0*t) - 0.1667*exp(-4.0*t)

已知线性时不变系统的系统函数H(s)=s+2/s^2+4
,输入信号f(t)=ε(t),求系统的零状态响应。
syms t s;
ft=heaviside(t);
Fs=laplace(ft);
As=s^2+4;Bs=s+2;Hs=Bs./As;
ht=ilaplace(Hs);
yzst0=ilaplace((Bs*Fs)/As);yzst=vpa(yzst0,4);
disp('零状态响应'),yzst,
t1=linspace(eps,5,100);
ht1=subs(ht,t,t1);
subplot(2,1,1);plot(t1,ht1),
xlabel('时间(秒)'),ylabel('幅度') ,grid,title('冲激响应'),
subplot(2,1,2);
yzst1=subs(yzst,t,t1);hold on;plot(t1,yzst1,'b-.')
xlabel('时间(秒)'),ylabel('幅度') ,grid,title('零状态响应')
6.系统函数与系统特性 (1)若极点位于s平面的坐标原点,即Hs=1/s,则h(t)=ε(t),冲激响应是阶跃信号。 (2)若极点位于s平面的实轴上,即Hs=1/s+a,则h(t)=e–atε(t),若a>0,冲激响应是指数衰减信号;若a<0,冲激响应是指数增长信号。 (3)若极点位于s平面的虚轴上,即Hs=w0/s2+w02,则h(t)=sinω0t ε(t),冲激响应是等幅的正弦振荡。 (4)若极点位于s平面的左半平面,并共轭成对,即Hs=w0/(s+a)2+w02,则h(t)=e–atsinω0t ε(t),此时a>0,冲激响应是衰减振荡;若a<0,极点位于s平面的右半平面,则冲激响应是增幅振荡。 若系统函数具有重极点,那么重极点对应的部分分式的逆变换可能具有t,t2,…与指数函数相乘的形式 
%求零极点分布图,冲激响应h(t)和阶跃响应g(t)
%先定义系统函数的分子分母系数向量,然后求零极点,最后用impulse step函数画出波形
num=[1 -2];den=[1 1 0];
sys=tf(num,den);
%%求极点
poles=roots(den)
figure(1)
subplot(231)
pzmap(sys);
%%求响应画图
t=0:0.02:15;
subplot(232);impulse(num,den,t);
subplot(233);step(num,den,t);
%第二个
num=[2 2];den=conv([1 0 1 0],[1 0 1])
sys=tf(num,den);
poles=roots(den)
subplot(234);pzmap(sys);
t=0:0.02:15;
subplot(235);impulse(num,den,t);
subplot(236);step(num,den,t);
%%另一种方法求冲击阶跃响应的表达式并画图
figure(2)
clear
syms t s;
ft=dirac(t)
Fs=laplace(ft)
Bs=s-2;As=s^2+s;
Hs=Bs./As; %Ys(全响应)=Cs/As(零输入)+Hs*Fs(零状态) 然后用ilaplace求t 冲激响应Fs=1 阶跃响应1/s
ht=ilaplace(Hs*Fs) %表达式冲激函数
t1=linspace(eps,5,100);
ht1=subs(ht,t,t1);
subplot(211)
plot(t1,ht1);
ft=heaviside(t);
Fs=laplace(ft);
Bs=s-2;As=s^2+s;Hs=Bs./As;
ht=ilaplace(Hs*Fs) %表达式冲激函数
t1=linspace(eps,5,100);
ht1=subs(ht,t,t1);
subplot(212)
plot(t1,ht1);
  零极点分布决定系统的频率特性 零极点分布决定系统的频率特性
%Hs=s-1/(s+1)^2+4 求系统幅频和相频 用freqs函数产生幅频相频特效
num=[1 -1];den=[1 2 5];
sys=tf(num,den);
poles=roots(den)
subplot(2,2,1);pzmap(sys);
axis([-1.5 1.5 -3 3]);
t=0:0.02:10;
h=impulse(num,den,t);
subplot(2,2,2);plot(t,h);
title('Impulse Response')
[H,w]=freqs(num,den);
subplot(2,2,3);plot(w,abs(H))
xlabel('\omega');
title('M agnitude Response')
subplot(2,2,4);plot(w,angle(H))
xlabel('\omega');
title('Phase Response')

系统的稳定性 实际应用中,通常利用H(s)的极点分布来判断系统的稳定性。根据极点的分布状况,系统可分为稳定的、临界稳定的和不稳定的。 (1)稳定系统:若H(s)的极点全部位于s平面的左半平面,则系统是稳定的。 (2)临界稳定系统:若H(s)在原点或虚轴上有单阶极点,其余的极点全部位于s平面的左半平面,则系统是临界稳定的。 (3)不稳定系统:若H(s)的极点不全位于s平面的左半平面,或在原点或虚轴上有高阶重极点,则系统是不稳定的。
|

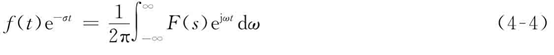
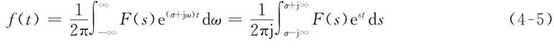 2.双边拉普拉斯变换的收敛域
2.双边拉普拉斯变换的收敛域 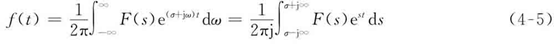 (1) 因果的。当t<0时,f(t)=0。若因果信号的双边拉普拉斯变换存在,则其收敛域在其极点右边的一个平面。 (2) 反因果的。当t>0时,f(t)=0。若反因果信号的双边拉普拉斯变换存在,则其收敛域在其极点左边的一个平面。 (3)非因果的,以上二者的组合。若非因果信号的双边拉普拉斯变换在,则其收敛域是其因果部分的收敛域和其反因果部分的收敛域的交集。
(1) 因果的。当t<0时,f(t)=0。若因果信号的双边拉普拉斯变换存在,则其收敛域在其极点右边的一个平面。 (2) 反因果的。当t>0时,f(t)=0。若反因果信号的双边拉普拉斯变换存在,则其收敛域在其极点左边的一个平面。 (3)非因果的,以上二者的组合。若非因果信号的双边拉普拉斯变换在,则其收敛域是其因果部分的收敛域和其反因果部分的收敛域的交集。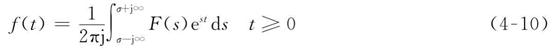
 利用MATLAB求解laplace求信号的单边拉普拉斯变换 符号法:
利用MATLAB求解laplace求信号的单边拉普拉斯变换 符号法: MATLAB比较cos10t ε(t)和e–tcos10t ε(t)的极点位置,分析s域平移性质对收敛域的影响 符号计算法
MATLAB比较cos10t ε(t)和e–tcos10t ε(t)的极点位置,分析s域平移性质对收敛域的影响 符号计算法 4.单边拉普拉斯逆变换 4.1 部分分式展开法 1.单极点 实数 2.共轭复极点
4.单边拉普拉斯逆变换 4.1 部分分式展开法 1.单极点 实数 2.共轭复极点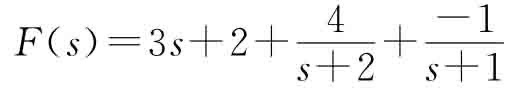
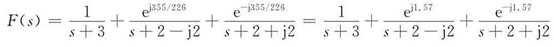 5 连续系统的拉普拉斯分析
5 连续系统的拉普拉斯分析  完全响应=零输入响应+零状态响应
完全响应=零输入响应+零状态响应


 零极点分布决定系统的频率特性
零极点分布决定系统的频率特性