数字信号处理 |
您所在的位置:网站首页 › 抽样频谱 › 数字信号处理 |
数字信号处理
|
目录 数字信号处理——信号频谱分析-N点DFT 频谱分析 频谱 频谱分析 离散傅里叶变换 Matlab 代码: 结论: 离散傅里叶变换的应用之一:用FFT分析信号频谱 解题关键: 1、分清"截取数据长度"(即窗函数长度)与"DFT点数"二者的不同; 2、能够根据模拟频率推断出DFT谱峰处对应的序号k的数值, 方法如下: 数字信号处理——信号频谱分析-N点DFT 频谱分析频谱分析是一种将复杂信号分解为较简单信号的技术。许多物理信号均可以表示为许多不同频率简单信号的和。找出一个信号在不同频率下的信息(如振幅、功率、强度或相位等)的做法即为频谱分析。 频谱频谱是指一个时域的信号在频域下的表示方式,可以针对信号进行傅里叶变换而得,所得的结果会是以分别以幅度及相位为纵轴,频率为横轴的两张图,不过有时也会省略相位的信息,只有不同频率下对应幅度的资料。有时也以“幅度频谱”表示幅度随频率变化的情形,“相位频谱”表示相位随频率变化的情形。 简单来说,频谱可以表示一个信号是由哪些频率的弦波所组成,也可以看出各频率弦波的大小及相位等信息。 信号若随着时间变化,且可以用幅度来表示,都有其对应的频谱。包括可见光(颜色)、音乐、无线电波、振动等都有这様的性质。当这些物理现象用频谱表示时,可以提供一些此信号产生原因的相关信息。例如针对一个仪器的振动,可以借由其振动信号频谱的频率成分,推测振动是由哪些元件所造成。 频谱分析频谱分析是一种将复杂信号分解为较简单信号的技术。许多物理信号均可以表示为许多不同频率简单信号的和。找出一个信号在不同频率下的信息(可能是幅度、功率、强度或相位等)的作法就是频谱分析。 频谱分析可以对整个信号进行。不过有时也会将信号分割成几段,再针对各段的信号进行频谱分析。周期函数(例如:sin(t))最适合只考虑一个周期的信号来进行频谱分析。傅里叶分析中有许多分析非周期函数时需要的数学工具。 一个函数的傅里叶变换包括了原始信号中的所有信息,只是表示的型式不同。因此可以用反傅里叶变换重组原始的信号。若要完整的重组原始信号,需要有每个频率下的幅度及其相位,这些信息可以用二维向量、复数、或是极座标下的大小及角度来表示。在信号处理中常常考虑幅度的平方,也就是功率,所得的就是功率谱密度。 实际上,大部分的仪器及软件都用快速傅里叶变换来产生频谱的信号。快速傅里叶变换是一种针对采样信号计算离散傅里叶变换的数学工具,可以近似傅里叶变换的结果。 随机性信号(或噪声)的傅里叶变换也是随机性的。需要利用一些取平均值的方式来得到其频率分布(frequency distribution)。一般来说会将资料依一定的时间分段,将各段资料进行傅里叶变换,再将变换后的幅度或幅度平方(幅度平方较常用)平均,以得到傅里叶变换的平均值。在处理取様的时域资料时,常用上述的作法,配合离散傅里叶变换来处理,这种处理方式称为Welch法(Welch's method)。若所得的频谱是平的,此信号会视为“白噪声”,不过许多信号在时域下看似噪声,却可以借由这样的处理方式得到一些频域的信息。 离散傅里叶变换离散傅里叶变换(DFT)是傅里叶变换在时域和频域上都呈现离散的形式,将时域信号的采样变换为在频域的采样。在实际应用中通常采用快速傅里叶变换(FFT)以高效计算DFT。 DFT的定义为:
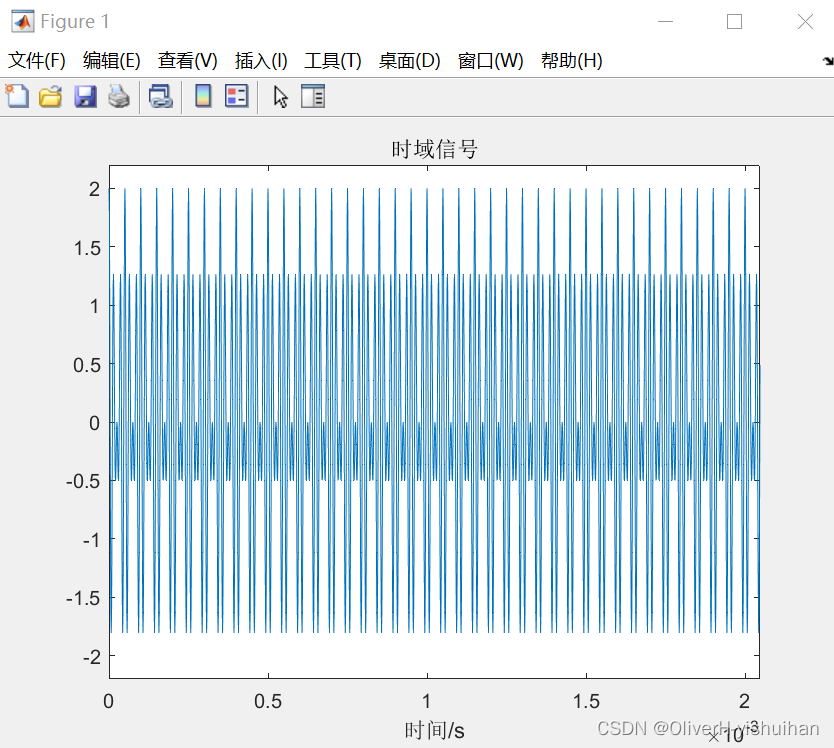
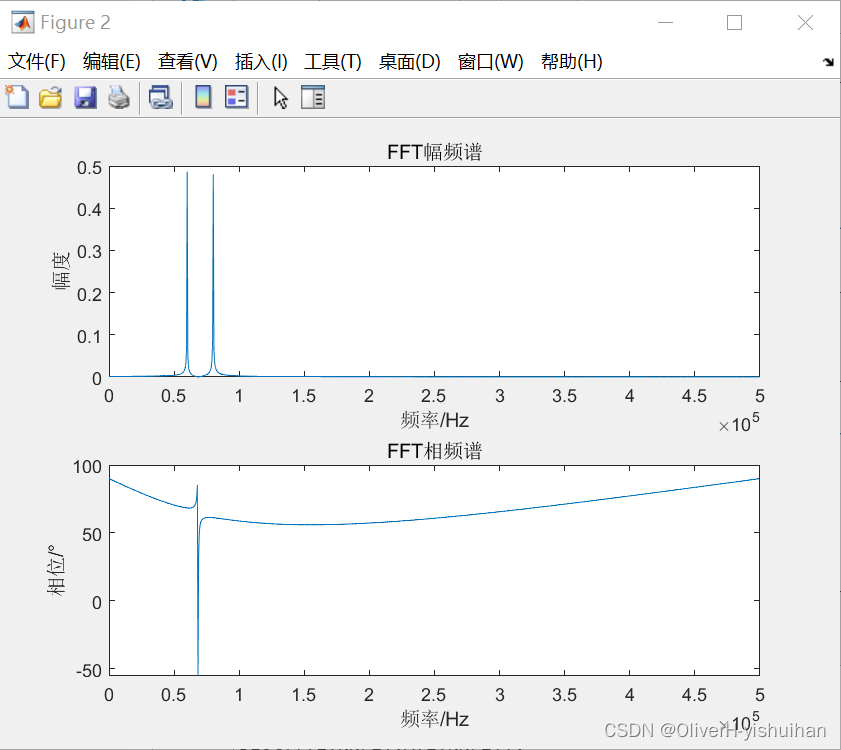
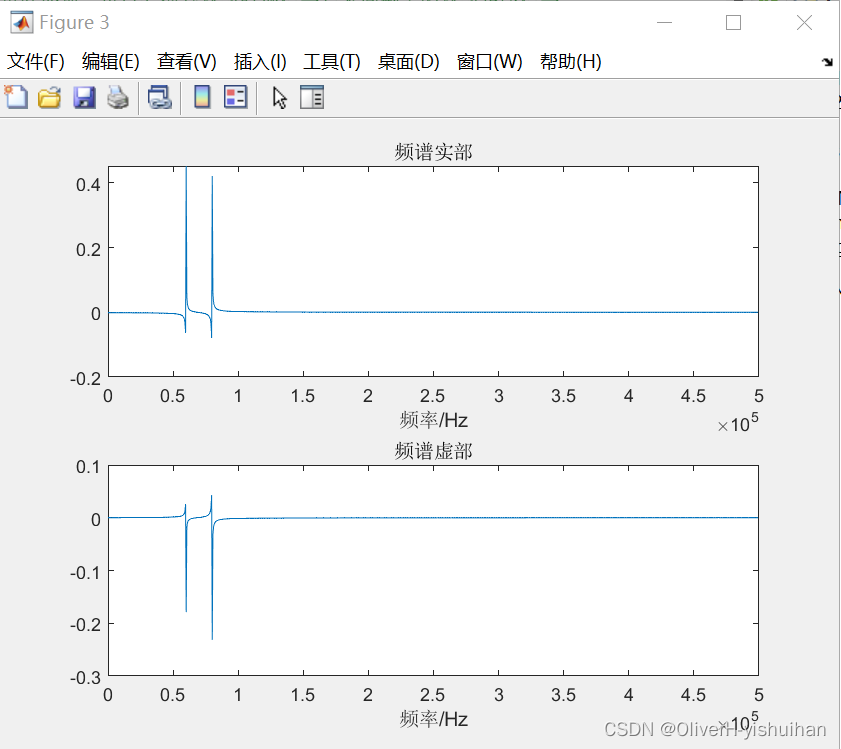
离散傅里叶变换可以看做是离散时域信号与不同频率的离散正弦信号进行相关运算得到相应的频率对应的幅值(复数)。 Matlab 代码: clc clear close all N = 2048;% ADC采样点数 Fs = 1e6;% ADC采样率 t = (0:N-1)/Fs;% 采样时间序列 F1 = 60e3;% 信号频率1 F2 = 80e3;% 信号频率2 signal = cos(2*pi*F1 * t) + cos(2*pi*F2 * t); figure; plot(t,signal); axis([0 inf -2.2 2.2]); xlabel('时间/s'); title('时域信号'); % FFT NN = 2048;% NN点DFT XN = fft(signal,NN)/NN;% 计算signal的NN点快速傅里叶变换 f0 = Fs/NN; % 频率分辨率 f = (0:NN-1)*f0; % 频率序列(模拟频率) fk = (0:NN-1); % 谱线序列 A = abs(XN); % 幅值序列 Phase = atan(-real(XN)./imag(XN))/pi*180; % 相位序列 figure; subplot(2,1,1); plot(f(1:NN/2),A(1:NN/2)); xlabel('频率/Hz');ylabel('幅度'); % axis([50e3 90e3 0 inf]); title('FFT幅频谱'); subplot(2,1,2); plot(f(1:NN/2),Phase(1:NN/2)); xlabel('频率/Hz');ylabel('相位/°'); title('FFT相频谱'); figure; subplot(2,1,1); plot(f(1:NN/2),real(XN(1:NN/2))); xlabel('频率/Hz'); title('频谱实部'); subplot(2,1,2); plot(f(1:NN/2),imag(XN(1:NN/2))); xlabel('频率/Hz'); title('频谱虚部');
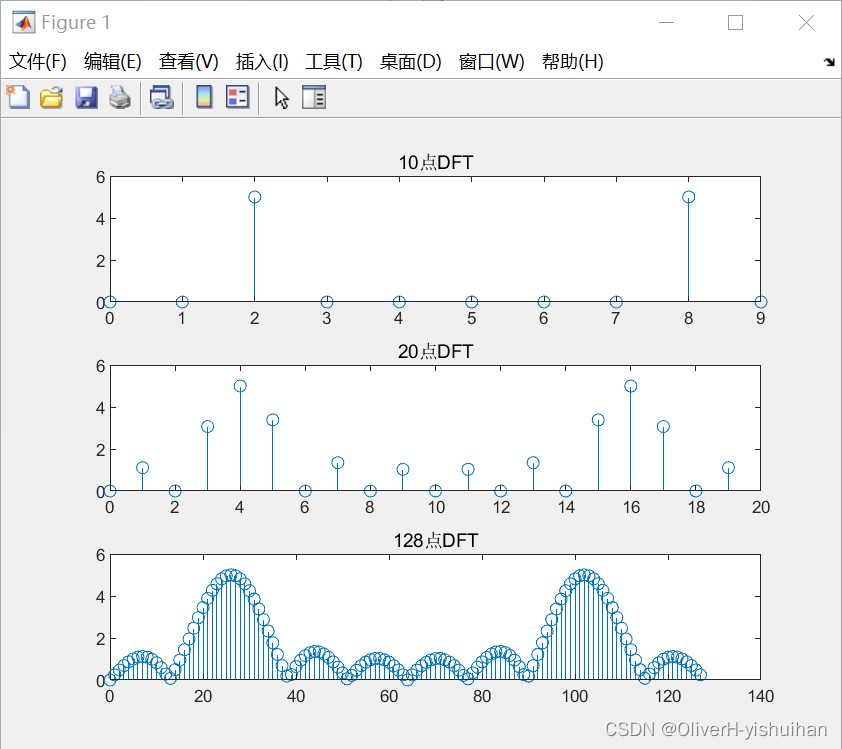
结论:对实信号做N点DFT,我们只需要看前N/2根谱线就行了,不用关注N/2~N-1之间的。 离散傅里叶变换的应用之一:用FFT分析信号频谱题目如下: 例:对模拟信号xa(t)=cos(2*pi*t)进行抽样,抽样频率为 fs=5Hz,加矩形窗截取10点长,做N点DFT得到X(k)的图形。 (1)N=10 (2)N=20 (3)N=128 解题关键: 1、分清"截取数据长度"(即窗函数长度)与"DFT点数"二者的不同; 2、能够根据模拟频率推断出DFT谱峰处对应的序号k的数值, 方法如下: 首先,由模拟频率转换为数字域频率:模拟频率 f (单位Hz)与数字域 w 的对应关系为:w=2*pi*f/fs,其中,fs (单位Hz)为采样频率。然后,数字域频率对应到DFT的序号k,数字域频率w 与DFT中的序号k的对应关系为:w=2*pi*k/N,其中,N为DFT点数。所以,模拟频率f(单位Hz)与DFT中的序号k的对应关系为:k=N*f/fs,其中,fs(单位Hz)为采样频率,N为DFT点数。模拟频率:f = k*fs/N,单位Hz。结论:对实信号做N点DFT,我们只需要看前N/2根谱线就行了,不用关注N/2~N-1之间的。 clc; clear; close all; f0 = 1; fs = 5;% 取样频率 fs=5Hz n = 0:1000; L = 10; xn = cos(2*pi*f0*n/fs);% 时域离散时间信号 xk1 = fft(xn(1:L), 10);% 返回 n 点 DFT。如果未指定任何值,则 Y 的大小与 X 相同。 xk2 = fft(xn(1:L), 20); xk3 = fft(xn(1:L), 128); xk4 = fft(xn(1:128), 128); subplot(311); stem((0:length(xk1)-1), abs(xk1)); title('10点DFT'); subplot(312); stem((0:length(xk2)-1), abs(xk2)); title('20点DFT'); subplot(313); stem((0:length(xk3)-1), abs(xk3)); title('128点DFT'); figure subplot(211); stem((0:length(xk4)-1), abs(xk4)); title('截取128点长,做128点DFT'); subplot(212); plot((0:length(xk4)/2-1)*fs/128, abs(xk4(1:length(xk4)/2))); title('截取128点长,做128点DFT'); xlabel('Hz'); ylabel('幅度');
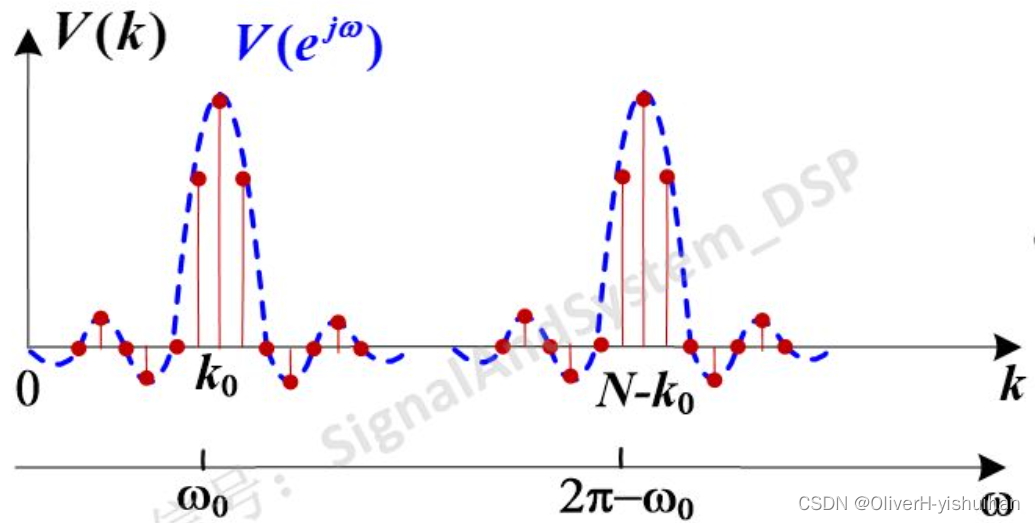
下面分析一下: 首先看N=10时,此时的结果看似最为干净清爽,只有干干净净两根线。但有的同学要问了,单频信号,只有一个频率成分,应该只有一根谱线呀?为什么会有两根? 我们先看第一根,k=2 那个谱线,对应频率为 f = 2*fs/10 = 2*5/10 = 1Hz,与题设 cos(2*pi*t) 完全吻合。k=8 那根谱线是怎么一回事呢?是负频率周期延拓过去的,本来在-2,-2+10就等于8了。所以,(敲黑板,以下结论很重要) 对实信号做N点DFT,我们只需要看前N/2根谱线就行了,不用关注N/2~N-1之间的。 再看 N=20 和 N=128 的DFT结果,怎么出来那么多根谱线呢? 回过头去看一看,做DFT之前的截取L点长的序列 cos(2*pi*n/5) 的频谱到底是什么样子呢?如下图中的虚线所示。
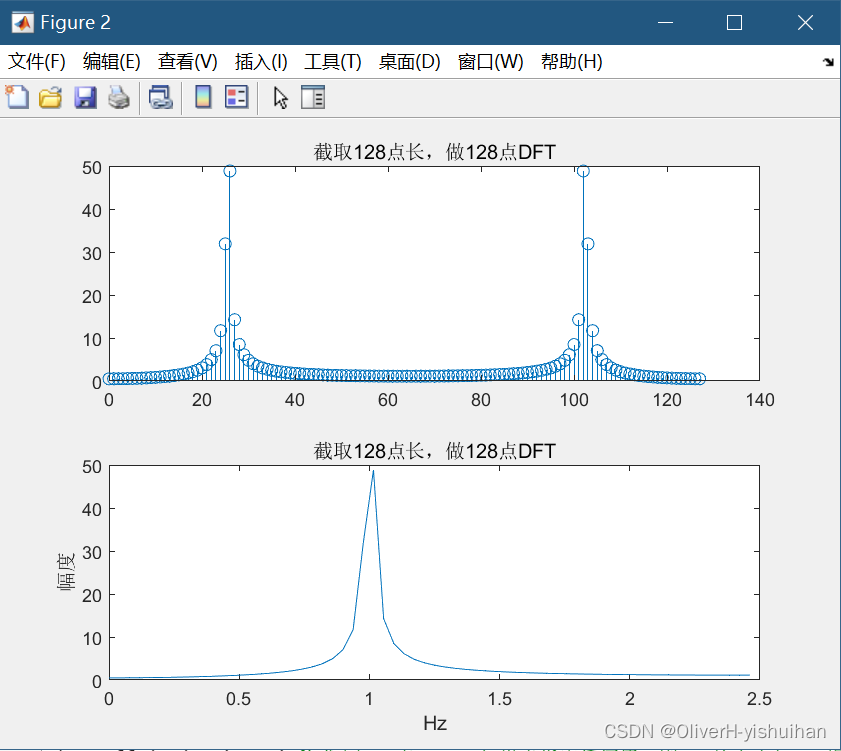
而 N 点DFT,是对V(e^jw)在 [0,2*pi] 区间抽取N个点。相当于把连续的频谱图(V(e^jw),用一张不透明的纸盖住,纸上以 2*pi/N 为间隔开了一些缝,露出来的点才是我们得到的DFT的结果。这就是频域抽样产生的“栅栏效应”。 所以,不管是10点DFT干干净净的两根线,还是128点DFT密密麻麻的那么多根线,背后隐藏的,都是连续的频谱函数。之所以10点DFT的结果看起来更顺眼,无非是因为 2*pi/N 也恰好是旁瓣的宽度(因为信号的周期和截取长度也是10) 在DFT谱分析中,当DFT 点数 N 大于数据本身的实际点数 L 时,相当于在数据后面补上了L-N个0再做DFT,称为"补零DFT"。补零经常是必要的,补零相当于对信号频谱以更小的间隔采样,得到更多的频谱的信息。而且有时数据长度不是2的整数次幂,如果我们想采用基2FFT算法,就必须进行补零。 是不是这样呢?当然了,如果你知道这个周期信号的周期是多少,毫无疑问,就截取一个周期的数据,做同样点数的DFT,结果最好看。但在分析实际问题时,要么信号根本没有周期性;要么虽然有周期性,但你不知道;而且实际信号也不会是简单的单频信号,会包含多个频率分量。这个时候,在系统性能、实时性、存储量等等容许的范围内,截取尽量长的数据(即获取更多的信息,得到更高的频率分辨率),做尽量多点数的DFT(即对频谱进行更为精细的采样)。 而且,实际应用中,由于DFT的点数一般都比较大,我们一般不会以离散的形式画频谱图,而是直接将频谱图化成连续的曲线。例如,上例中,我们截取128点长的数据,做128点DFT,用连续曲线形式画图(matlab中为plot函数),并且只画出前一半(即0~N/2-1)的点,并且把横轴直接转换为Hz,如下图所示:
上图中,横轴单位为:Hz。采用如下公式,将序号k转换为模拟频率Hz:
DFT分析信号频谱,是实际中应用最广泛的数字信号处理算法,还有很多种题目可以出。还是那句话,题目无穷无尽,而原理就那么多,大家只有掌握了其真正含义,才能以不变应万变。 |
【本文地址】
今日新闻 |
推荐新闻 |
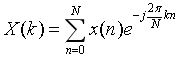 其中,N为DFT的点数,点数越大频率分辨率越高,k=0,1,2,…,N-1。
其中,N为DFT的点数,点数越大频率分辨率越高,k=0,1,2,…,N-1。