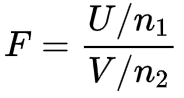【统计学】各统计量及其抽样分布(z分布,t分布,卡方分布) |
您所在的位置:网站首页 › 抽样分布的四个定理 › 【统计学】各统计量及其抽样分布(z分布,t分布,卡方分布) |
【统计学】各统计量及其抽样分布(z分布,t分布,卡方分布)
|
1. 前言
数据分析行业不可避免会与统计学打交道。常见的分析总体的过程如图所示:
常见的假设检验中,AB测试是最为出名的假设检验的过程,而需要深刻理解假设检验,先验知识统计量及其抽样分布的理解至关重要,这会为我们学习假设检验打下坚实的基础,本文章便是关于统计量及其抽样分布的讲解。 2. 统计量建议专业讲解和大白话结合一起看,更易理解。 2.1 专业讲解设X1, X2, ..., Xn是从总体X中抽取的容量为n的一个样本,如果由此样本构造一个函数T(X1, X2, ..., Xn),不依赖于任何未知参数,则称函数T(X1, X2, ..., Xn)是一个统计量。 注: 统计量是一个随机变量当获得特定样本具体观察值x1, x2, ..., xn时,计算出T(x1, x2, ..., xn)的数值,就获得一个具体的统计量的值以上,X表示多种总体中的组合,x表示确定的观察值 2.2 大白话设X1, X2, ..., Xn是从总体X中抽取的容量为n的一个样本,比如要研究人群总体身高均值,抽样得到一组样本的n各不同身高。根据这些不同的身高,构造统计量T(x1, x2, ..., xn),表示计算这组样本的身高均值。 样本的身高均值便是我们得到的统计量,但是这个统计量是随机的,因为我们所抽取的样本是随机的n个不同身高。 2.3 常用统计量以下将给出7个统计量的计算公式,但通常我们使用最多的是前三个统计量。 2.3.1 样本均值
样本统计量的分布即抽样分布。 3.1.1 专业讲解 当我们要对某一总体的参数进行估计时,就要研究来自该总体的所有可能的样本统计量的分布问题。其结果来自容量相同的所有可能样本。抽样分布、参数估计和假设检验是统计推断的三个中心内容。 3.1.2 大白话 拿身高来举例,要估计总体人群身高均值,要研究来自总体的多组样本的身高均值的分布。每组样本的数量要一样。根据得到的分布,进行假设检验,有利于我们进行统计推断。 3.2设X ~ N( 令Y = 当总体X ~ N(
卡方分布的期望:n,其中,n为自由度 卡方分布的反差:2n,其中,n为自由度 3.2.2 可加性设U服从自由度为n1的卡方分布,V服从自由度为n2的卡方分布,则U+V服从自由度为n1+n2的卡方分布。 3.3 t分布 3.3.1 来源
其中,S为样本标准差,S/根号n为样本均值的标准误。 3.4 F分布 3.4.1 来源设U服从自由度为n1的卡方分布,V服从自由度为n2的卡方分布,则称F为服从自由度n1和n2的F分布,记为:
以统计量样本均值为例,中心极限定理的意思是,在大样本且有放回的抽样中,不论总体是什么分布,最终的样本均值服从均值为 其中多组样本的均值 样本均值的抽样分布与总体分布的关系如下图所示:
无放回抽样与有放回抽样的区别是,最终的样本均值服从均值为 其中,N为总体个数,n为每组样本个数。 (N-n) / (N-1)为修正系数 由此可见,在总体趋近无限的情况下,该修正系数可视为1,可以直接使用有放回抽样。 5. 样本比例的抽样分布 5.1 有放回抽样样本比例的抽样分布适用于样本容量较大的情况, 设总体比例为π,样本比例为p。样本期望E(p) = π,样本方差 根据中心极限定理:p ~ N(π,π(1-π) / n) 5.2 无放回抽样无放回抽样中,方差后同样加个修正系数,与之前的修正系数一样。 6. 样本均值之差和比例之差的抽样分布 6.1 两个正态总体两个总体都为正态分布,即 其分布的数学期望为两个总体均值之差 E( 方差为各自的方差之和 图示如下:
样本比例之差的抽样分布同样可以类推,在这就不详述了。 7. 样本方差的抽样分布 7.1 单样本方差对于来自正态总体的简单随机样本,则比值 两个总体都为正态分布,即X1, X2, ..., Xn是来自总体X ~ 说明: 由7.1可知, 同时由3.4可知,这两个卡方分布相除,会得到服从分子自由度为(n1-1),分母自由度为(n2-1)的F分布。 |
【本文地址】
今日新闻 |
推荐新闻 |








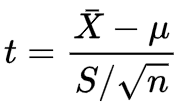 服从于自由度为n-1的t分布
服从于自由度为n-1的t分布