1.离心率：\(e=\dfrac{c}{a}\) ，其中圆的离心率 \(e=0\) ；椭圆的离心率 \(e\in(0,1)\) ；抛物线的离心率 \(e=1\) ；双曲线的离心率 \(e\in(1,+\infty)\)

2.准线：焦点在 \(x\) 轴上的椭圆、双曲线： \(x=\dfrac{a^2}{c}\) 或 \(x=-\dfrac{a^2}{c}\)

​ 焦点在 \(y\) 轴上的椭圆、双曲线： \(y=\dfrac{a^2}{c}\) 或 \(y=-\dfrac{a^2}{c}\)

​ 焦点在 \(x\) 轴上的抛物线：\(x=-\dfrac{p}{2}\)

​ 焦点在 \(y\)轴上的抛物线：\(y=-\dfrac{p}{2}\)

3.焦准距：\(p\) 即为焦点到准线的距离

4.通径长：椭圆、双曲线：\(\dfrac{2b^2}{a}\) 或 \(2ep\) ，其中 \(e\) 为椭圆的离心率，\(p\) 为椭圆的焦准距

​ 抛物线：\(2p\) ，其中 \(p\) 为抛物线的焦准距

5.半通径长：通径长的一半

核心内容：过一点 \(P\) 的两条直线与圆锥曲线交于 \(A,B\) 两点，如果直线 \(PA\) 和 \(PB\) 斜率乘积是定值，则直线 \(AB\) 过顶点，若 \(AB\) 过定点则 \(PA,PB\) 斜率乘积为定值

1.极点极线：下图给出圆中极点极线的三种情况，实际上极点极线对于任意圆锥曲线均适用。可以使用半代入方法快速求解极点极线。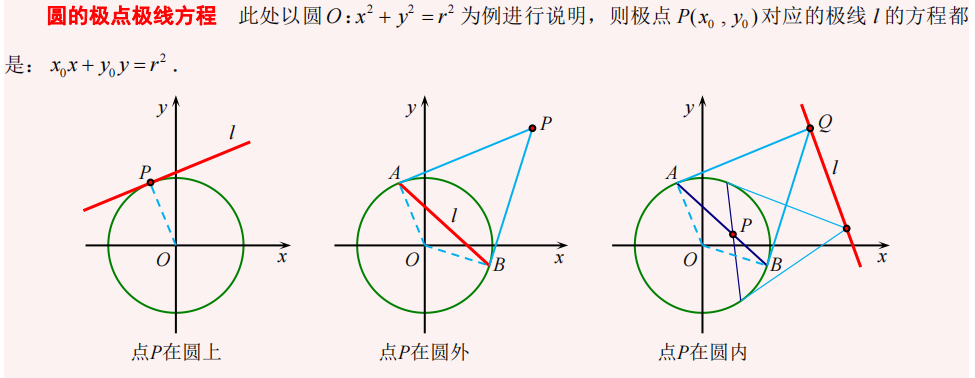

下面给出证明思路：对于极线是切线的情况可以先半代入写出直线方程，再联立证明 \(\delta=0\) ，而对于极线在圆锥曲线外或圆锥曲线内的情况则可以构造同构式，利用直线的同一性进行证明。

2.调和点列：若直线 \(l\) 上四个点 \(A,B,C,D\) ，满足 \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\) 则称 \(A,C；B,D\) 四个点是一组调和点列

3.调和共轭：若四个点 \(P,Q;A,B\) 四个点是一组调和点列，且 \(A,B\) 位于圆锥曲线上，则 \(P,Q\) 关于 \(C\) 调和共轭。

引申一个结论，设一点 \(P(x,y)\) 在圆锥曲线外，设 \(A,B\) 分别为点 \(P\) 处的极线与圆锥曲线的两个交点，则过点 \(P\) 任意做一条直线与圆锥曲线交于两点 \(C,D\) ，与线段 \(AB\) 交于一点 \(M\) 则 \(P,M;C,D\) 为一组调和点列。如下图所示。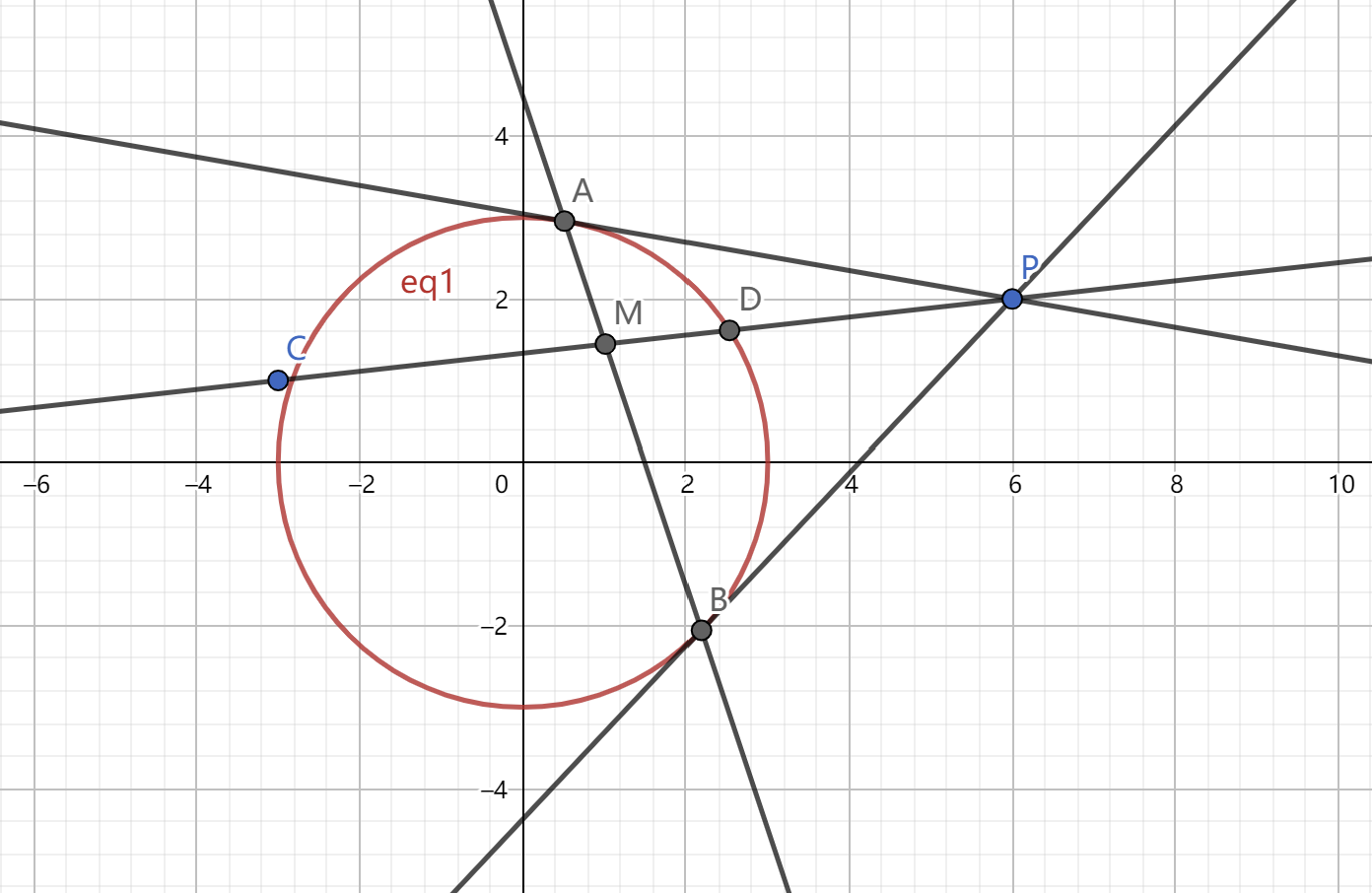

4.调和线束：四条直线 \(l_1,l_2,l_3,l_4\) 交于一点，计直线 \(l_i,l_j\) 的夹角为 \(\alpha_{ij}\)，若 \(\dfrac{\sin \alpha_{12}}{\sin \alpha_{23}}=\dfrac{\sin \alpha_{41}}{\sin \alpha_{34}}\) ，则 \(l_1,l_3;l_2,l_4\) 被称为调和线束。同时调和线束还有一个交比不变性，即对于一组调和线束，用任意一条直线去截这四条直线所得的四个点是一组调和点列。

1.椭圆：第三定义浅显理解，椭圆上一定点到椭圆左右顶点的斜率之积为定值 \(k_1 k_2=-\dfrac{b^2}{a^2}\)（焦点在 \(x\) 轴上） 或 \(k_1 k_2=-\dfrac{a^2}{b^2}\) （焦点在 \(y\) 轴上）。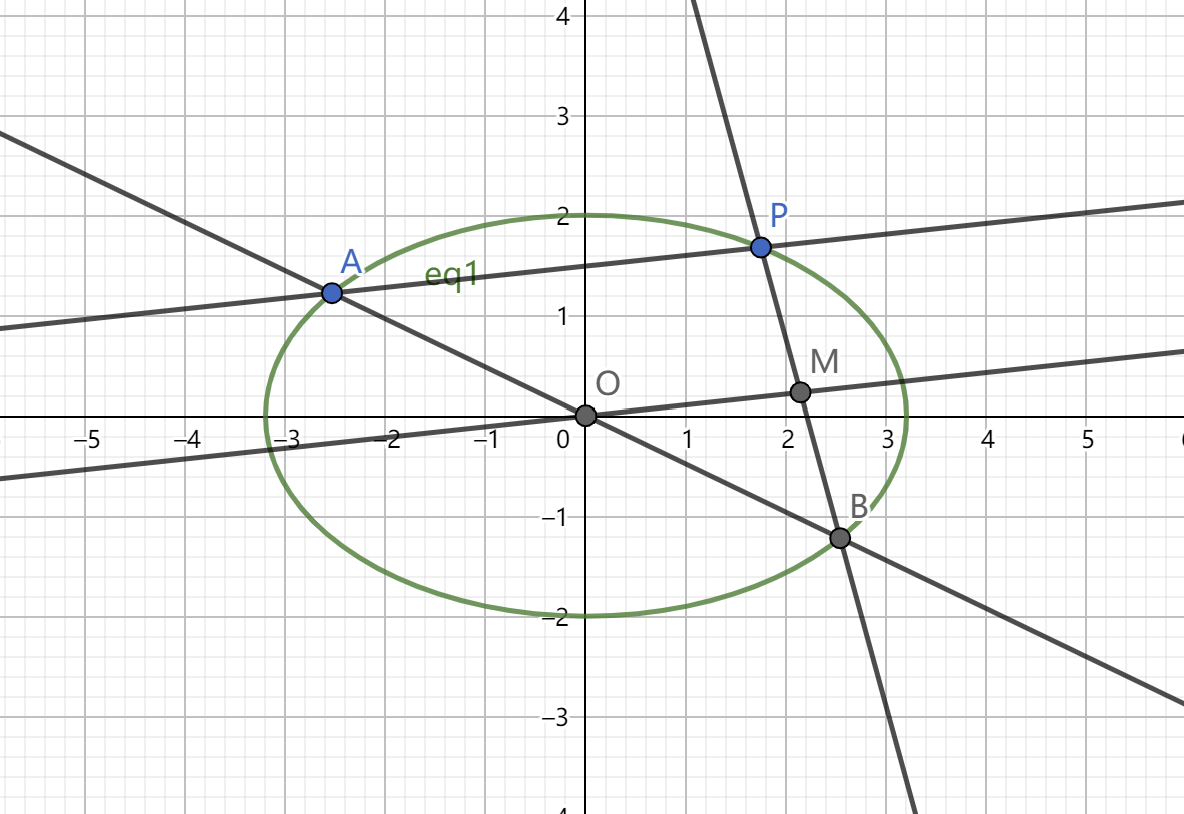

更一般地，以在 \(x\) 轴上的椭圆为例，对于任意一条过原点的直线与椭圆交于两点（此两点必关于原点对称）设为 \(A(x_0,y_0)\) ，\(B(-x_0,-y_0)\) 则对于椭圆上任意一点 \(P(m,n)\) ，都有 \(k_{PA}\times k_{PB}=k_{OM} \times k_{PB}=-\dfrac{b^2}{a^2}=e^2-1\) 成立。

证明如下：

​ \(\because\) \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)

​ \(\therefore\) \(b^2x^2+a^2y^2=a^2b^2\)

​ \(\therefore a^2y^2=a^2b^2-b^2x^2\)

​ \(\therefore n^2=b^2-\dfrac{b^2m^2}{a^2}\) \(\therefore y_0^2=b^2-\dfrac{b^2x_0^2}{a^2}\)

​ 表示 \(k_{PA} \times k_{PB}=\dfrac{(n-y_0)(n+y_0)}{(m-x_0)(m+x_0)}\) \(=\dfrac{n^2-{y_0}^2}{m^2-{x_0}^2}\) 将 \(n^2\) 与 \(y_0^2\) 代入即可得 \(k_{PA}\times k_{PB}=-\dfrac{b^2}{a^2}=e^2-1\)

​ 又\(\because\) \(O\) 为 \(AB\) 中点 ，\(M\) 为 \(PB\) 中点

​ $\therefore $ \(OM\) 为 $\triangle APB $ 的中位线

​ \(\therefore k_{PA}\times k_{PB}=k_{OM} \times k_{PB}=-\dfrac{b^2}{a^2}=e^2-1\)

2.双曲线：双曲线第三定义与椭圆同理，只不过注意斜率之积变为 \(\dfrac{b^2}{a^2}\) 。

3.从仿射变换的视角理解椭圆的第三定义（椭圆中的“垂径定理”），以焦点在 \(x\) 轴上为例。则椭圆相当于圆的横坐标不变，纵坐标变为原来的 \(\dfrac{b}{a}\) 也可得到 \(k_{PA}\times k_{PB}=-\dfrac{b^2}{a^2}=e^2-1\) 。同理，如果焦点在 \(y\) 轴上的椭圆，只需要保持纵坐标不变，横坐标变为原先的 \(\dfrac{b}{a}\) 。

1.圆的参数方程： \(\begin{cases}x=a+r\cos \theta\\y=b+r\sin\theta\end{cases}\)

2.椭圆的参数方程：有了仿射变换的思考，椭圆的参数方程可以说是呼之欲出。\(\begin{cases}x=a\cos\theta\\y=b\sin\theta\end{cases}\) 或 \(\begin{cases}x=b\cos\theta\\y=a\sin\theta\end{cases}\) 。需要注意的是此处的 \(\theta\) 角并不是椭圆上一点与原点连线的倾斜角，而是需要在仿射变换前找到对应的倾斜角。

3.双曲线的参数方程：应用不多，了解即可。\(\begin{cases}x=\dfrac{a}{\cos\theta}\\y=b\sin\theta\end{cases}\) ，其中 \(\theta\) 为参数。

4.抛物线的参数方程：以 \(y^2=2px\) 为例，则该抛物线的参数方程为 \(\begin{cases}x=2pt^2\\y=2pt\end{cases}\) ，其中 \(t\) 为参数，其意义为抛物线上除顶点外的任意一点到原点连线的斜率的倒数。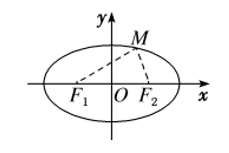

焦点三角形：以圆锥曲线的两焦点为底边，第三点为圆锥曲线上任意一点，图示 $\triangle MF_1F_2 $ 即为一个焦点三角形。

在椭圆中，对于焦点三角形，有\(C_{\triangle MF_1F_2}=2a+2c\) ，\(S_{\triangle MF_1F_2}=b^2\tan{ \dfrac{\theta}{2}}\) ，其中 \(\angle F_1MF_2=\theta\)

证明过程如下：

​ 不妨设 \(C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) ，\(|MF_1|=m\) ，\(|MF_2|=n\)

​ 由余弦定理可得，\(4c^2=4a^2-2mn(1+cos\theta)=(m+n)^2-2mn(1+cos\theta)\)

​ 即 \(4c^2=4a^2-2mn(1+cos\theta)\) 即 \(mn=\dfrac{2b^2}{1+cos\theta}\)

​ 根据正弦定理，\(S_{\triangle MF_1F_2}=\dfrac{1}{2} \cdot \dfrac{2b^2}{1+cos\theta} =b^2\tan{ \dfrac{\theta}{2}}\)

同理可得，在双曲线中，焦点三角形的面积 \(S_{\triangle MF_1F_2}=b^2\cot{ \dfrac{\theta}{2}}\) ，其中 \(\angle F_1MF_2=\theta\)

本内容下均以 \(C_1:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) 或者 \(C_2:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\) 为例

1.椭圆中： 共离心率的椭圆可以设为：\(C:\dfrac{x^2}{\lambda a^2}+\dfrac{y^2}{\lambda b^2}=1\)，\(\lambda>0\) 或者 \(C:\dfrac{y^2}{\lambda a^2}+\dfrac{x^2}{\lambda b^2}=1\)，\(\lambda > 0\)

​ 共焦点的椭圆可以设为 ：\(C:\dfrac{x^2}{a^2+\lambda}+\dfrac{y^2}{b^2+\lambda}=1\) ，其中 \(\lambda > -b^2\) 且 \(\lambda \ne 0\)

2.双曲线中： 共渐近线的双曲线可以设为：\(C:\dfrac{x^2}{\lambda a^2}-\dfrac{y^2}{\lambda b^2}=1\)，\(\lambda\ne 0\)

​ 共离心率的双曲线可以设为：\(C:\dfrac{x^2}{\lambda a^2} - \dfrac{y^2}{\lambda b^2}=1\)，\(\lambda>0\) 或者 \(C:\dfrac{x^2}{\lambda a^2} - \dfrac{y^2}{\lambda b^2}=1\)，\(\lambda < 0\)

​ 共焦点的双曲线可以设为 ：\(C:\dfrac{x^2}{a^2-\lambda}+\dfrac{y^2}{b^2+\lambda}=1\) ，其中 \(-b^2b>0)\) ，有 \(|EF_1|=ex_1+a\)， \(|EF_2|=a-ex_1\)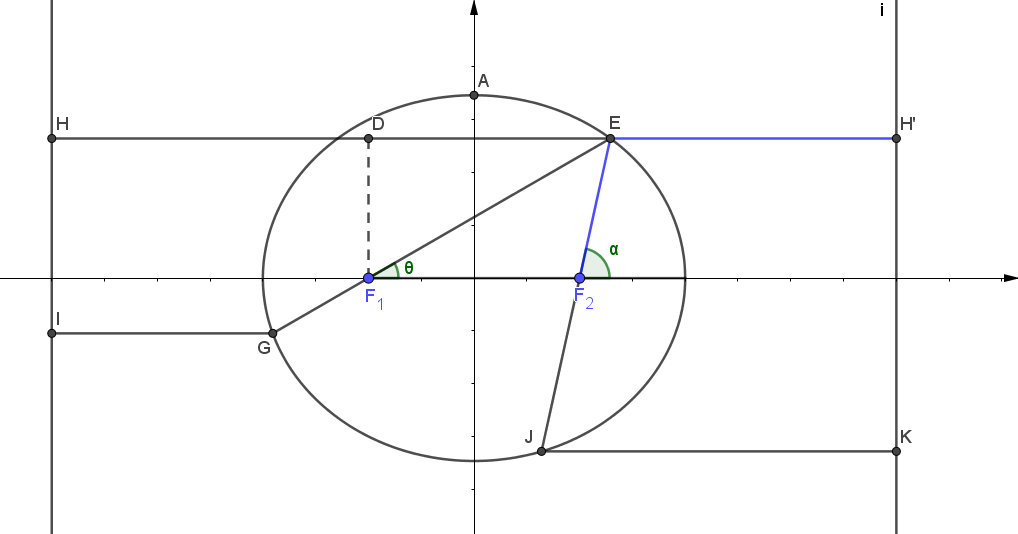

​ （1）坐标式：

​ 由椭圆的第二定义， \(\dfrac{|EF_1|}{|EH|}=e\)，\(\dfrac{|EF_2|}{|EH'|}=e\)

​ \(\therefore\) \(|EF_1|=\dfrac{c}{a}(x_1+\dfrac{a^2}{c})=ex_1+a\)，\(|EF_2|=\dfrac{c}{a}(\dfrac{a^2}{c}-x_1)=a-ex_1\)

​ \(\therefore |EG|=|EF_1|+|GF_1|\)

​ （2）角度式：求解角度式的时候注意从 \(F_1\) 向 \(DE\) 做垂可以更方便的利用 \(\theta\) 找关系

​ 由椭圆的第二定义， \(\dfrac{|EF_1|}{|EH|}=e\)，\(\dfrac{|EF_2|}{|EH'|}=e\)

​ \(\therefore |EF_1|=\dfrac{c}{a} \cdot (|EF_1 \cos \theta |-c+ \dfrac{a^2}{c} )=\dfrac{a^2}{b} + e|EF_1| \cos \theta\)

​ \(\therefore\) \(|EF_1|=\dfrac{\dfrac{b^2}{a}}{1-e\cos\theta}\) 同理可得， \(|GF_1|=\dfrac{\dfrac{b^2}{a}}{1+e\cos\theta}\)

​ \(\therefore\) \(|EG|=|EF_1|+|GF_1|=\dfrac{2\dfrac{b^2}{a}}{1-e\cos^2\theta}\)

2.双曲线：同理，只需注意准线的位置而导致的坐标表示时出现的变化。如图，设 \(M(x_1,y_1)\)，\(N(x_2,y_2)\)，双曲线 \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2}=1\) 计算过程此处不多赘述。计图中\(\angle MF_1F_2=\alpha\)，\(\angle H_2MF_2=\beta\)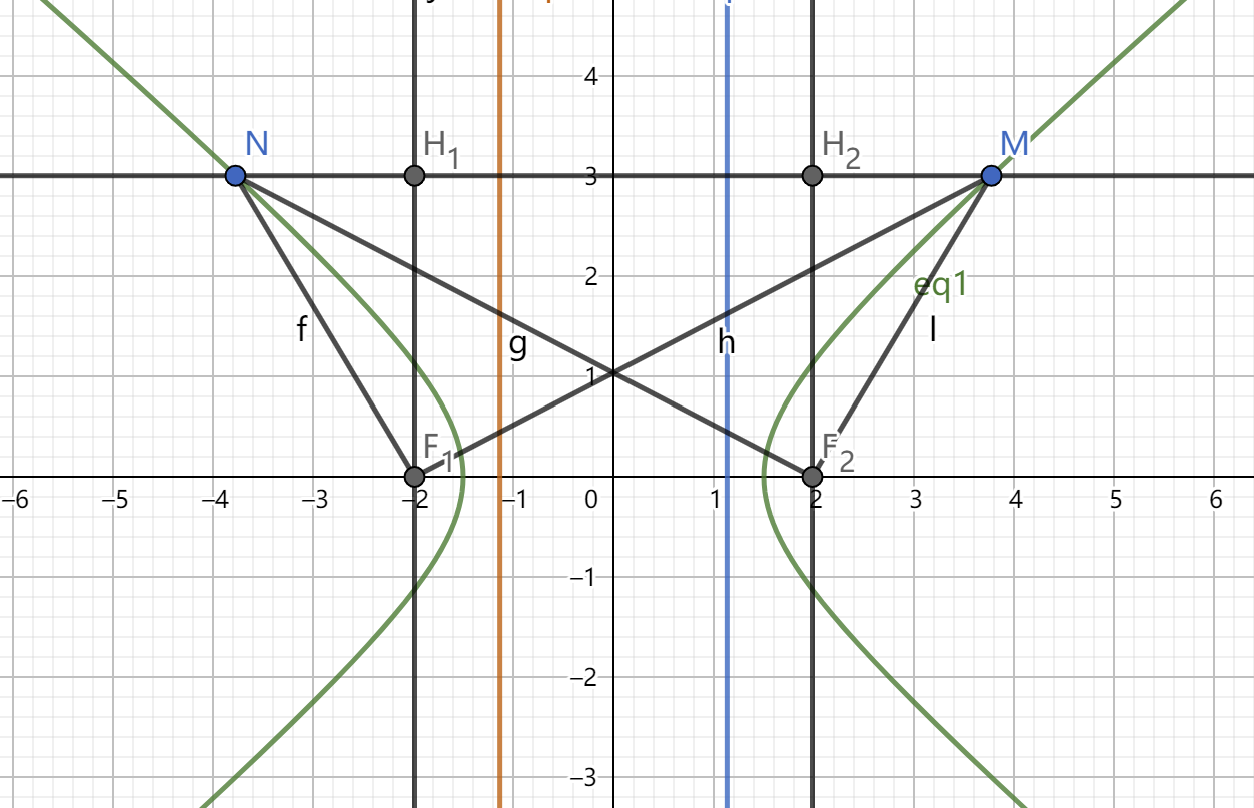

​ （1）坐标式：

​ \(|MF_1|=ex_1+a\)，\(|MF_2|=ex_1-a\)

​ \(|NF_1|=-ex_2-a\)，\(|NF_2|=-ex_2+a\)

​ （2）角度式：

​ \(|MF_1|=\dfrac{\dfrac{b^2}{a}}{e\cos\alpha-1}\)，\(|MF_2|=\dfrac{\dfrac{b^2}{a}}{1-e\cos\beta}\)

​ \(|NF_1|=\dfrac{\dfrac{b^2}{a}}{1-e\cos\beta}\) ， \(|NF_2|=\dfrac{\dfrac{b^2}{a}}{e\cos\alpha-1}\)

​ 同理，焦点弦长可以直接理解为两个焦半径之和。

3.抛物线：表示方法依然同理，只不过将 \(e\) 理解为 \(1\) 即可，但是抛物线有了更多引申的结论。不妨设抛物线 \(y^2=2px\) ，\(M(x_1,y_1)\)，\(N(x_2,y_2)\) 。抛物线中的焦点弦和焦半径更多用角度式来表示。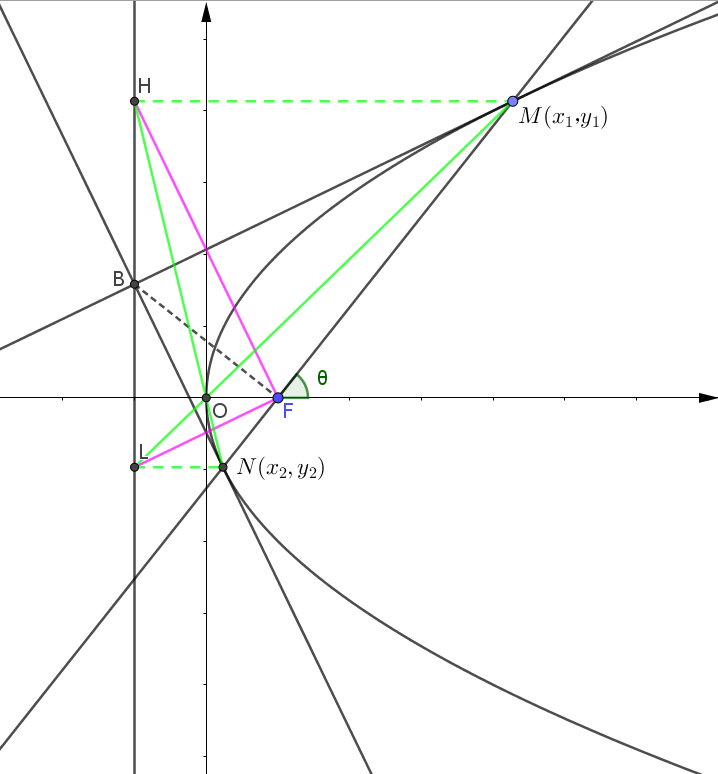

​ 根据抛物线的性质，\(|MF|=|MH|\)

​ \(\therefore\) \(|MF|\cos\theta+p=|MF|\)

​ \(\therefore\) \(|MF|=x_1+\dfrac{p}{2}=\dfrac{p}{1-\cos\theta}\)

​ 于是同理可得，\(|NF|=x_2+\dfrac{p}{2}=\dfrac{p}{1+\cos\theta}\) ，\(|MN|=x_1+x_2+p=\dfrac{2p}{sin^2\theta}\)

​ 不难看出以下几个结论：

​ ① \(\dfrac{1}{|MF|}+\dfrac{1}{|NF|}=\dfrac{2}{p}\) ，证明方法：直接利用上述结果计算。

​ ① \(x_1\cdot x_2=\dfrac{p^2}{4}\)，\(y_1\cdot y_2=-p^2\) 证明方法：可以设直线联立用韦达定理证明，不难算。

引申出的推论还有：

（1）以线段 \(MN\) 为直径的圆与抛物线的准线相切

（2）以焦半径为直径的圆与 \(y\) 轴相切

（3）以 \(HL\) 为直径的圆与焦点弦 \(MN\) 相切于焦点 \(F\)

（4）\(M,O,L\) 三点共线

（5）\(N,O,H\) 三点共线

1.抛物线的光学性质：从焦点射出的一条光线经抛物线反射后光线一定平行于 \(x\) 轴射出（针对于焦点在 \(x\) 轴正半轴的情况）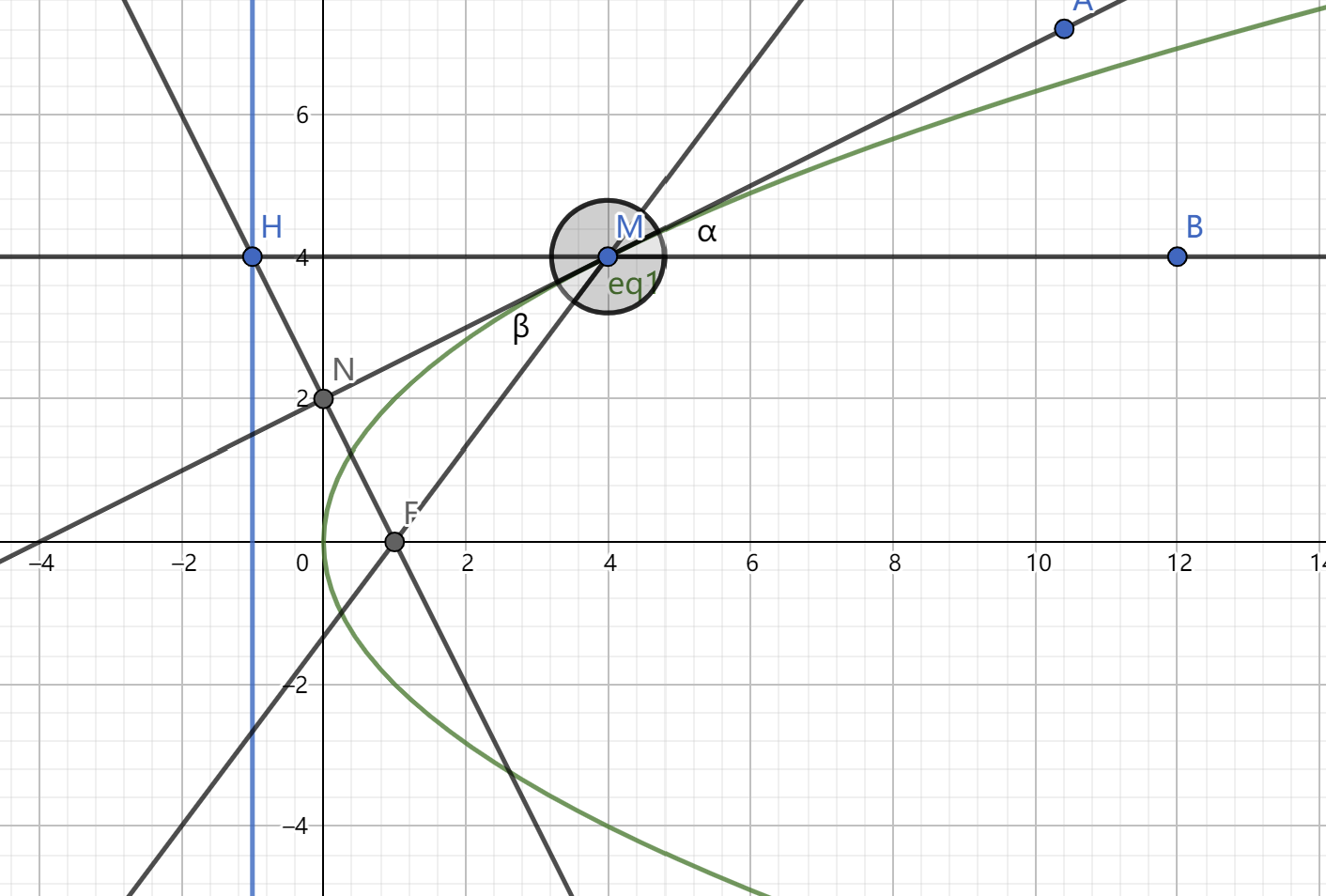

下面给出证明思路：

​ 为了证明上述结论，我们可以对光学性质进行变形，不妨变形为取抛物线上一点 \(M(x,y)\) 过点 \(M\) 做平行于 \(x\) 轴的一条直线交准线于点 \(H\) 连接 \(FH\) ，这样我们只需证明线段 \(HF\) 的中垂线（为证 \(\alpha\) 与 \(\beta\) 相等，所以需要将 \(\alpha\) 角对顶过去）与点 \(M\) 出的切线重合即可。

​ 所以我们利用 \(M\) 的坐标表示 \(H\) 的坐标，再利用点 \(H\) 与点 \(F\) 表示线段 \(HF\) 的中垂线，然后表示 \(M\) 点处的切线，可得两条线是重合的，于是我们证明了抛物线的光学性质。

2.椭圆的光学性质：从焦点射出的一条光线经椭圆反射一次后一定经过另一焦点。证明方法可以用角平分线定理优化计算。

3.双曲线的光学性质：从焦点射出的一条光线反射后光线的反向延长线经过另一焦点。暂无更好的证明方法，待补充。

谈到抛物线的光学性质就不得不提及双曲线中渐近线的各种性质。

1.渐近线常用性质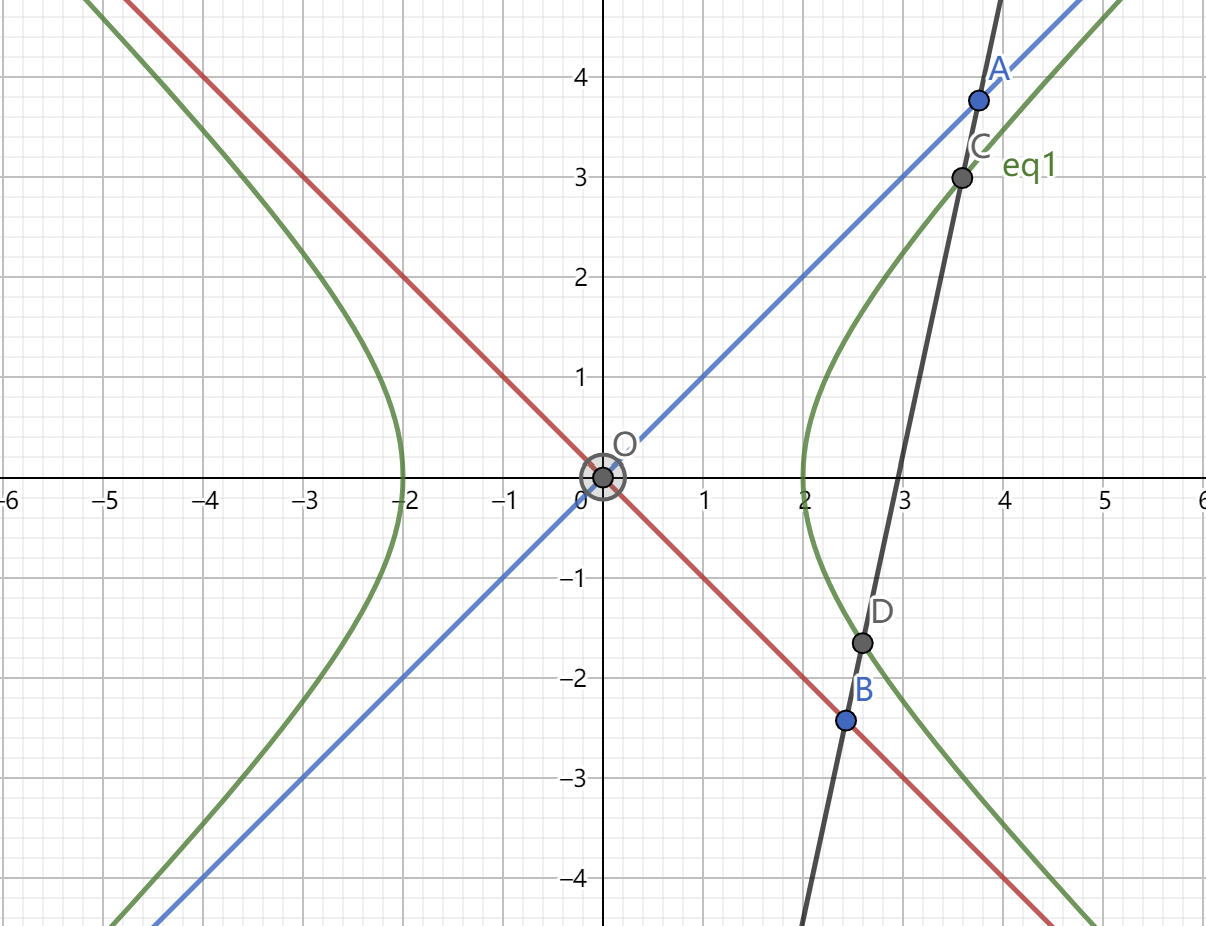

​ （1）\(AC=BD\) ,即线段 \(AB\) 的中点与线段 \(CD\) 的中点重合

​ （2）设线段 \(AB\) 的中点为 \(M\) 则 \(M\) 点也满足圆锥曲线中的垂径定理，即 \(k_{AB} \cdot k_{OM}=e^2-1\) 简要的证明思路就是找中心对称点，利用三角形中位线得到平行，进而得到此性质。

​ （3）设 \(\angle AOB=2\alpha\) ，\(A(x_1,y_1)\) ，\(B(x_2,y_2)\) ，则 \(S_{\triangle AOB}=|x_1x_2|\cdot \tan \alpha=|x_1x_2| \cdot \dfrac{b}{a}\)

​ 证明： \(OA=\dfrac{|x_1|}{\cos \alpha }\) ，\(OB=\dfrac{|x_2|}{\cos \alpha}\)

​ \(S_{\triangle AOB}=\dfrac{1}{2} \cdot OA\cdot OB\cdot \sin 2\alpha=\dfrac{|x_1||x_2| \cdot \sin 2\alpha}{2 \cos^2 \alpha }=\dfrac{|x_1||x_2| \cdot 2\sin \alpha \cos \alpha}{2 \cos^2 \alpha }=|x_1| \cdot |x_2| \cdot \tan \alpha\)

​ （4）设 \(\overrightarrow{AC}=\lambda \overrightarrow{CB}\) ，\(A(x_1,y_1)\) ，\(B(x_2,y_2)\) ，则有 \(x_1x_2=a^2 \cdot \dfrac{(1+\lambda)^2}{4\lambda}\) ，\(S_{\triangle AOB}=|x_1| \cdot |x_2| \cdot \tan \alpha=ab\cdot \dfrac{(1+\lambda)^2}{4\lambda}\)

​ 证明思路：利用定比坐标公式表示出 \(C\) 点坐标，表示 \(A,B\) 在渐近线上，同时表示 \(C\) 点在椭圆上，即可得到该性质。

​ （5）焦点到渐近线的距离为 \(b\) 。

​ （6）半径为 \(a\) 的焦点与渐近线交于 \(P(\dfrac{a^2}{c} , \dfrac{ab}{c} )\)

​ （6）半径为 \(c\) 的焦点与渐近线交于 \(P(a,b)\) 。

2.渐进三角形

​ （1） \(P\) 是线段 \(AB\) 的中点，即 \(|PA|=|PB|\)

​ （2） 渐进三角形的面积为定值 \(S_{\triangle AOB}=ab\)

​ 证明思路：利用1.（4）结论即可

3.双曲线上点关于渐近线的四边形面积定值问题

​ （1）构成平行四边形面积定值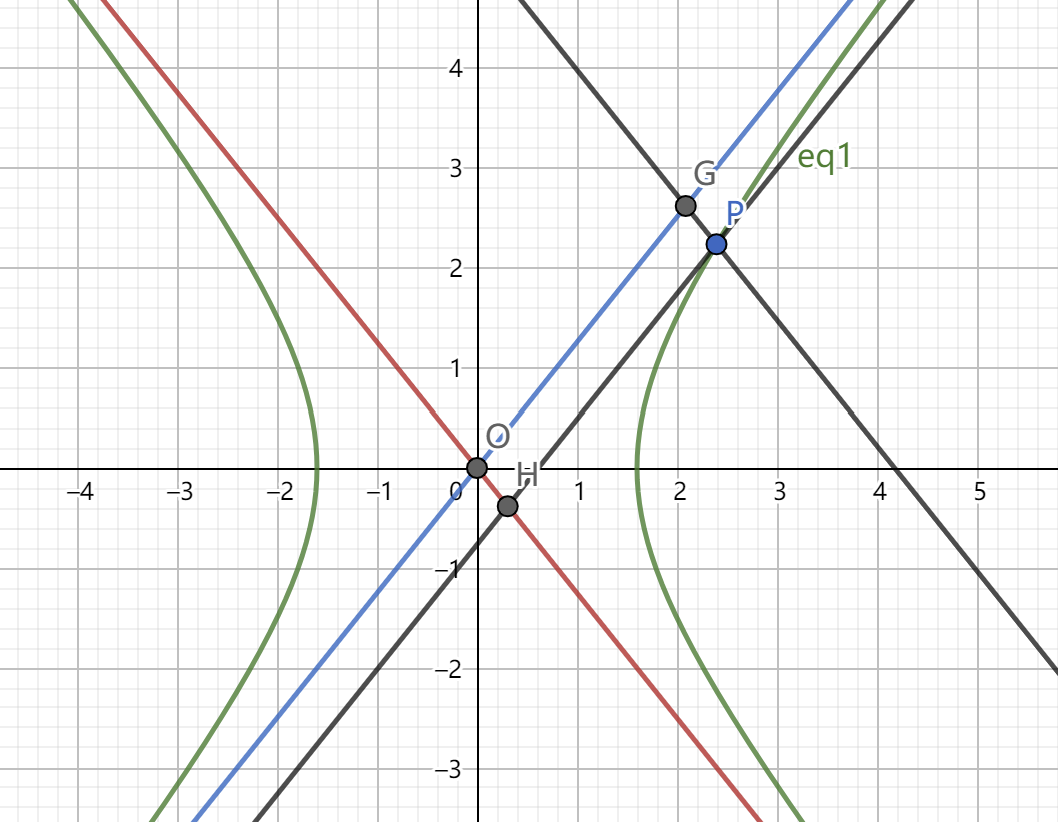

​ 如图有： \(x_Gx_H=\dfrac{a^2}{4}\)

​ 平行四边形 \(PGOH\) 的面积为定值 \(\dfrac{ab}{2}\)

​ （2）双曲线上的点到两渐近线距离之积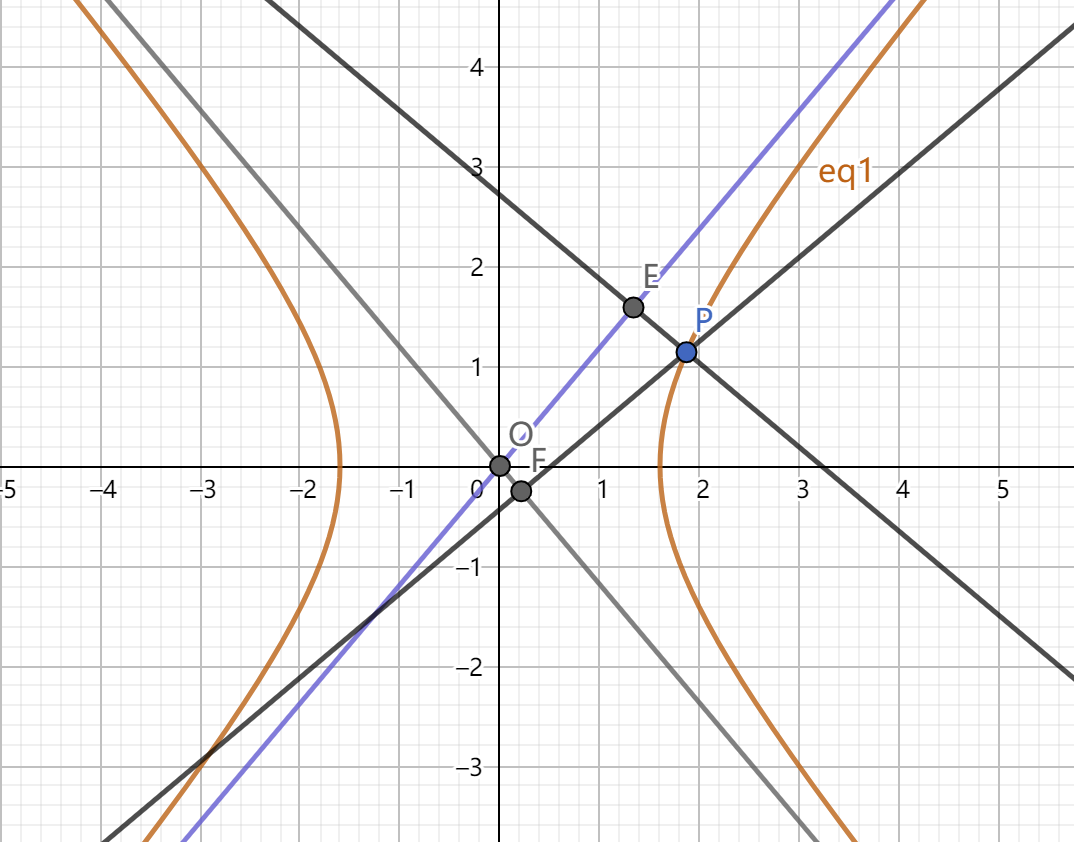

​ 则有 \(|PE|\cdot |PF|\) ，\(\overrightarrow{PE} \cdot \overrightarrow{PF}\) ，\(S_{\triangle PEF}\) 均为定值。

1.坐标系中的面积公式：

已知三角形三个点坐标，我们可以以任意一个顶点为原点，写出另外两个点的坐标，设为 \((x_1,y_1)\) 与 \((x_2,y_2)\) ，则此三角形的面积可以表示为 \(\dfrac{1}{2}|x_1y_2-x_2y_1|\)

2.截距坐标公式：

有了上面的三角形坐标公式我们就可以写出过两点 \(A,B\) 的直线与坐标轴的截距，与 \(x\) 轴的坐标公式为 \(\dfrac{x_1y_2-x_2y_1}{y_2-y_1}\) ，与 \(y\) 轴的坐标公式为 \(\dfrac{x_1y_2-x_2y_1}{x_1-x_2}\)

3.快速写过抛物线两点的直线方程：

设抛物线与直线交于 \(A(x_1,y_1),B(x_2,y_2)\) 两点，则直线 \(AB\) 的方程为 \(2px-(y_1+y_2)y+y_1y_2\) 。证明思路是 \(y_1,y_2\) 是方程 \(y^2-(y_1+y_2)y+y_1y_2\) 的两根，将 \(y^2\) 替换为 \(2px\) 即可。

4.四点共圆中的斜率之和为 \(0\) ：

若圆锥曲线上四点共圆，则这四个点构成的四边形对边对角线斜率之和均为 \(0\) 。证明思路：利用二次曲线系 $\lambda C_1+\mu C_2=C_3 $ ,然后因为这四个点共圆，所以令 \(x^2\) 项与 \(y^2\) 项的系数相等，并且令 \(xy\) 项系数为 \(0\) 即可。

5.焦点三角形的内切圆 ： 焦点三角形的内切圆的圆心在 \(x\) 轴上的投影恰好为双曲线的端点，证明联想切线长定理以及双曲线的定义。