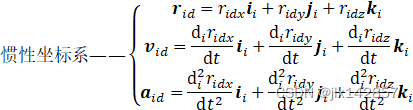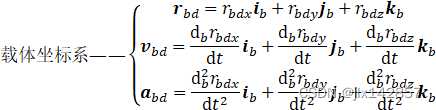平台式惯性导航系统简介（持续更新ing）

您所在的位置：网站首页 › 惯性导航系统组成有 › 平台式惯性导航系统简介（持续更新ing）

平台式惯性导航系统简介（持续更新ing）

2024-07-11 01:05| 来源: 网络整理| 查看: 265

惯性导航系统是利用惯性敏感器件，通过基准方向、初始位置等信息来确定运载体位置、姿态和速度的自主式航位推算系统。平台式惯性导航系统是与捷联式惯性导航系统相对应的一种导航方式。

前言

一、前备知识

1. 惯性导航常用坐标系

2.哥氏加速度

3. 坐标变换方法

（1）欧拉角法

（2）四元数法

4.加速度计与比力方程

5.误差对导航精度的影响

6.矢量叉乘的矩阵形式

二、指北方位惯导系统力学编排

1.平台指令角速度

2.速度方程

3.经纬度方程

4.高度通道

更新日志

前言

本文拟简要介绍平台式惯性导航系统（Platform Inertial Navigation System）。本文内容主要来源于作者本人的学习过程，参考书籍为秦永元编著的《惯性导航》(第三版)。本文将持续更新，逐步完善。

图1 参考书《惯性导航》

平台式惯性导航系统简称平台式惯导，根据百度百科，其为将惯性敏感器（陀螺仪Gyroscope以及加速度计Accelerometer）安装在一个稳定平台上，以平台坐标系为基准测量载体运动参数的惯导。平台式惯导系统中，采用机电控制的方法建立起相对稳定的物理实体平台，用于模拟载体所要求的导航坐标系。

图2 惯性导航平台装置

惯性导航平台视频（bilibili）

平台式惯导利用惯性平台隔离运载体的角运动，在导航坐标系旋转比较缓慢的情况下，导航计算机的解算负担较轻。在20世纪60-70年代，平台式惯导是在计算机技术没有充分发展的情况下的一种利用精密机械的导航替代方案，然而其缺点也十分明显，如结构复杂、体积大、重量重、可靠性差等。随着新一代的陀螺技术的日渐成熟，平台式惯导逐步被捷联式惯导所取代。然而，作为惯性导航领域里的经典工程实现，平台式惯导所渗透的思想可以说是永恒不灭的。

平台式惯性导航系统大致分为三种：1、指北方位惯导系统；2、自由方位惯导系统；3、游动方位惯导系统。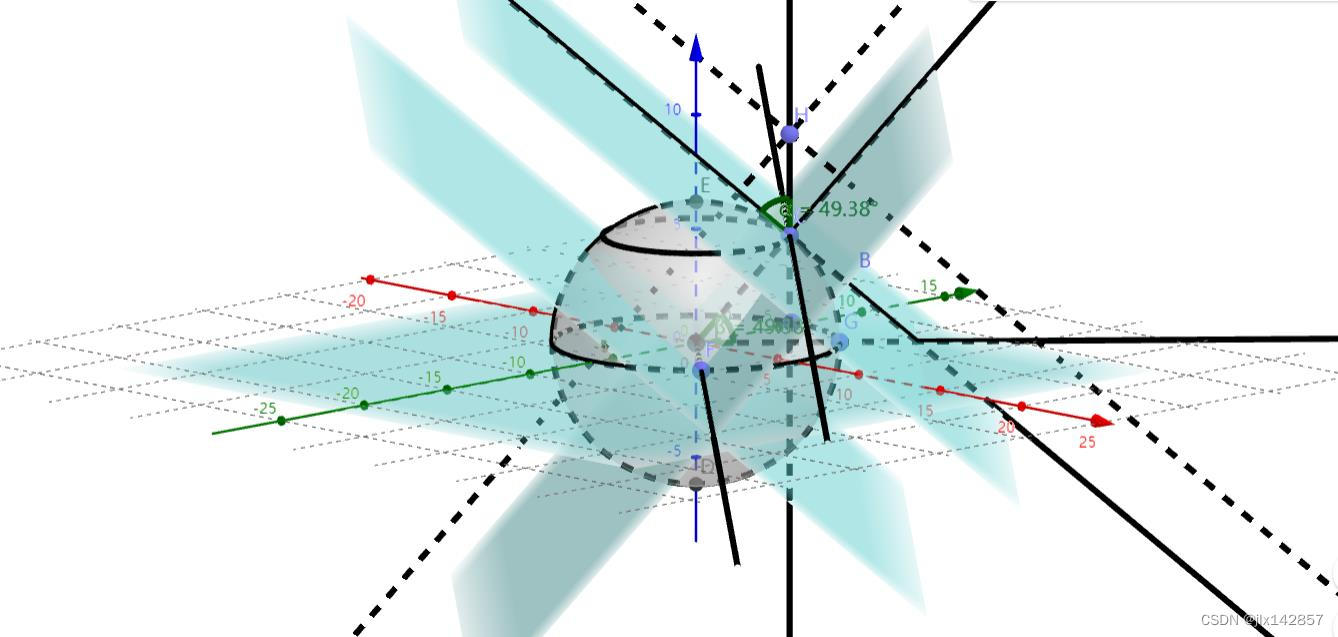

图3 惯性导航系统地球坐标系示意

一、前备知识 1. 惯性导航常用坐标系

首先，建立任何坐标系的前提是务必保证xyz三轴符合右手定则，即右手手掌心位于坐标系原点，四指伸向x轴正方向，随后握向y轴正方向，此时z轴正方向应与大拇指伸出的方向保持一致。

1、地心惯性坐标系 i：可用inertia(惯性)-i理解。

2、地球坐标系 e：原点位于地心，x轴穿越本初子午线与赤道的交点；z轴穿越地球北极点，y轴穿越东经90度子午线与赤道的交点。可用earth(地球)-e理解。

3、地理坐标系 g：原点位于运载体质心，xyz轴正方向分别指向运载体所处地理位置的东向、北向与天向（沿地球极轴向外）。可用geography(地理)-g理解。

4、导航坐标系 n：用于导航解算的参考坐标。

5、理想平台坐标系 T：导航坐标系理想化无误差的复现（跟踪）。或许可用平台简写PT的T理解（x）。

6、实际平台坐标系 P：由平台台体上的惯性仪器敏感轴确定，是导航坐标系理想化跟踪后的实际情况，相较于理想情况的T系存在平台失准角。或许可用平台简写PT的P理解（x）。

7、机体坐标系 b：原点位于飞机等运载体质心，xyz分别指向机体的右方、前方与上方。欧美和苏联在该系的使用上有所区别。可用body(载体)-b理解。

2.哥氏加速度

惯性导航中最重要的理论莫过于哥氏加速度（Coriolis Acceleration）理论。本节主要介绍描述物体牵连运动的哥氏加速度。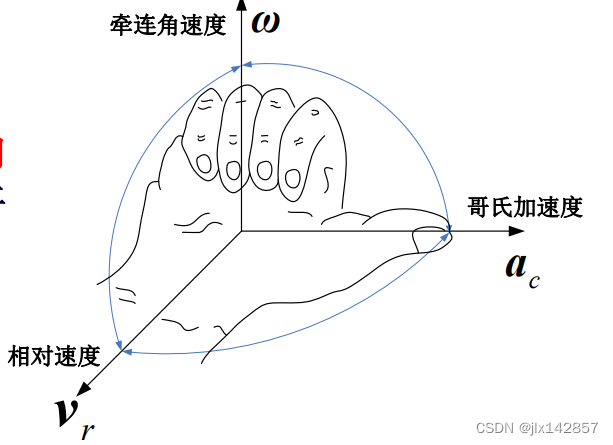

图4 牵连角速度示意图

哥氏加速度描述质点在运动坐标系中的相对运动与动坐标系之于惯性坐标系的牵连旋转运动两方面的相互影响。设惯性坐标系的位置固定，描述为 $\small I-x_i\ y_i\ z_i$ ；载体坐标系描述为 $\small B-x_b\ y_b\ z_b$ 。

当载体相对于惯性坐标系进行牵连旋转运动，该运动角速度设为 $\small \boldsymbol{\omega}_{ib}$ 。设质点 $\small \boldsymbol{d}$ 相对于惯性坐标系和载体坐标系的位置向量分别为 $\small \boldsymbol{r}_{id}$ , $\small \boldsymbol{r}_{bd}$ 。根据运动学公式，位置向量 $\small \boldsymbol{r}$ 对时间求一阶导和二阶导可以得到速度向量 $\small \boldsymbol{v}$ 及加速度向量 $\small \boldsymbol{a}$ ，故可建立 $\small \boldsymbol{d}$ 点在惯性坐标系和载体坐标系的运动学描述如下，其中 $\small \boldsymbol{i,j,k}$ 表示各坐标系 $\small \mathit{x,y,z}$ 方向的单位向量。

设惯性坐标系原点到载体坐标系原点的向量为 $\small \boldsymbol{r}_{ib}$ ，当牵连运动角速度 $\small \boldsymbol{\omega}_{ib}=0$ 时，两坐标系之间没有相对运动，质点 $\small \boldsymbol{d}$ 相对于两坐标系的运动向量表式是相同的。下面考虑存在牵连运动角速度 $\small \boldsymbol{\omega}_{ib}\neq 0$ 时质点的运动情况。对于 $\small \boldsymbol{r}_{ib}$ ，有 $\small \boldsymbol{r}_{id}=\boldsymbol{r}_{ib}+\boldsymbol{r}_{bd}$ 。等式两边在惯性坐标系中对时间求一阶导数，得到质点 $\small \boldsymbol{d}$ 在惯性坐标系的速度向量表式

$\small \frac{\mathrm{d_i\boldsymbol{r}_{id}} }{\mathrm{d} t}=\frac{\mathrm{d_i\boldsymbol{r}_{ib}} }{\mathrm{d} t}+\frac{\mathrm{d_i\boldsymbol{r}_{bd}} }{\mathrm{d} t}$

考察质点 $\small \boldsymbol{d}$ 在载体坐标系的位置向量对其在惯性坐标系下速度向量的影响，即式上式等号右端第二项，将其展开得

$\small \frac{\mathrm{d_i\textit{r}_{bd}} }{\mathrm{d} t}=\frac{\mathrm{d_i\textit{r}_{bdx}} }{\mathrm{d} t}\boldsymbol{i}_{b}+\frac{\mathrm{d_i\textit{r}_{bdy}} }{\mathrm{d} t}\boldsymbol{j}_{b}+\frac{\mathrm{d_i\textit{r}_{bdz}} }{\mathrm{d} t}\boldsymbol{k}_{b}+\textit{r}_{bdx}\frac{\mathrm{d_i\boldsymbol{i}_{b}} }{\mathrm{d} t}+\textit{r}_{bdy}\frac{\mathrm{d_i\boldsymbol{j}_{b}} }{\mathrm{d} t}+\textit{r}_{bdz}\frac{\mathrm{d_i\boldsymbol{k}_{b}} }{\mathrm{d} t}$

对于前三项而言，可以看做是无牵连运动的情况，即有

$\small \left (\frac{\mathrm{d_i\textit{r}_{bd}} }{\mathrm{d} t}\right )_{\boldsymbol{\omega}_{ib}=0}=\frac{\mathrm{d_i\textit{r}_{bdx}} }{\mathrm{d} t}\boldsymbol{i}_{b}+\frac{\mathrm{d_i\textit{r}_{bdy}} }{\mathrm{d} t}\boldsymbol{j}_{b}+\frac{\mathrm{d_i\textit{r}_{bdz}} }{\mathrm{d} t}\boldsymbol{k}_{b}=\frac{\mathrm{d_b\textit{r}_{bd}} }{\mathrm{d} t}$

而对于后三项，载体坐标系 $\small \mathit{x,y,z}$ 轴的单位向量在惯性坐标系下的导数受牵连角速度影响，有

$\small \frac{\mathrm{d_i\boldsymbol{i}_{b}} }{\mathrm{d} t}=\boldsymbol{\omega}_{ib}\times \boldsymbol{i}_{b}$

$\small \frac{\mathrm{d_i\boldsymbol{j}_{b}} }{\mathrm{d} t}=\boldsymbol{\omega}_{ib}\times \boldsymbol{j}_{b}$

$\small \frac{\mathrm{d_i\boldsymbol{k}_{b}} }{\mathrm{d} t}=\boldsymbol{\omega}_{ib}\times \boldsymbol{k}_{b}$

代入得

$\small \frac{d_ir_{bd}}{dt}=\frac{d_br_{bd}}{dt}+\mathbf{\omega}_{ib}\times\left(r_{bdx}\mathbf{i}_b+r_{bdy}\mathbf{j}_b+r_{bdz}\mathbf{k}_b\right)$

再由载体坐标系位置向量分解，代入得到位置向量的哥氏定理表达式

$\small \frac{d_ir_{bd}}{dt}=\frac{d_br_{bd}}{dt}+\mathbf{\boldsymbol{\omega}}_{ib}\times\boldsymbol{r}_{bd}$

进而得

$\small \frac{\mathrm{d_i\boldsymbol{r}_{id}} }{\mathrm{d} t}=\frac{\mathrm{d_i\boldsymbol{r}_{ib}} }{\mathrm{d} t}+\frac{\mathrm{d_b\boldsymbol{r}_{bd}} }{\mathrm{d} t}+\mathbf{\boldsymbol{\omega}}_{ib}\times\boldsymbol{r}_{bd}$

对式两端在惯性坐标系中对时间求导，得到质点 $\small \boldsymbol{d}$ 相对惯性坐标系的加速度向量表式

$\small \frac{d_i^2r_{id}}{dt^2}=\frac{d_i^2r_{ib}}{dt^2}+\frac{d_i}{dt}\left(\frac{d_br_{bd}}{dt}\right)+\frac{d_i}{dt}\left(\mathbf{\boldsymbol{\omega}}_{ib}\times\boldsymbol{r}_{bd}\right)$

对上式两段用哥氏定理，得

$\small \frac{d_i}{dt}\left(\frac{d_b\boldsymbol{r}_{bd}}{dt}\right)=\frac{d_b^2\boldsymbol{r}_{bd}}{dt^2}+\boldsymbol{\omega}_{ib}\times\frac{d_b\boldsymbol{r}_{bd}}{dt}$

$\small \frac{d_i}{dt}\left(\boldsymbol{\omega}_{ib}\times\boldsymbol{r}_{bd}\right)=\frac{d_b}{dt}\left(\boldsymbol{\omega}_{ib}\times\boldsymbol{r}_{bd}\right)+\boldsymbol{\omega}_{ib}\times\left(\boldsymbol{\omega}_{ib}\times\boldsymbol{r}_{bd}\right)$

对于牵连角速度 $\small \boldsymbol{\omega}_{ib}$ 而言，根据哥氏定理其关于时间的导数有

$\small \frac{d_b\boldsymbol{\omega}_{ib}}{dt}=\frac{d_i\boldsymbol{\omega}_{ib}}{dt}-\boldsymbol{\omega}_{ib}\times\boldsymbol{\omega}_{ib}=\frac{d_i\boldsymbol{\omega}_{ib}}{dt}=\frac{d\boldsymbol{\omega}_{ib}}{dt}$

可进一步得

$\small \frac{d_i}{dt}\left(\boldsymbol{\omega}_{ib}\times\boldsymbol{r}_{bd}\right)=\frac{d_b\boldsymbol{\omega}_{ib}}{dt}\times\boldsymbol{r}_{bd}+\boldsymbol{\omega}_{ib}\times\frac{d_b\boldsymbol{r}_{bd}}{dt}+\boldsymbol{\omega}_{ib}\times\left(\boldsymbol{\omega}_{ib}\times\boldsymbol{r}_{bd}\right)=\frac{d\boldsymbol{\omega}_{ib}}{dt}\times\boldsymbol{r}_{bd}+\boldsymbol{\omega}_{ib}\times\frac{d_b\boldsymbol{r}_{bd}}{dt}+\boldsymbol{\omega}_{ib}\times\left(\boldsymbol{\omega}_{ib}\times\boldsymbol{r}_{bd}\right)$

综合各式得载体的绝对加速度表式

$\small \frac{d_i^2r_{id}}{dt^2}=\frac{d_i^2r_{ib}}{dt^2}+\frac{d_b^2r_{bd}}{dt^2}+2\boldsymbol{\omega}_{ib}\times\frac{d_br_{bd}}{dt}+\frac{d\boldsymbol{\omega}_{ib}}{dt}\times\boldsymbol{r}_{bd}+\boldsymbol{\omega}_{ib}\times\left(\boldsymbol{\omega}_{ib}\times\boldsymbol{r}_{bd}\right)$

为了便于推导，令载体坐标系与惯性坐标系原点重合，并将牵连角速度 $\small \boldsymbol{\omega}_{ib}$ 写为Ω，则上式化为

$\small \boldsymbol{a}_{id}$ ——绝对加速度，表示质点 $\small \boldsymbol{d}$ 相对于惯性坐标系的加速度

$\small \boldsymbol{a}_{bd}$ ——相对加速度，表示质点 $\small \boldsymbol{d}$ 相对于载体坐标系的加速度

Ω ——载体坐标系相对于惯性坐标系的旋转角速度

$\small \boldsymbol{v}_{bd}$ ——表示质点 $\small \boldsymbol{d}$ 相对于载体坐标系的速度

2Ω $\small \times\boldsymbol{v}_{bd}$ ——哥氏加速度

r ——表示质点 $\small \boldsymbol{d}$ 相对于坐标系原点的位置向量

dΩ/dt×r ——表示质点 $\small \boldsymbol{d}$ 的牵连切向加速度

Ω×r ——表示质点 $\small \boldsymbol{d}$ 的牵连向心加速度

此即简化的加速度哥氏定理。

3. 坐标变换方法

尽管与高等代数、矩阵分析、现代控制理论等其他学科中的一些概念相类似，但在惯性导航理论中，坐标和坐标系的概念有必要着重重申。

所谓坐标，即是为确定空间中一点的位置，按规定方法选取的有次序的一组数据；而所谓坐标系，则是一个能够使得系统中的每一个点和一组n个标量构成一一对应关系的n维系统。

对于我们的任务——导航而言，其恰恰以精确地描述运载体的运动轨迹为目标，明确坐标和坐标系的意义之重大不言而喻。因此在惯性导航理论中，绪论后的第一个学习内容往往是坐标变换，即描述不同坐标系间转化的数学方法。关于坐标系之间的转化，一般有平动和转动两种情况。相信大家不难相信，平动的情况较为简单，仅仅只是把初始坐标系的原点搬移到新坐标系的原点处，空间中相同点的两坐标系中的坐标变化可以用向量的加法描述；而旋转的情况相比之下较为复杂。

对于坐标系的旋转变换，比较基础的方法是欧拉角法，稍进阶的方法是四元数法，如下。

（1）欧拉角法

请试想一个普通的空间坐标系 $\small O-X_1Y_1Z_1$ ，将 $\small X_1$ 和 $\small Y_1$ 两个轴按照我们最习惯的方式画在平铺的纸面上，此时 $\small Z_1$ 轴应当指向空中。现在俯瞰纸面，应是如下情景：

图5 初始坐标系O-X1Y1Z1

设想一空间矢量 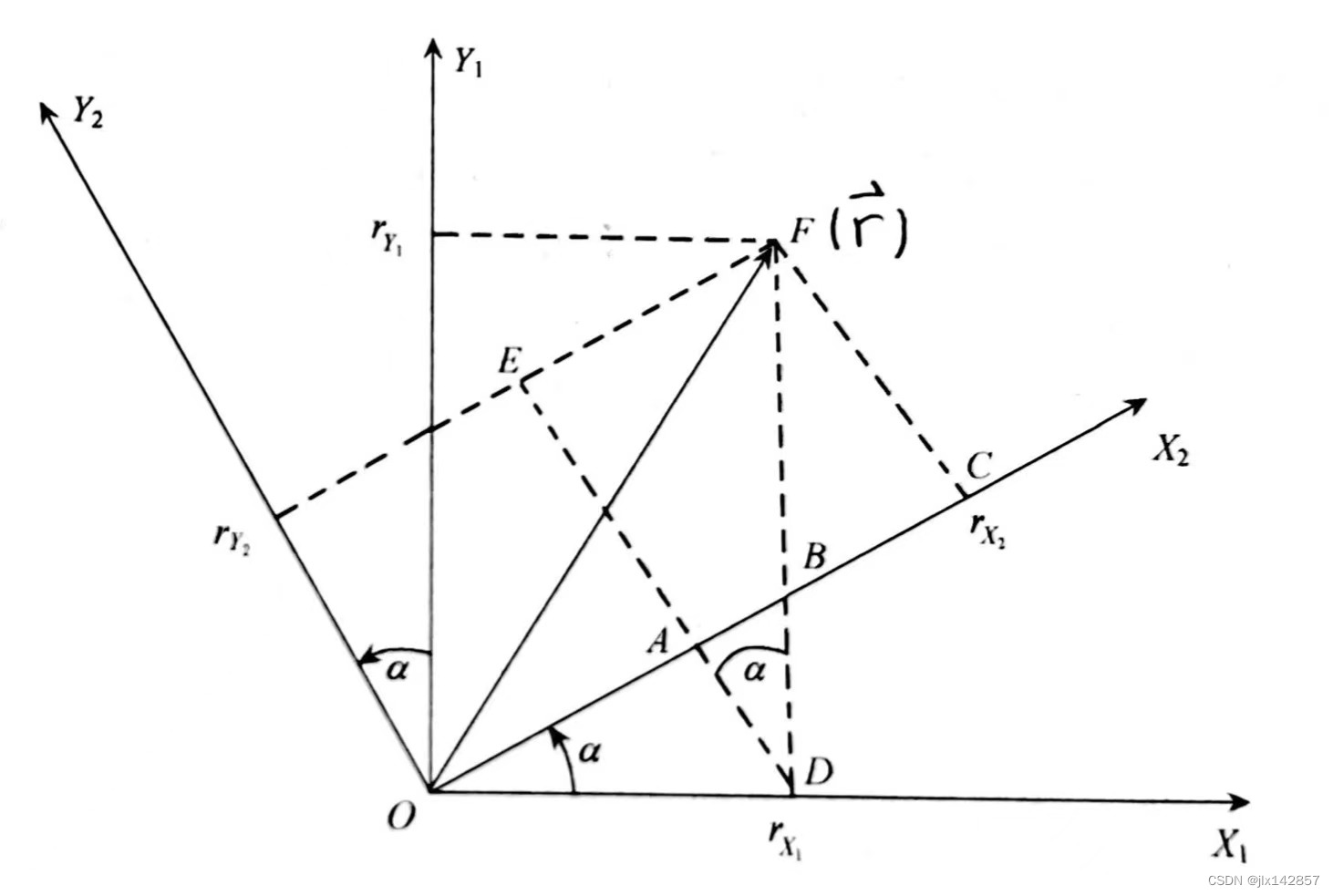$\small \boldsymbol{r}$ ，其在上述坐标系下的投影为 $\small \left ( r_{x1},r_{y1},r_{z1} \right )$ 。现将坐标系 $\small O-X_1Y_1Z_1$ 沿 $\small O-Z_1$ 旋转 $\small \alpha$ 角得到空间坐标系 $\small O-X_2Y_2Z_2$ ，空间矢量 $\small \boldsymbol{r}$ ，在新坐标系下的投影为 $\small \left ( r_{x2},r_{y2},r_{z2} \right )$ 。由于旋转轴为 $\small O-Z_1$ ，不难理解 $\small \boldsymbol{r}$ 的 $\small Z$ 分量不变，即有 $\small r_{z2}=r_{z1}$ 。此时情景如下：

图6 旋转后坐标系

考察坐标 $\small \left ( r_{x2},r_{y2},r_{z2} \right )$ 与 $\small \left ( r_{x1},r_{y1},r_{z1} \right )$ 之间的转换关系，根据几何知识，不难得出如下等式。

$\small r_{x2}=OA+AB+BC=OD\cos{\alpha}+FD\sin{\alpha}=r_{x1}\cos{\alpha}+r_{y1}\sin{\alpha}$

$\small r_{y2}=DE-AD=DF\cos{\alpha}-OD\sin{\alpha}=r_{y1}\cos{\alpha}-r_{x1}\sin{\alpha}$

再加上之前得到的 $\small r_{z2}=r_{z1}$ ，得到坐标变换的矩阵形式。

$\small \begin{bmatrix} r_{x2}\\ r_{y2}\\ r_{z2} \end{bmatrix}=\begin{bmatrix} \cos{\alpha} &\sin{\alpha} &0 \\ -\sin{\alpha} & \cos{\alpha} & 0\\ 0 &0 & 1 \end{bmatrix}\begin{bmatrix} r_{x1}\\ r_{y1}\\ r_{z1} \end{bmatrix}$

可将上式简化记为

$\small \boldsymbol{r}^2=\boldsymbol{C}_1^2\boldsymbol{r}^1$

其中 $\small \boldsymbol{C}_1^2$ 表示矢量在坐标系1经旋转至坐标系2的坐标变换，称为转换矩阵，运算方法为右乘原坐标系下坐标。特别地，上述 $\small \boldsymbol{C}_1^2$ 具体为沿 $\small Z$ 轴旋转的坐标转换矩阵。同理有 $X$ 轴和 $Y$ 轴的情况，请看下面更为复杂的例子。

在此之前，请让我们思考一个和欧拉角有关的结论：从一个坐标系到另一个坐标系的任何复杂的角位置变换过程都可以看做是三次欧拉角变换的复合。例如，运载体的空间姿态变化可以视作其机体坐标系（详见“惯性导航常用坐标系”一节）依次绕航向轴、俯仰轴、横滚轴做基本旋转后的复合结果。请看《惯性导航》一书中的下例：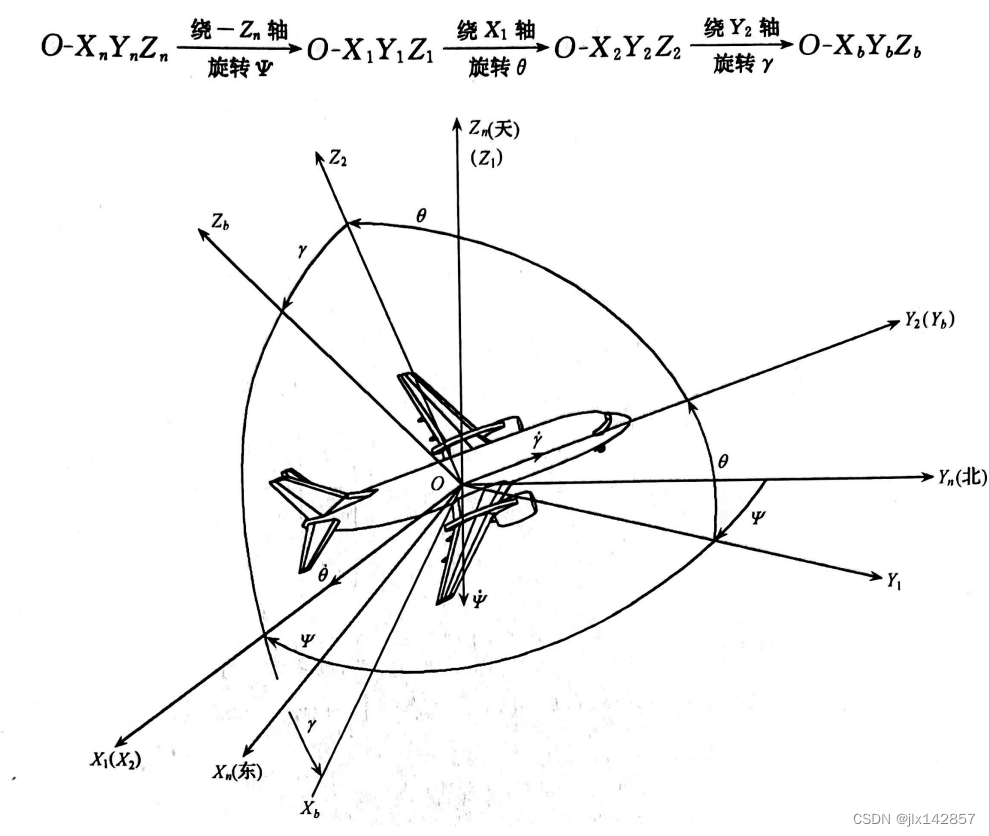

图7 地理-机体坐标系的三次欧拉角变换

图中，以 $\small n$ 为下标的坐标系为地理坐标系， $\small X_n$ 指向机体所在的地理方位东向、 $\small Y_n$ 指向地理方位北向、 $\small Z_n$ 沿地轴向外指向天向（三个方向简称“东北天”）；以 $\small b$ 为下标的坐标系为机体坐标系， $\small X_b$ 指向飞机“右”向、 $\small Y_b$ 指向“前”向、 $\small Z_b$ 指向“上”向。

按照图中所示的旋转次序，每次旋转对应一个变换矩阵 $\small C$ 阵；正如同我们先前分析的绕 $\small Z$ 轴旋转的例子一样，三次旋转的变换矩阵应与之类似，如下。

$\small \boldsymbol{C}_n^1=\begin{bmatrix} \cos{\mathit{\Psi}} &-\sin{\mathit{\Psi}} &0 \\ \sin{\mathit{\Psi}} & \cos{\mathit{\Psi}} & 0\\ 0 &0 & 1 \end{bmatrix}$

$\small \boldsymbol{C}_1^2=\begin{bmatrix} 1&0 &0 \\ 0 & \cos{\mathit{\theta}} & \sin{\mathit{\theta}}\\ 0 &-\sin{\mathit{\theta}} & \cos{\mathit{\theta}} \end{bmatrix}$

$\small \boldsymbol{C}_2^b=\begin{bmatrix} \cos{\mathit{\gamma}}&0 &-\sin{\mathit{\gamma}} \\ 0 & 1 & 0\\ \sin{\mathit{\gamma}} & 0&\cos{\mathit{\gamma}} \end{bmatrix}$

需要注意的是，矩阵中正弦函数形式的元素，正负号应当与旋转角的方向相联系，不能一概而论；但是可以发现的规律是，欧拉角绕哪个轴旋转，其变换矩阵中该轴对应的行(列)种元素为0或1，而剩余的四个位置元素，左上和右下是余弦项，左下和右上是正弦向，符号由旋转角的旋转方向与三角函数诱导公式决定。显然，变换矩阵形式上均为反对称矩阵。

关于变换矩阵，必须提及其最重要的性质，即任何一个变换矩阵均为正交矩阵。现以上述绕 $\small Z$ 轴旋转的 $\small \mathit{\Psi}$ 阵为例（其他类似），考察该性质。

$\small (\boldsymbol{C}_n^1)^T=\begin{bmatrix} \cos{\mathit{\Psi}} &\sin{\mathit{\Psi}} &0 \\ -\sin{\mathit{\Psi}} & \cos{\mathit{\Psi}} & 0\\ 0 &0 & 1 \end{bmatrix}$

$\small \boldsymbol{C}_n^1(\boldsymbol{C}_n^1)^T=\begin{bmatrix} \cos{\mathit{\Psi}} &-\sin{\mathit{\Psi}} &0 \\ \sin{\mathit{\Psi}} & \cos{\mathit{\Psi}} & 0\\ 0 &0 & 1 \end{bmatrix}\begin{bmatrix} \cos{\mathit{\Psi}} &\sin{\mathit{\Psi}} &0 \\ -\sin{\mathit{\Psi}} & \cos{\mathit{\Psi}} & 0\\ 0 &0 & 1 \end{bmatrix}=\begin{bmatrix} 1 & 0 &0 \\ 0 &1 &0 \\ 0 & 0 & 1 \end{bmatrix}=\boldsymbol{E}$

故有下式成立

$\small (\boldsymbol{C}_n^1)^{-1}=(\boldsymbol{C}_n^1)^T$

即变换矩阵为正交矩阵，其两两正交的行(列)向量也足以佐证这一点。

相较于旋转过程，我们可能更关注坐标系旋转的始末状态。下面考虑由地理坐标系经过三次旋转后得到机体坐标系的综变换矩阵，也被称为姿态矩阵，用 $\small \boldsymbol{C}_n^b$ 表示。

$\small \boldsymbol{C}_n^b=\boldsymbol{C}_2^b\boldsymbol{C}_1^2\boldsymbol{C}_n^1=\begin{bmatrix} \cos{\mathit{\gamma}}&0 &-\sin{\mathit{\gamma}} \\ 0 & 1 & 0\\ \sin{\mathit{\gamma}} & 0&\cos{\mathit{\gamma}} \end{bmatrix}\begin{bmatrix} 1&0 &0 \\ 0 & \cos{\mathit{\theta}} & \sin{\mathit{\theta}}\\ 0 &-\sin{\mathit{\theta}} & \cos{\mathit{\theta}} \end{bmatrix}\begin{bmatrix} \cos{\mathit{\Psi}} &-\sin{\mathit{\Psi}} &0 \\ \sin{\mathit{\Psi}} & \cos{\mathit{\Psi}} & 0\\ 0 &0 & 1 \end{bmatrix}$

在对上式进行进一步处理之前，我们需要明确一件事：由于矩阵乘法运算有“左乘”和“右乘”之分，三次坐标变换对应的变换矩阵也不可随意相乘；具体原则为，将“先变换”的置右，“后变换”的置左（如上式，先进行 $\small Z$ 轴变换，故 $\small \mathit{\Psi}$ 阵在矩阵连乘的最右侧，其他阵按序左乘），按序依次相乘，方可得到正确的姿态矩阵。

合并上式计算结果，得

$\small \boldsymbol{C}_n^b=\begin{bmatrix} \cos\gamma\cos\mathit{\Psi}+\sin\gamma\sin{\mathit{\Psi}}\sin{\theta} &-\cos\gamma\sin\mathit{\Psi}+\sin\gamma\cos{\mathit{\Psi}}\sin{\theta} &-\sin\gamma\cos\theta \\ \sin\mathit{\Psi}\cos\theta &\cos\mathit{\Psi} \cos\theta &\sin\theta \\ \sin\gamma\cos\mathit{\Psi}-\cos\gamma\sin{\mathit{\Psi}}\sin{\theta} & -\sin\gamma\sin\mathit{\Psi}-\cos\gamma\cos{\mathit{\Psi}}\sin{\theta} & \cos\gamma\cos\theta \end{bmatrix}$

当三轴旋转角 $\small \mathit{\Psi},\theta,\gamma$ 不都为小角时，不同的旋转次序会使得旋转结果产生差异，而当三者都为小角时，忽略小角间的高阶小量(即cos近似为1，单个sin近似为小角(采用弧度制)，多个sin连乘近似为0)，得到如下结果

$\small \boldsymbol{C}_n^b=\begin{bmatrix} 1 & -\mathit{\Psi} & -\gamma \\ \mathit{\Psi} &1 & \theta\\ \gamma&-\theta & 1 \end{bmatrix}$

此时，旋转后坐标系的角位置与旋转次序无关。

综上可得坐标系旋转的一般关系，设坐标系 $\small P$ 偏离坐标系 $\small T$ 的偏离角 $\small \phi_x,\phi_y,\phi_z$ 均为小角，则有

$\small \boldsymbol{C}_T^P=\begin{bmatrix} 1 & \phi_z& -\phi_y \\ -\phi_z &1 & \phi_x\\ \phi_y&-\phi_x & 1 \end{bmatrix}$

（2）四元数法

待填充

4.加速度计与比力方程

众所周知，实现惯性导航必备的元器件是一系列被称作惯性器件的敏感元件，主要是陀螺仪和加速度计。其中陀螺仪主要负责测量载体角速度，而加速度计则另有分工。

对于加速度计的职能，我们可以顾名思义，但是别太彻底。加速度计，简称“加计”，其输出与载体运动加速度成一定关系的信号，其输出信号的单位与性质与“加速度”相一致，但实际是输出一个名为“比力”的物理量而非载体的运动加速度。而比力，则表征载体相对惯性空间的绝对加速度和引力加速度之差。

设加速度计质量块质量为 $\small m$ ，位置矢量 $\small \boldsymbol{R}$ ，其受地球引力 $\small m\boldsymbol{G}$ ，受其他外力 $\small \boldsymbol{F}$ ，其中 $\small \boldsymbol{G}$ 表示引力加速度。由牛顿第二定律，有

$\small \boldsymbol{F}+m\boldsymbol{G}=m\frac{\textup{d}_i^2\boldsymbol{R}}{\textup{d}t^2}$

需要提示的是，微分运算符 $\small \textup{d}$ 的下标 $\small i$ 表示在惯性系下的微分；将等式两端除以质量 $\small m$ ，得到

$\small \boldsymbol{f}=\frac{\textup{d}_i^2\boldsymbol{R}}{\textup{d}t^2}-\boldsymbol{G}$

其中

$\small \boldsymbol{f}=\frac{\boldsymbol{F}}{m}$

此即比力，表征单位质量上作用的非引力外力，或载体相对惯性空间的绝对加速度和引力加速度之差。

若将矢量相对惯性坐标系 $\small i$ 求其对时间的变化率为绝对变化率，矢量在地球坐标系 $\small e$ 的投影对时间的变化率称为相对变化率，则根据哥氏定理，有

$\small \frac{\textup{d}_i\boldsymbol{R}}{\textup{d}t}=\frac{\textup{d}_e\boldsymbol{R}}{\textup{d}t}+\boldsymbol{\omega}_{ie}\times\boldsymbol{R}$

式中 $\small \boldsymbol{\omega}_{ie}$ 表示地球坐标系相对与惯性坐标系的转动角速度；式中 $\small \frac{\textup{d}_e\boldsymbol{R}}{\textup{d}t}$ 是在地球上观察到的位置矢量的变化率，即载体相对地球的运动速度，简称为地速，记为 $\small \boldsymbol{V}_{eT}$ ，进而将上式改写如下：

$\small \frac{\textup{d}_i\boldsymbol{R}}{\textup{d}t}=\boldsymbol{V}_{eT}+\boldsymbol{\omega}_{ie}\times\boldsymbol{R}$

再次对上式在惯性坐标系下两边取微分，以求得绝对变化率，得

$\small \frac{\textup{d}_i^2\boldsymbol{R}}{\textup{d}t^2}=\frac{\textup{d}_i\boldsymbol{V}_{eT}}{\textup{d}t}+\frac{\textup{d}_i}{\textup{d}t}\left (\boldsymbol{\omega}_{ie}\times\boldsymbol{R} \right )=\frac{\textup{d}_i\boldsymbol{V}_{eT}}{\textup{d}t}+\frac{\textup{d}_i\boldsymbol{\omega}_{ie}}{\textup{d}t}\times\boldsymbol{R}+\boldsymbol{\omega}_{ie}\times\frac{\textup{d}_i\boldsymbol{R}}{\textup{d}t}$

由于 $\small \boldsymbol{\omega}_{ie}$ 表示的地球转速近似恒定，故其对时间的微分为0，消去得

$\small \frac{\textup{d}_i^2\boldsymbol{R}}{\textup{d}t^2}=\frac{\textup{d}_i\boldsymbol{V}_{eT}}{\textup{d}t}+\boldsymbol{\omega}_{ie}\times\frac{\textup{d}_i\boldsymbol{R}}{\textup{d}t}$

取平台坐标系 $\small T$ 为动坐标系，对等式右端第一项使用哥氏定理，即

$\small \frac{\textup{d}_i\boldsymbol{V}_{eT}}{\textup{d}t}=\frac{\textup{d}_T\boldsymbol{V}_{eT}}{\textup{d}t}+\boldsymbol{\omega}_{iT}\times\boldsymbol{V}_{eT}$

根据矢量关系，有 $\small \boldsymbol{\omega}_{iT}=\boldsymbol{\omega}_{ie}+\boldsymbol{\omega}_{eT}$ ；综合各式，可得

$\small \frac{\textup{d}_i^2\boldsymbol{R}}{\textup{d}t^2}=\frac{\textup{d}_T\boldsymbol{V}_{eT}}{\textup{d}t}+\left ( 2\boldsymbol{\omega}_{ie}+\boldsymbol{\omega}_{eT} \right )\times\boldsymbol{V}_{eT}+\boldsymbol{\omega}_{ie}\times\left (\boldsymbol{\omega}_{ie}\times\boldsymbol{R} \right )$

再由

$\small \frac{\textup{d}_i^2\boldsymbol{R}}{\textup{d}t^2}=\boldsymbol{G}+\boldsymbol{f}$

得到

$\small \frac{\textup{d}_T\boldsymbol{V}_{eT}}{\textup{d}t}=\boldsymbol{f}+\boldsymbol{G}-\left ( 2\boldsymbol{\omega}_{ie}+\boldsymbol{\omega}_{eT} \right )\times\boldsymbol{V}_{eT}-\boldsymbol{\omega}_{ie}\times\left (\boldsymbol{\omega}_{ie}\times\boldsymbol{R} \right )$

事实上，式中的 $\small \boldsymbol{G}-\boldsymbol{\omega}_{ie}\times\left (\boldsymbol{\omega}_{ie}\times\boldsymbol{R} \right )$ 其实是我们熟悉的重力加速度，常用 $\small \boldsymbol{g}$ 表示，下面证明这一关系。请看《惯性导航》中的下图：

图8 地球旋转引起的向心加速度

根据矢量叉乘运算的右手定则及表达式，可得

$\small \left | \boldsymbol{\omega}_{ie}\times\boldsymbol{R} \right |=\omega_{ie}R\sin\left ( 90^{\circ}-L \right )=\omega_{ie}R\cos L$

$\small \left | \boldsymbol{\omega}_{ie}\times\left (\boldsymbol{\omega}_{ie}\times\boldsymbol{R} \right ) \right |=\omega_{ie}\cdot \omega_{ie}R\cos L\cdot \sin 90^{\circ}=\omega_{ie}^2R\cos L$

注意到矢量 $\small \boldsymbol{\omega}_{ie}\times\left (\boldsymbol{\omega}_{ie}\times\boldsymbol{R} \right)$ 的方向为载体在其所在地球纬度圈指向地球旋转轴，即向心加速度，记为 $\small \boldsymbol{a}_c$ 。

此时，请看《惯性导航》中的下图，回顾初中学习万有引力定律和地球重力加速度的场景。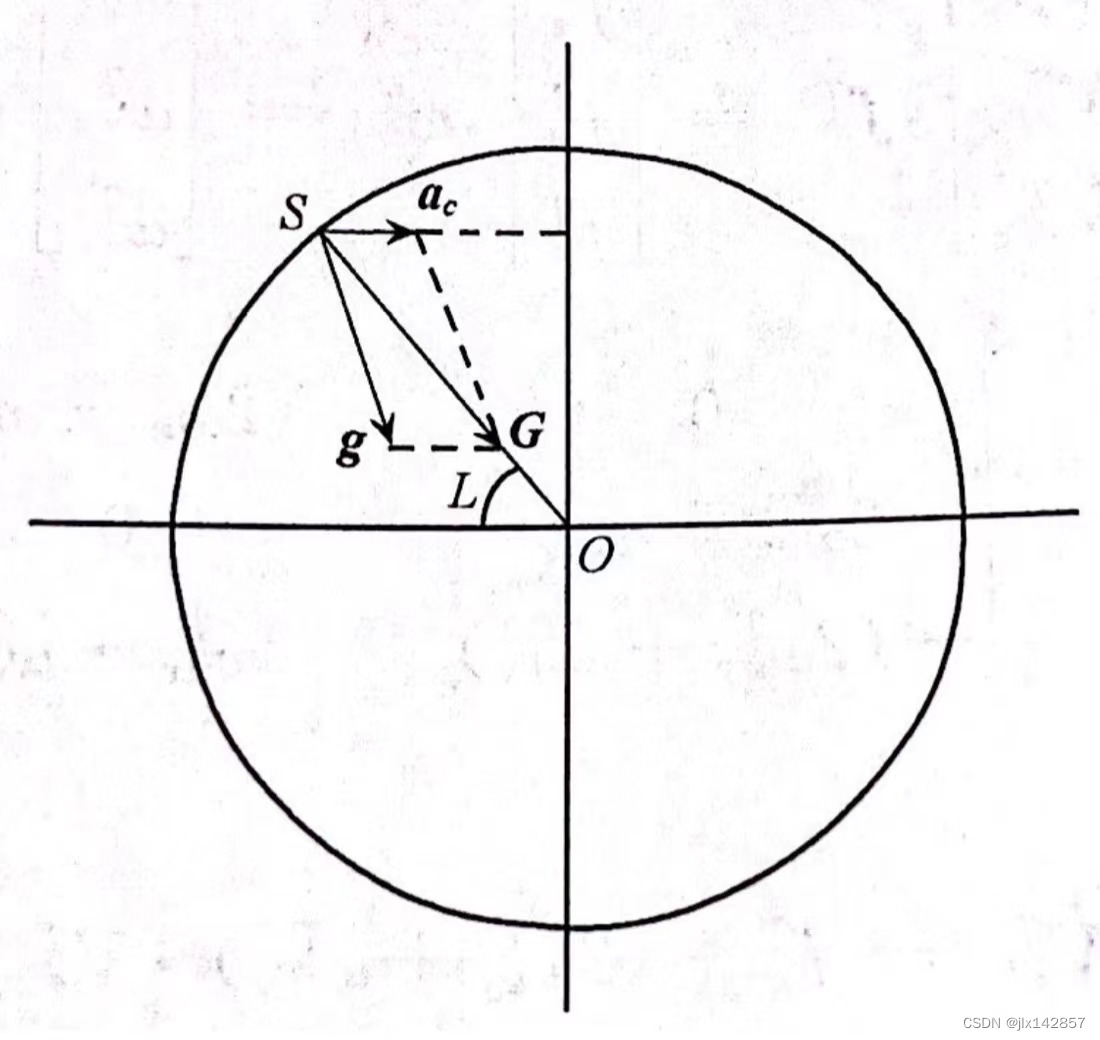

图9 引力加速度的两个分量

不再赘述，显然有

$\small \boldsymbol{g}=\boldsymbol{G}-\boldsymbol{a}_c=\boldsymbol{G}-\boldsymbol{\omega}_{ie}\times\left( \boldsymbol{\omega}_{ie}\times\boldsymbol{R} \right)$

综合各式，得到

$\small \boldsymbol{f}=\frac{\textup{d}_T\boldsymbol{V}_{eT}}{\textup{d}t}-\boldsymbol{g}+\left ( 2\boldsymbol{\omega}_{ie}+\boldsymbol{\omega}_{eT} \right )\times\boldsymbol{V}_{eT}$

此即惯性导航系统的基本方程——比力方程。

需要说明的是，比力方程左端的 $\small \boldsymbol{f}$ 是加速度计的测量值。在惯性器件原理和惯性导航系统课上，授课教授常问的问题是：加速度计的初始测量值中究竟包含着哪些加速度？

在回答这个问题之前，我们首先需要回答的是：我们使用加速度计的初心是什么？显然是获得载体的运动速度，而由于多数时候我们人在地球上，所以我们期望获得载体相对地球的运动速度，即地速。而根据比力方程，其中 $\small \frac{\textup{d}_T\boldsymbol{V}_{eT}}{\textup{d}t}$ 一项对时间积分即可得地速 $\small \boldsymbol{V}_{eT}$ ；审视比力方程右端的其他项，实际上均是我们不需要的，称为“有害加速度”。

有害加速度有三，其一，为哥氏加速度 $\small 2\boldsymbol{\omega}_{ie}\times\boldsymbol{V}_{eT}$ ，由载体相对于地球的运动和地球旋转的牵连运动引起；其二，为对地向心加速度 $\small \boldsymbol{\omega}_{eT}\times\boldsymbol{V}_{eT}$ ，使得载体保持在地球表面的圆周运动；其三，为当地重力加速度 $\small \boldsymbol{g}$ 。1个“需求”加3个“有害”，即回答了加速度计测量值的背后内涵。

5.误差对导航精度的影响

惯性导航系统的结构安装与惯性器件本身的加工不可避免的存在误差，下面对惯性器件本身的误差对系统导航精度的影响进行感性认识。

首先介绍结论，惯性导航系统的结构安装与惯性器件本身的加工所引起的误差将随时间累积，且陀螺仪的误差影响比加速度计大。

对于加速度计和陀螺仪而言，前者输出载体比力，后者输出载体运动角速度，二者均需要在一定时间内两次积分以得到载体的位置信息。积分运算是引起误差累积的罪魁祸首。

关于二者对惯性导航精度的影响孰轻孰重，请看下述分析。现设加速度计常值零偏为 $\small \delta$ ，陀螺仪常值漂移 $\small \varepsilon$ ，则根据运动学基本公式，可得下表

加速度计陀螺仪加速度计常值零偏 $\small \delta$ 陀螺仪常值漂移 $\small \varepsilon$ ————角度误差 $\small \varphi$ $\small \varepsilon t$ 加速度误差 $\small \Delta \alpha$ $\small \delta$ 加速度误差 $\small \Delta \alpha$ $\small g\sin\varphi=g\varphi=g\varepsilon t$ 速度误差 $\small \Delta v$ $\small \int \delta\, \mathrm{d}t=\delta t$ 速度误差 $\small \Delta v$ $\small \int g\varepsilon t\, \mathrm{d}t=\frac{1}{2}g\varepsilon t^2$ 位置误差 $\small \Delta x$ $\small \int \delta t\, \mathrm{d}t=\frac{1}{2}\delta t^2$ 位置误差 $\small \Delta x$ $\small \int \frac{1}{2}g\varepsilon t^2\, \mathrm{d}t=\frac{1}{6}g\varepsilon t^3$

由此可见加速度计零偏所引起的载体位置误差量级为时间的二次方，而陀螺仪漂移相应则为时间的三次方；故后者对惯性导航精度的影响大于前者。

6.矢量叉乘的矩阵形式

矢量叉乘为矢量基本运算之一，遵循右手定则。我们熟知的向量叉乘往往是行列式形式，设第一个运算数为 $\small \boldsymbol{r}=\left ( r_x,r_y,r_z \right )^T$ ，第二个运算数为 $\small \boldsymbol{s}=\left ( s_x,s_y,s_z \right )^T$ ，则有如下运算结果：

$\small \boldsymbol{r}\times\boldsymbol{s}=\left ( r_x,r_y,r_z \right )^T\times\left ( s_x,s_y,s_z \right )^T=\begin{pmatrix} \begin{vmatrix} r_y&r_z \\ s_y&s_z \end{vmatrix}, &\begin{vmatrix} r_z&r_x \\ s_z&s_x \end{vmatrix}, & \begin{vmatrix} r_x&r_y \\ s_x&s_y \end{vmatrix} \end{pmatrix}^T$

在惯性导航的各类方程推算中，矢量的叉乘常使用矩阵形式，设矢量 $\small \boldsymbol{t}=\left ( t_x,t_y,t_z \right )^T=\boldsymbol{r}\times\boldsymbol{s}$ ，则有下式成立

$\small \begin{bmatrix} t_x\\t_y \\t_z \end{bmatrix}=\begin{bmatrix} 0 &-r_z &r_y \\ r_z &0 &-r_x \\ -r_y &r_x &0 \end{bmatrix}\begin{bmatrix} s_x\\s_y \\ s_z \end{bmatrix}$

二、指北方位惯导系统力学编排 1.平台指令角速度

指北方位系统以地理坐标系为导航坐标系，即理想平台坐标系 $\small T$ 应当跟踪地理坐标系 $\small g$ ，将三个加速度计的敏感轴定向在运载体当地的东、北、天方位上。

$\small \boldsymbol{\omega}_{iT}=\boldsymbol{\omega}_{ig}$

而地理坐标系的旋转角速度 $\small \boldsymbol{\omega}_{ig}$ 由两部分组成，其一为地球旋转角速度 $\small \boldsymbol{\omega}_{ie}$ ，其二为由运载体运动引起的相对地球的旋转角速度 $\small \boldsymbol{\omega}_{eg}$ 。

$\small \boldsymbol{\omega}_{ig}=\boldsymbol{\omega}_{ie}+\boldsymbol{\omega}_{eg}$

首先看第一项，由于理想平台坐标系 $\small T$ 应当跟踪地理坐标系 $\small g$ ，故以地理坐标系为视角，只需将地球旋转角速度 $\small \boldsymbol{\omega}_{ie}$ 沿地理坐标系的各轴进行分解。请看《惯性导航》中的下图

地球旋转角速度 $\small \boldsymbol{\omega}_{ie}$ 可在地理坐标系的北、天方向进行分解，有

$\small \boldsymbol{\omega}_{ie}^g=\begin{bmatrix} 0\\ \omega_{ie}\cos L\\ \omega_{ie}\sin L \end{bmatrix}$

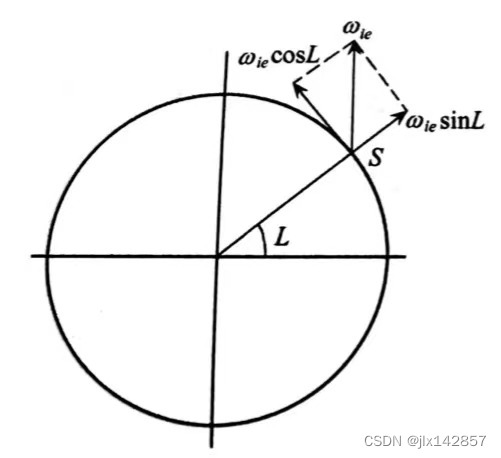
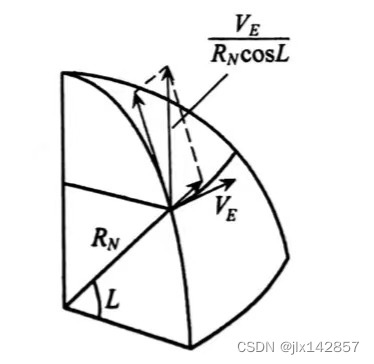
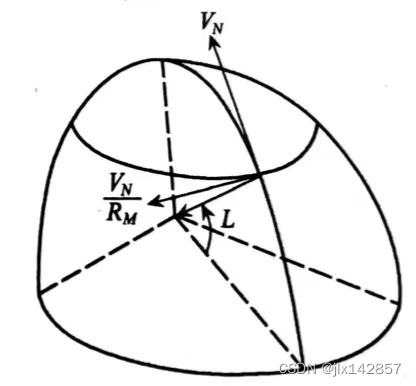
对于由运载体运动引起的相对地球的旋转角速度 $\small \boldsymbol{\omega}_{eg}$ ，首先看运载体的北向速度引起的角速度分量，请看下图

载体的北向速度 $\small V_N$ 引起其相对地球的西向角速度，设 $\small R_M$ 为当地经度圈的半径，则产生东向角速度分量为 $\small -\frac{V_N}{R_M}$ ；

其次，看运载体的东向速度 $\small V_E$ 引起的角速度分量，请看下图

该东向速度沿当地纬度圈，故产生一沿地球旋转轴的角速度分量（与 $\small \boldsymbol{\omega}_{ie}$ 一致），设当地极轴长度为 $\small R_N$ ，则纬度圈半径为 $\small R_N\cos L$ ；同样可将该角速度分解为地理坐标系中的北、天方向，分别乘 $\small \cos L$ 和 $\small \sin L$ 。综上可得 $\small \boldsymbol{\omega}_{eg}$ 沿东、北、天方向的分量如下

$\small \boldsymbol{\omega}_{eg}^g=\begin{bmatrix} -\frac{V_N}{R_M}\\ \frac{V_E}{R_N\cos L}\cos L\\ \frac{V_E}{R_N\cos L}\sin L \end{bmatrix}=\begin{bmatrix} -\frac{V_N}{R_M}\\ \frac{V_E}{R_N}\\ \frac{V_E}{R_N}\tan L \end{bmatrix}$

事实上，请让我们感性地比较地球旋转角速度 $\small \boldsymbol{\omega}_{ie}$ 与由运载体运动引起的相对地球的旋转角速度 $\small \boldsymbol{\omega}_{eg}$ ，事实上 $\small \boldsymbol{\omega}_{eg}$ 中的 $\small \frac{V_E}{R}$ ，可近似想象为“飞机速度/地球半径”，进一步想象为“1马赫(音速)/6000多公里”，相较于地球旋转角速度可以说是十分渺小了；故在一些精度要求不高的惯性导航系统中，该项甚至可以忽略不计。

综合两种角速度的表达式，得到目标为跟踪地理坐标系的平台指令角速度如下

$\small \begin{bmatrix} \boldsymbol{\omega}_{\textup{cmd}x}\\ \boldsymbol{\omega}_{\textup{cmd}y}\\ \boldsymbol{\omega}_{\textup{cmd}z} \end{bmatrix}=\boldsymbol{\omega}_{iT}^T=\boldsymbol{\omega}_{ig}^g=\boldsymbol{\omega}_{ie}^g+\boldsymbol{\omega}_{eg}^g=\begin{bmatrix} -\frac{V_N}{R_M}\\ \omega_{ie}\cos L+\frac{V_E}{R_N}\\ \omega_{ie}\sin L+\frac{V_E}{R_N}\tan L \end{bmatrix}$

2.速度方程

关于速度方程的推导，其思路比较直接，将上节所求的角速度代入先前求得的比力方程即可；由于飞机速度 $\small V$ 为地速，故在地理坐标系下进行推导。

$\small \dot{\boldsymbol{V}}=\boldsymbol{f}-\left ( 2\boldsymbol{\omega}_{ie}+\boldsymbol{\omega}_{eg} \right )\times\boldsymbol{V}+\boldsymbol{g}$

将向量及叉乘运算写成矩阵形式，即

$\tiny \begin{bmatrix} \dot{V}_E\\ \dot{V}_N\\ \dot{V}_U \end{bmatrix}=\begin{bmatrix} f_E\\ f_N\\ f_U \end{bmatrix}-\begin{bmatrix} 0 &-\left (2\omega_{iez}+\omega_{egz} \right ) &\left (2\omega_{iey}+\omega_{egy} \right ) \\ \left (2\omega_{iez}+\omega_{egz} \right )&0 &-\left (2\omega_{iex}+\omega_{egx} \right ) \\ -\left (2\omega_{iey}+\omega_{egy} \right ) &\left (2\omega_{iex}+\omega_{egx} \right ) &0 \end{bmatrix}\begin{bmatrix} V_E\\V_N \\ V_U \end{bmatrix}+\begin{bmatrix} 0\\ 0\\ g \end{bmatrix}$