5.3.1 (2) 函数的单调性(含参函数) |
您所在的位置:网站首页 › 怎样求函数的单调递增区间 › 5.3.1 (2) 函数的单调性(含参函数) |
5.3.1 (2) 函数的单调性(含参函数)
|
\({\color{Red}{欢迎到学科网下载资料学习 }}\) [ 【基础过关系列】高二数学同步精品讲义与分层练习(人教A版2019)] ( https://www.zxxk.com/docpack/2875423.html) \({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\) 选择性第二册同步巩固,难度2颗星! 基础知识 函数单调性与导数在某个区间\((a ,b)\)内,若\(f'(x)>0\),则函数\(y=f(x)\)在这个区间内单调递增;
若\(f'(x)0\)时,不能想当然:\(x> \dfrac{1}{a}\);要分\(a=0\),\(a>0\),\(a0\)时
\(a0\),\(f(x)\)在\(R\)上为增函数,
(2)若\(k≠0\)时,则由\(kx+1=0\)得\(x=- \dfrac{1}{k}\) (需要对\(y=kx+1\)的斜率正负讨论)
① 若\(k>0\)时,
当\(x0\),\(f(x)\)递增;
【典题1】 求函数\(f(x)=\dfrac{x^3}{3}-\dfrac{a+2}{2} x^2+2 a x+1\)的单调性. 解析 \(f'(x)=x^2-(a+2)x+2a=(x-2)(x-a)\), (求导后因式分解,确定导函数是否存在零点,若有,是多少,有几个?) (1)若\(a=2\)时,\(f(x)\)在\(R\)上递增; 
(2)若\(a>2\)时,
当\(00\); \(\therefore f(x)\)在\((0,2)\)上为减函数,在\((2,+∞)\)上为增函数 ② 若\(a>0\),则\(∆=1+8a>0\), 由\(ax^2+x-2=0\)得\(x_1=\dfrac{-1-\sqrt{1+8 a}}{2 a}0\), (作出 \(g(x)=ax^2+x-2\)的图像,由图像可知) 
\(f(x)\)在\((0,x_2)\)上为减函数,在\((x_2,+∞)\)上为增函数.
综上所述:
\(a=0\)时,\(f(x)\)在\((0,2)\)上为减函数,在\((2,+∞)\)上为增函数
\(a>0\)时,\(f(x)\)在\(\left(0, \dfrac{-1+\sqrt{1+8 a}}{2 a}\right)\)上为减函数,在\(\left(\dfrac{-1+\sqrt{1+8 a}}{2 a},+\infty\right)\)上为增函数.
点拨 对于导函数\(f'(x)=ax^2+bx+c\)中二次项系数\(a\)不确定,要分\(a=0\),\(a>0\),\(ax_1\),
当\(x_10\),\(f(x)\)递增.
综上所述,当\(-20\),故\(f(x)\)在\((0,+∞)\)单调递增;
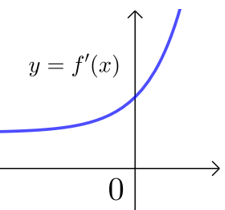
(2)若\(a0\),\(f(x)\)递增;
当\(x0\),\(f(x)\)在\((-∞,+∞)\)上单调递增;
当\(a0\)
当\(x0\);
(2)若\(a0\),\(f(x)\)递增.
③若\(a-1⇒x_1>x_2\),
当\(-10\),\(f(x)\)递增.
综上,
当\(a≥0\)时,\(f(x)\)在\((-∞,-1)\)递减,在\((-1,+∞)\)递增,
当\(-\dfrac{1}{e}0\),此时函数\(f(x)\)为增函数,
当\(x∈[1,+∞)\)时,\(f'(x)0\),此时函数\(f(x)\)为增函数.
综上所述:
若\(a=0\),函数不具有单调性;
若\(a>0\),函数\(f(x)\)在\((0,1)\)上单调递增,在\([1,+∞)\)上单调递减;
若\(a0\),\(f(x)\)在\((0,+∞)\)上递增;
(2)当\(a \neq 0\)时,
①若\(a>0\),\(f'(x)>0\),\(f(x)\)在\((0,+∞)\)上递增;
②若\(a0\),\(f(x)\)单调递增,
在\((1,\ln a)\)上,\(f'(x)0\)
当\(x0\);
(2)若\(a0\),\(f(x)\)递增.
③若\(a-1⇒x_1>x_2\),
当\(-10\),\(f(x)\)递增.
综上,
当\(a≥0\)时,\(f(x)\)在\((-∞,-1)\)递减,在\((-1,+∞)\)递增,
当\(-\dfrac{1}{e}2\)时,
|
【本文地址】
今日新闻 |
推荐新闻 |
 ② 当\(k0\),函数单调递增,
\(x \in\left(-\infty, \dfrac{1}{m}-1\right)\)时,\(f'(x)0\),函数单调递增.
情况2 二次函数型
② 当\(k0\),函数单调递增,
\(x \in\left(-\infty, \dfrac{1}{m}-1\right)\)时,\(f'(x)0\),函数单调递增.
情况2 二次函数型
 当\(20\),\(f(x)\)递增;
(3)若\(a0\),\(f(x)\)递增.
点拨 导函数\(f'(x)=(x-a)(x-b)\)有零点,要分\(a=b\),\(a>0\),\(a0)\),
令\(g(x)=ax^2+x-2\)(这不一定是二次函数,需要讨论函数类型)
① 若\(a=0\),\(g(x)=x-2\),
当\(20\),\(f(x)\)递增;
(3)若\(a0\),\(f(x)\)递增.
点拨 导函数\(f'(x)=(x-a)(x-b)\)有零点,要分\(a=b\),\(a>0\),\(a0)\),
令\(g(x)=ax^2+x-2\)(这不一定是二次函数,需要讨论函数类型)
① 若\(a=0\),\(g(x)=x-2\),

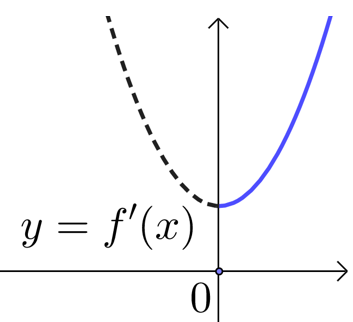 ②若\(00\); \(x \in\left(\sqrt{\dfrac{p}{2(1-p)}},+\infty\right)\)时,\(f'(x)0\),\(f(x)\)在\(R\)上递增;
②若\(00\); \(x \in\left(\sqrt{\dfrac{p}{2(1-p)}},+\infty\right)\)时,\(f'(x)0\),\(f(x)\)在\(R\)上递增; 当\(00\)讨论.)
①当\(a≤1\)时,\(p(x)≥p(0)=1-a≥0\),即\(g'(x)≥0\),
故\(g(x)\)在\([0,+∞)\)上单调递增;
当\(00\)讨论.)
①当\(a≤1\)时,\(p(x)≥p(0)=1-a≥0\),即\(g'(x)≥0\),
故\(g(x)\)在\([0,+∞)\)上单调递增;
 ②当\(a>1\)时,\(p(0)=1-a0\)时,\(y=f'(x)\)在\((-∞,\ln a)\)是减函数,在\((\ln a,+∞)\)上是增函数.
(2)略.
解析 (1)由已知\(f'(x)=e^x-ax-1\),
设\(g(x)=f'(x)=e^x-ax-1\),则\(g'(x)=e^x-a\),
①当\(a≤0\)时,\(g'(x)=e^x-a>0\)在\(R\)上恒成立,
所以\(g(x)=f'(x)=e^x-a>0\)在\(R\)上恒成立,
所以\(g(x)=f'(x)\)在\((-∞,+∞)\)上单调递增,
②当\(a>0\)时,令\(g'(x)>0\)得\(x>\ln a\),\(g'(x)0\)时,\(y=f'(x)\)在\((-∞,\ln a)\)是减函数,在\((\ln a,+∞)\)上是增函数.
(2)由(1)知,①当\(a≤0\)时,\(f'(x)=e^x-ax-1\)在\((-1,+∞)\)上单调递增,
又\(f'(0)=0\),
所以\(-10\),
则\(f(x)\)在\((-1,0)\)上单调递减,在\((0,+∞)\)上单调递增,
所以 \(f(x)_{\min }=f(0)=1\),
②当\(0
②当\(a>1\)时,\(p(0)=1-a0\)时,\(y=f'(x)\)在\((-∞,\ln a)\)是减函数,在\((\ln a,+∞)\)上是增函数.
(2)略.
解析 (1)由已知\(f'(x)=e^x-ax-1\),
设\(g(x)=f'(x)=e^x-ax-1\),则\(g'(x)=e^x-a\),
①当\(a≤0\)时,\(g'(x)=e^x-a>0\)在\(R\)上恒成立,
所以\(g(x)=f'(x)=e^x-a>0\)在\(R\)上恒成立,
所以\(g(x)=f'(x)\)在\((-∞,+∞)\)上单调递增,
②当\(a>0\)时,令\(g'(x)>0\)得\(x>\ln a\),\(g'(x)0\)时,\(y=f'(x)\)在\((-∞,\ln a)\)是减函数,在\((\ln a,+∞)\)上是增函数.
(2)由(1)知,①当\(a≤0\)时,\(f'(x)=e^x-ax-1\)在\((-1,+∞)\)上单调递增,
又\(f'(0)=0\),
所以\(-10\),
则\(f(x)\)在\((-1,0)\)上单调递减,在\((0,+∞)\)上单调递增,
所以 \(f(x)_{\min }=f(0)=1\),
②当\(0