python数据分析及可视化(二)离散程度、标准化值、分布形态、描述性统计图表 |
您所在的位置:网站首页 › 平均数是一组数据什么水平的 › python数据分析及可视化(二)离散程度、标准化值、分布形态、描述性统计图表 |
python数据分析及可视化(二)离散程度、标准化值、分布形态、描述性统计图表
|
描述性统计
平均指标
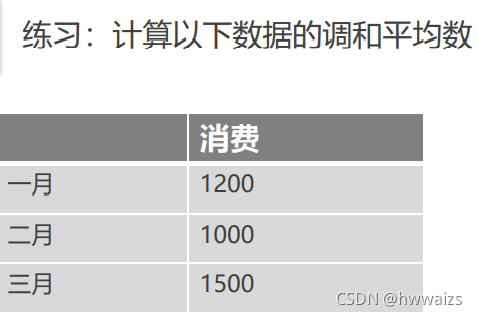
调和平均数
算术平均数的变种,本质跟算术平均数是一致的。 定义:变量值倒数的算术平均值的倒数。表示的符号:
H
H
H 调和平均数(根据未分组数据计算的):
H
=
n
1
x
1
+
1
x
2
+
.
.
.
+
1
x
n
H=\frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+...+\frac{1}{x_n}}
H=x11+x21+...+xn1n 注意: • 所有数据需大于0 • 容易受到异常值的影响 倒数本身就是伪装的乘法,倒数可以更加便捷的帮助除以分数。 5/(3/7) = 5*(7/3) = 35/3 5/(3/7) = (5/1)/(3/7) = (35/7)/(3/7) = 35/3 调和平均数可以帮助我们能在不担心共同分母的情况下找到对应的乘/除关系。所以,调和平均数有助于处理周期不同的比率的数据集。 例题:某人去超市买东西,路程s = 5 miles,去时速度v = 30 mph,返回时速度v = 10 mph,求整个行程的平均速度。 解法1: 加权平均数 = V 1 ∗ 去程所花时间的权重 + V 2 ∗ 返程所花时间的权重 加权平均数 = V_1*去程所花时间的权重 + V_2*返程所花时间的权重 加权平均数=V1∗去程所花时间的权重+V2∗返程所花时间的权重 去程所花的时间 s = v ∗ t s = v*t s=v∗t,除以60是进行时间单位的换算 t 1 t_1 t1 = 5/(30/60) = 10 min返程所花的时间 t 2 t_2 t2 = 5/(10/60) = 30 min计算加权平均数,总时间 t = t 1 + t 2 t = t_1+t_2 t=t1+t2 v v v = (30*(10/40)) + (10*(30/40)) = 15解法2:调和平均数计算,适用于周期不同的数据。 v v v = 2/((1/30)+(1/10)) = 15 均值不等式对于同一组数据,一定满足: 算术平均数 ≥ 几何平均数 ≥ 调和平均数 算术平均数\geq几何平均数\geq调和平均数 算术平均数≥几何平均数≥调和平均数 当所有数据取值相同的时候,等号成立。算术平均数和几何平均数都受较大值的影响较大,算术平均数影响更大;调和平均数受到最小值的影响较大。 几种平均数的用法: 数据呈现直线,使用算术平均数周期一致,数据呈现乘数级或指数级增长的时候,使用几何平均数周期不一致,量级也不一致,呈现乘数级或指数级增长,使用调和平均数 离散程度描述反映各变量值远离其中心值得程度,是数据分布的另一个重要特征。观察数据时看数据主要分布在哪一块,异常点在哪,根据数据去除异常值,要观察离散程度,单一的、集中的指标不足以衡量的,二者结合才能证明数据是集中性比较强的。 主要衡量指标: 1.极差 2.平均差 3.标准差 4.变异系数 极差一组数据的最大值与最小值之差。表示的符号为: R R R,计算公式为: R = m a x ( x ) − m i n ( x ) R = max(x) - min(x) R=max(x)−min(x)。 如:A:100 800 900 1000 1100 1200 3000;B:100 200 300 400 500 600 3000。 A和B 的极差均为 3000-100 = 2900,单看极差值可以看到A和B的离散程度是相同的,其实并不是。 特点:离散程度的最简单测度值;极易受极端值影响;未考虑数据的分布。因此,我们很少用它来衡量数据的离散程度。 平均差(离差)各变量值与其均值差绝对值的平均数。表示的符号为:
M
d
M_d
Md, 计算公式为:
M
d
=
∑
i
=
1
n
∣
x
i
−
x
ˉ
∣
n
M_d=\frac{\sum_{i=1}^n|x_i-\bar{x}|}{n}
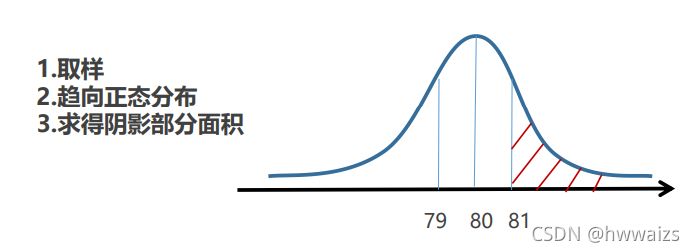
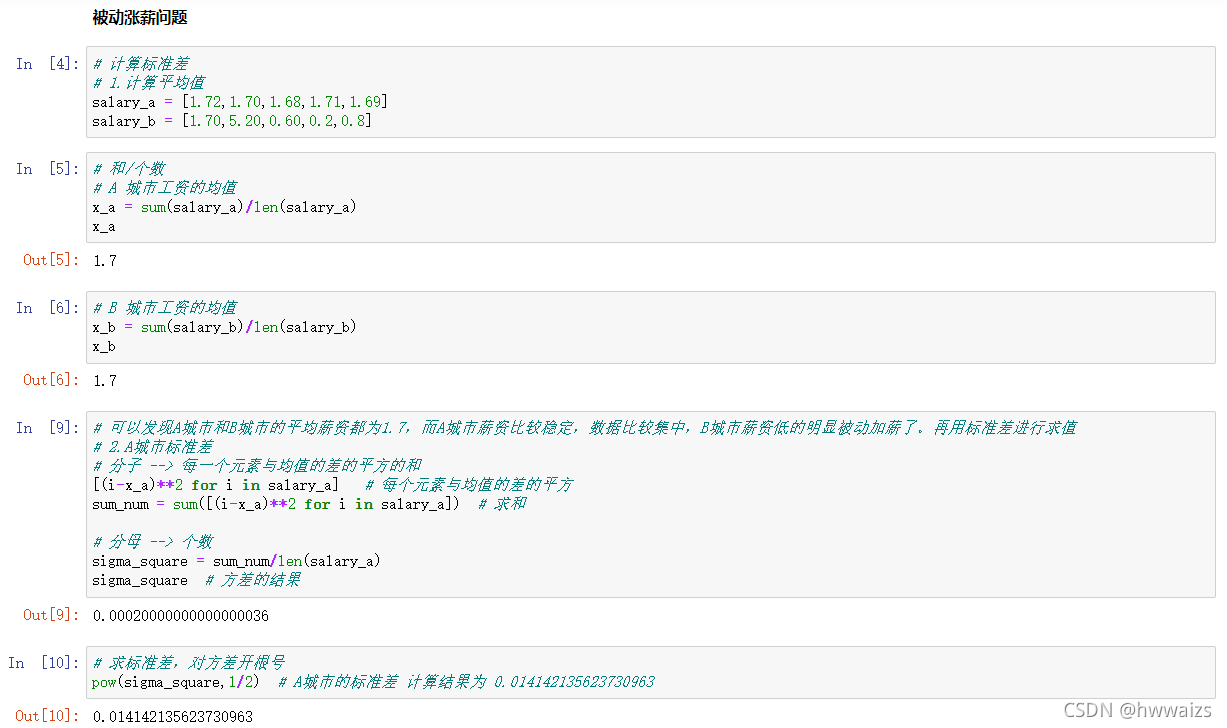
Md=n∑i=1n∣xi−xˉ∣ 例题:计算3 6 6 7 8 11 15 16 的平均差 数据相加后除以数据的个数8,求得数据的平均值为9,然后求每个数距离9的差值的绝对值(即3-9,6-9等等的绝对值),相加除以数据的个数8,就得平均差为3.75 特点: • 能全面反映一组数据的离散程度。平均差越大,数据离均值越远,也就是越分散;平均差越小,数据离均值越近,表明数据越集中。 • 数学性质较差,对绝对值求导不易计算,实际应用较少。 可以用方差解决此类问题,对数据进行平方进行计算。 方差和标准差总体方差定义:变量值与其算术平均数的离差的平方的算术平均数。 总体方差表示符号: σ 2 \sigma^2 σ2 总体方差公式: σ 2 = ∑ i = 1 N ( x i − μ ) 2 N \sigma^2=\frac{\sum_{i=1}^N(x_i-\mu)^2}{N} σ2=N∑i=1N(xi−μ)2, μ \mu μ表示均值 为了解决计算量的问题,我们使用标准差: 总体标准差表示符号: σ \sigma σ 总体标准差公式: σ = ∑ i = 1 N ( x i − μ ) 2 N = σ 2 \sigma=\sqrt{\frac{\sum_{i=1}^N(x_i-\mu)^2}{N}}=\sqrt{\sigma^2} σ=N∑i=1N(xi−μ)2 =σ2 特点: • 数据离散程度最常用的测度值,最常用的衡量数据离散程度的指标 • 反映了各变量值与均值的平均差异,标准差越大,数据离平均值的差异越大,数据就越离散;标准差越小,数据离平均值的差异就越小,数据就越集中。 例题1:针对被动涨薪的问题,深入剖析,数据单位为万元。 A市薪资:[1.72,1.70,1.68,1.71,1.69] B市薪资:[1.70,5.20,0.60,0.2,0.8] 变异系数(离散系数)是标准差与均值之比,符号位 V s V_s Vs。 计算公式为: V s = S x ˉ V_s=\frac{S}{\bar{x}} Vs=xˉS 特点: • 是对数据相对离散程度的测度 • 消除了数据水平不同和数据计量单位不同对数据离散程度的影响 • 常用于对不同组别数据离散程度的比较 集中型数据衡量的指标是均值,离散型数据衡量的指标是标准差,可以使用均值和标准差来实现标准化值。 导入分析中国人寿命超过81岁的概率,已知如下:均值为80,标准差为0.5。 先进行取样,只要基数够大,都会趋向于正态分布,可以使用样本去推整体。根据条件绘制出概率密度曲线如上图所示,对于概率密度曲线来说,面积表示的是概率,所以超过81岁人的概率就转化为求出81岁右边曲线内的面积。直接用积分求面积会很复杂,可以利用标准化求解。 标准化作用:标准化将服从正态分布的数据集变为了均值为0,标准差为1的标准正态分布。 表示符号: Z i Z_i Zi 公式: Z i = x i − x ˉ S Z_i = \frac{x_i-\bar{x}}{S} Zi=Sxi−xˉ 很多情况下,只要数据服从正态分布,我们都会将其转化为标准正态分布,假设我们求的是标准正态分布中 |
【本文地址】
今日新闻 |
推荐新闻 |
 H
=
n
1
x
1
+
1
x
2
+
.
.
.
+
1
x
n
=
(
120
0
−
1
+
100
0
−
1
+
150
0
−
1
3
)
−
1
=
3
1
1200
+
1
1000
+
1
1500
H = \frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+...+\frac{1}{x_n}} = (\frac{1200^{-1}+1000^{-1}+1500^{-1}}{3})^{-1} = \frac{3}{\frac{1}{1200}+\frac{1}{1000}+\frac{1}{1500}}
H=x11+x21+...+xn1n=(31200−1+1000−1+1500−1)−1=12001+10001+150013
H
=
n
1
x
1
+
1
x
2
+
.
.
.
+
1
x
n
=
(
120
0
−
1
+
100
0
−
1
+
150
0
−
1
3
)
−
1
=
3
1
1200
+
1
1000
+
1
1500
H = \frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+...+\frac{1}{x_n}} = (\frac{1200^{-1}+1000^{-1}+1500^{-1}}{3})^{-1} = \frac{3}{\frac{1}{1200}+\frac{1}{1000}+\frac{1}{1500}}
H=x11+x21+...+xn1n=(31200−1+1000−1+1500−1)−1=12001+10001+150013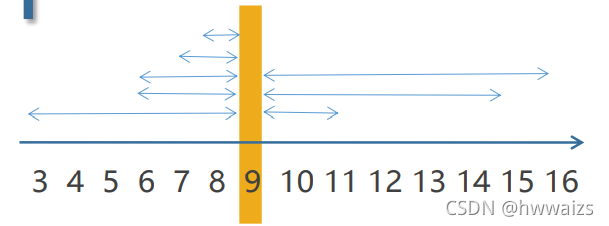
 例题2:如果把A城市的薪资单位改为元呢?数据如[17200.0, 17000.0, 16800.0, 17100.0, 16900]
例题2:如果把A城市的薪资单位改为元呢?数据如[17200.0, 17000.0, 16800.0, 17100.0, 16900] 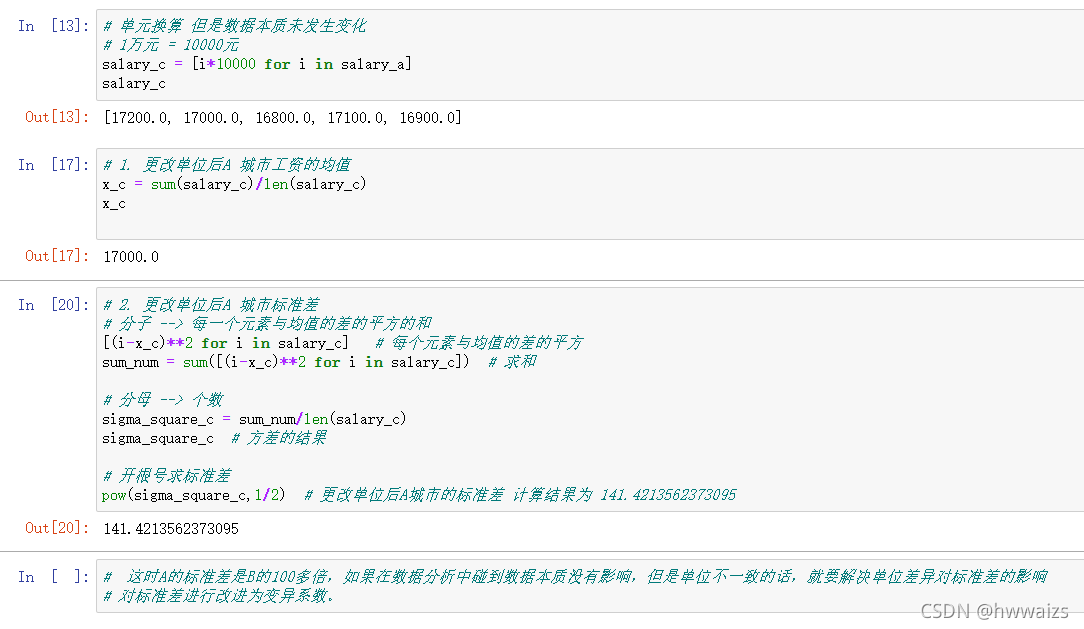
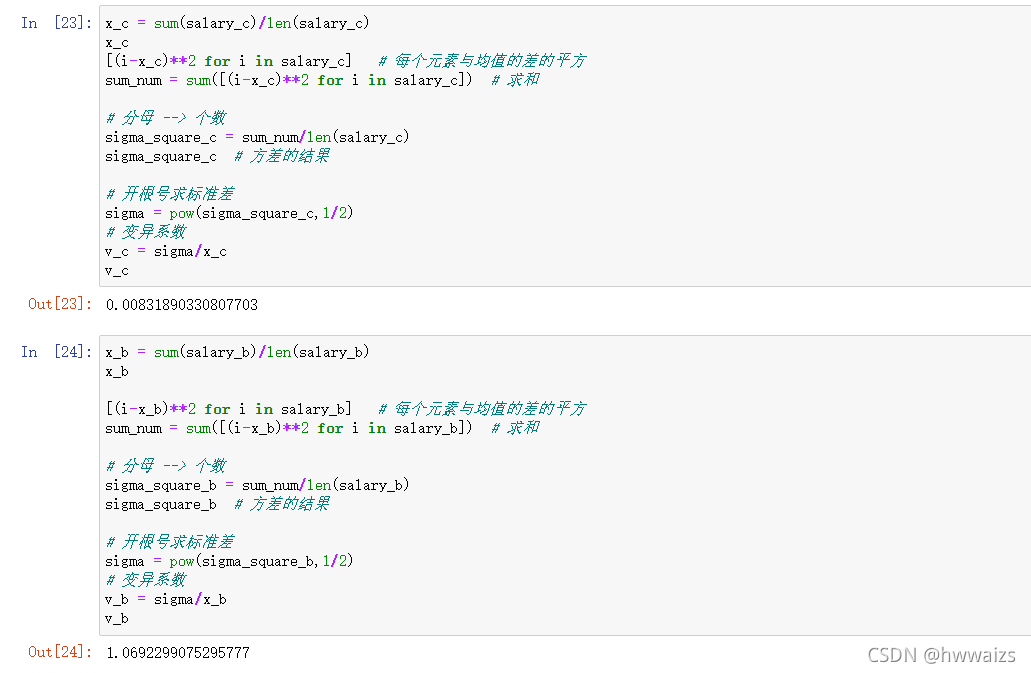 B城市薪资的变异系数为A城市的100多倍,剔除了单位对数据的影响。
B城市薪资的变异系数为A城市的100多倍,剔除了单位对数据的影响。