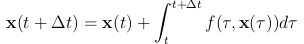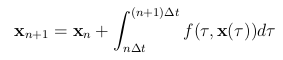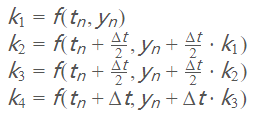设F(x)为函数f(x)的一个原函数，我们把函数f(x)的所有原函数F(x)+C（C为任意常数）叫做函数f(x)的不定积分(indefinite integral)。

非线性微分方程:

在有限的时间间隔Δt积分:

连续时间内积分:

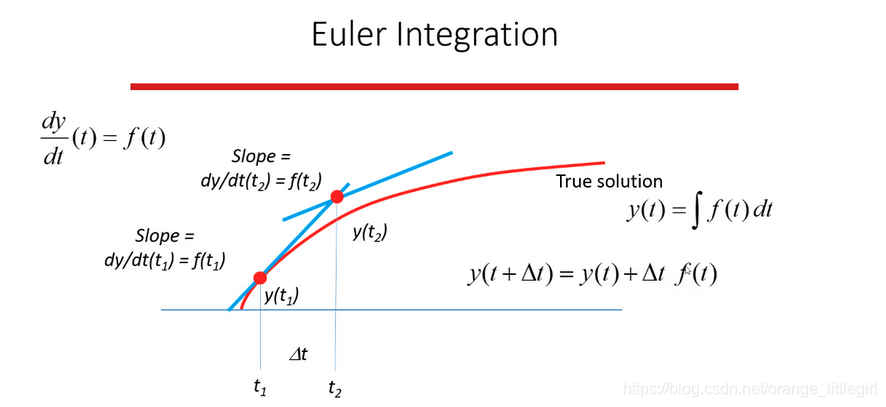
工程上最常见的有三种：欧拉积分（Euler method）、中值积分（Midpoint method）和龙格－库塔法积分（Runge–Kutta methods）。他们的区别就是如何用数值方法模拟一个斜率。这里简单总结如下：

设有如下微分方程：

欧拉方法假设导数在区间内是恒定的，作为一般的RK方法，这对应于单阶段方法，计算初始点的导数，并用它来计算终点的积分值

中值积分法假设导数是间隔中点的导数，并进行一次迭代来计算此中点的fx值。

设有如下微分方程：

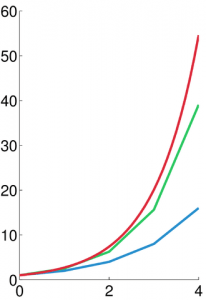
欧拉积分与中值积分都是一阶近似并没有本质不同，二者只是一阶导数所取位置不同，他们的性能也有差别，如下图所示，作为一阶积分近似方法来讲，中点积分有时会稍好一些（带来更快的收敛速度）。

龙格－库塔法（Runge-Kutta methods）是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。在工程中最常用的是 四阶龙格－库塔积分，也就是 RK4 积分，它的计算方式如下：

设有如下微分方程：

其中：

k1 是时间段开始时的斜率；k2 是时间段中点的斜率，通过欧拉法采用斜率k1来决定y在点tn + h/2的值；k3 也是中点的斜率，但是这次采用斜率k2决定y值；k4 是时间段终点的斜率，其y值用k3决定。 其数学公式如下：

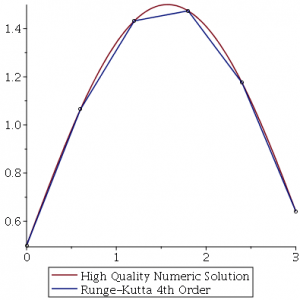
从公式中可以看出两个中点的斜率具有更大的权重。龙格－库塔法的示意图如下，它也是一种更高阶的逼近方法，通常也具有更好的逼近效果，总累计误差为 Δt4 阶。

Runge-Kutta4假定评估值，对于 f()​在间隔的开始，中点，中点的中点和结束。它使用四个阶段迭代计算积分，用四个导数k 1~k 4，顺序获得。然后对这些导数进行加权平均，以获得4阶估计值间隔中的导数。 RK4方法更好地指定为一个小算法而不是一步式公式。

龙格-库塔方法的推导基于Taylor展开方法，因而它要求所求的解具有较好的光滑性。如果解的光滑性差，那么，使用四阶龙格-库塔方法求得的数值解，其精度可能反而不如改进的欧拉方法。在实际计算时，应正对问题的具体特点选择适合的算法。对于光滑性不太好的解，最好采用低阶算法而将步长取小。