概论 |
您所在的位置:网站首页 › 已知概率密度和期望求常数ab › 概论 |
概论
|
一. 定义
1. 一维离散型随机变量的期望
定义2:设连续型随机变量 X的概率密度为f(x), 若积分 注意: 被积函数是: xf(x) 容易得出,连续型求期望E(X),极可能用到定积分的分部积分法!!再次强调此法: 看例题:
几种重要分布的数学期望参考 概率论_第4章__几种重要的随机变量的分布及其数字特征的表 3. 一维随机变量函数的期望

5. 二维随机变量函数, 求期望是这样做:
对于二维离散型随机变量, 先求分布律再按定义求数学期望, 要比直接使用上面公式简单。 其他情况都直接采用公式而不计算新的分布律、密度函数。 二 期望的性质以下公式中C为常数, X、Y为随机变量 1. E(C) = C 2. E(CX) = C·E(X) 3. E(X+Y) = E(X) + E(Y), 上述可以推广为多个随机变量相加; 可以推广: E(C₁X+C₂Y) = C₁E(X)+C₂E(Y), 其中 C₁, C₂为常数 4. 若X, Y是相互独立的随机变量,则 E(XY) = E(X)E(Y). 此公式可以推广: 任意有限个独立的随机变量 相乘。 三 光说不练是假把式,看例题 题1一银行服务需要等待, 设等待时间X (以分钟计) 服从期望为 10 的指数分布, 某人进了银行, 且打算过会去办另一件事, 于是先等待, 如果超过15分钟还没有等到服务就离开,设他实际的等待时间为 Y, 求此人实际等待的平均时间 E(Y). 解 由题意知,Y = min{X, 15}, 设 g(x) = min{x, 15}, 则 Y=g(X), 根据 连续型随机变量函数的期望的定义:
又因为:
设X的概率密度为 解: 注意: 本题需要 求一个期望值,随机变量是一个绝对值,我们先求出E(X), 要明白X- 在计算时可以看成 x- , 有的人看到 X-就慌了, X- 应该怎样处理呀? 实际只要看成 x- 就行了。 因为密度函数是一个分段函数, 求期望E(X) 要分段计算,再求和。 解题过程如下 E[|X-E(X)|] = E[|X-1|] = ~~~~~~ 四 随机变量的期望不是必然存在,因为求期望是通过求无穷级数或广义积分, 就存在是否收敛的问题。只有无穷级数 或者广义积分 收敛, 期望才存在。 看一个例题
|
【本文地址】
今日新闻 |
推荐新闻 |

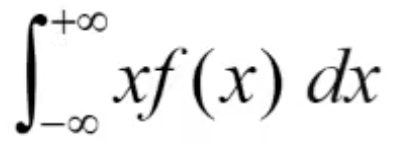 绝对收敛, 称其为X的数学期望。记为:
绝对收敛, 称其为X的数学期望。记为: 
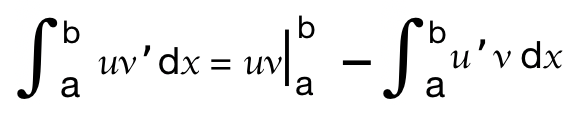
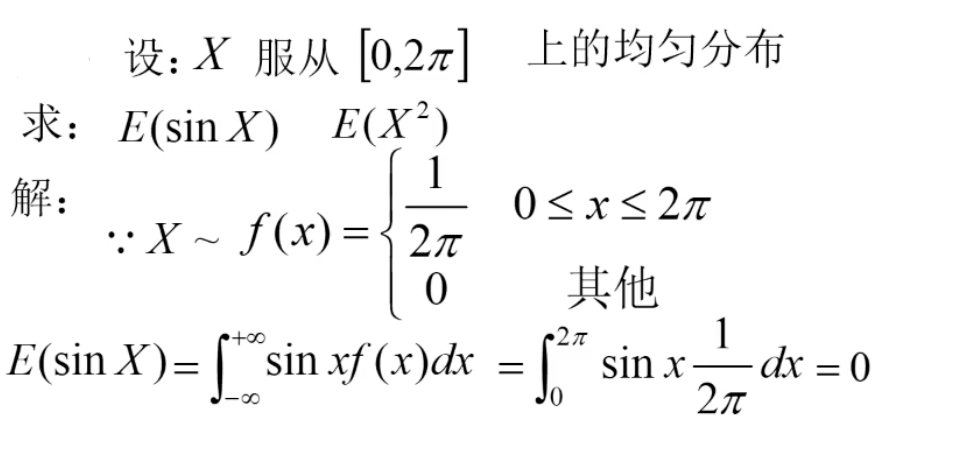
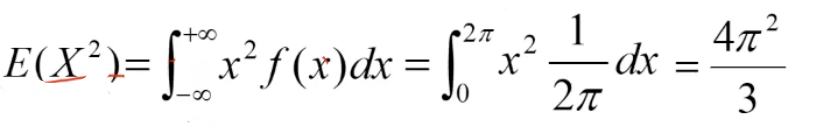

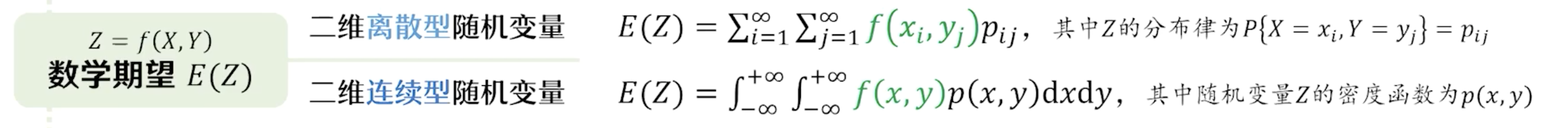
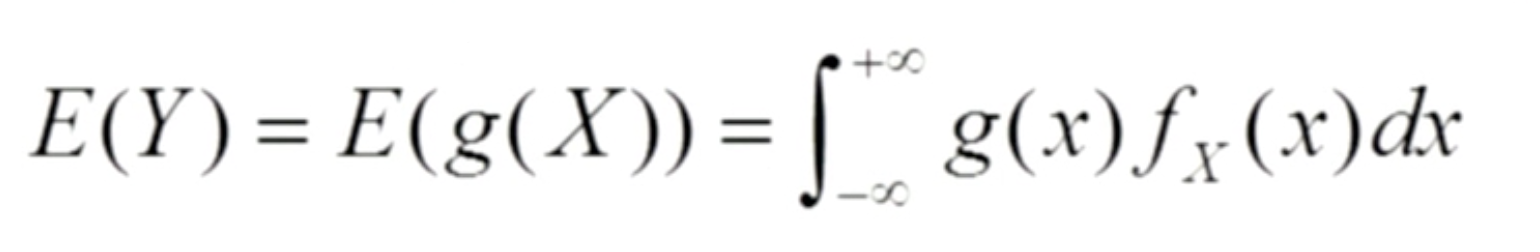
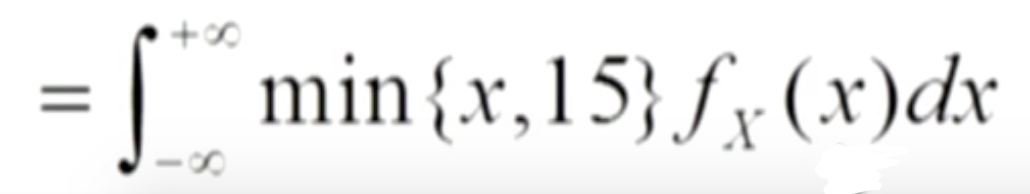
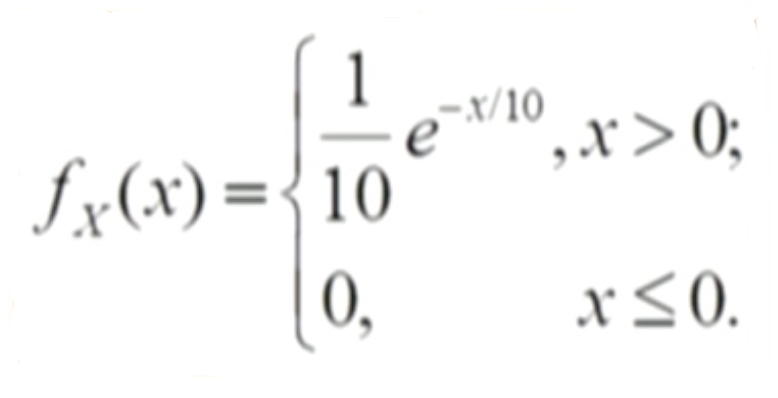

 , 求E[ |X-E(X)| ].
, 求E[ |X-E(X)| ].