小波分析 |
您所在的位置:网站首页 › 小波的邀请码 › 小波分析 |
小波分析
|
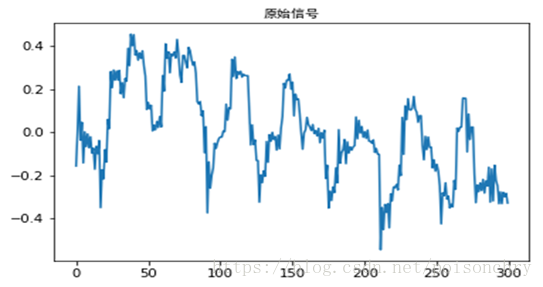
我们知道频域滤波函数的一个特点,就是可以从原始数据中找出和积函数关联性相关性更高的成分。根据小波函数的特点,它也具备和这类函数相似的特点,而且比固定尺寸和卷积,或者需要依靠滑动窗口分析的傅立叶要更灵活。 事实上,自从小波分析被提出后,已经在很多地方广泛使用,并且在一定程度上取代了傅立叶分析。在这一章节里,我将为大家介绍这种神奇的小波分析。 小波变化/小波分析 (Wavelet Transform)首先,有请小波函数: C W T x ψ ( τ , s ) = Ψ x ψ ( τ , s ) = 1 ∣ s ∣ ∫ f ( t ) ⋅ ψ ∗ ( t − τ s ) d t CWT_{x}^{\psi}(\tau, s) = \Psi_{x}^{\psi}(\tau, s) = \frac{1}{\sqrt{|s|}} \int f(t) \cdot \psi^*(\frac{t - \tau}{s}) dt CWTxψ(τ,s)=Ψxψ(τ,s)=∣s∣ 1∫f(t)⋅ψ∗(st−τ)dt 从小波核函数的形式 ψ ∗ ( t − τ s ) \psi^*(\frac{t - \tau}{s}) ψ∗(st−τ)可知: 它通过 1 / s 1/s 1/s控制了函数的缩放, s s s越大,小波核的频率越低,反之则越高;它通过 τ \tau τ进行了平滑位移。如果对此还难以想象,那么我们其实可以构建这样一个函数: f ( x ) = e − x 2 f(x) = e^{-x^2} f(x)=e−x2 它的函数图如下:
如果对它做一下位移: f ( x − τ s ) = e − ( x − 10 ) 2 f(\frac{x - \tau}{s}) = e^{-(x-10)^2} f(sx−τ)=e−(x−10)2 就变成了下面这样子 如果缩放一下尺寸呢: f ( x − τ s ) = e − ( x − 10 5 ) 2 f(\frac{x - \tau}{s}) = e^{-(\frac{x-10}{5})^2} f(sx−τ)=e−(5x−10)2
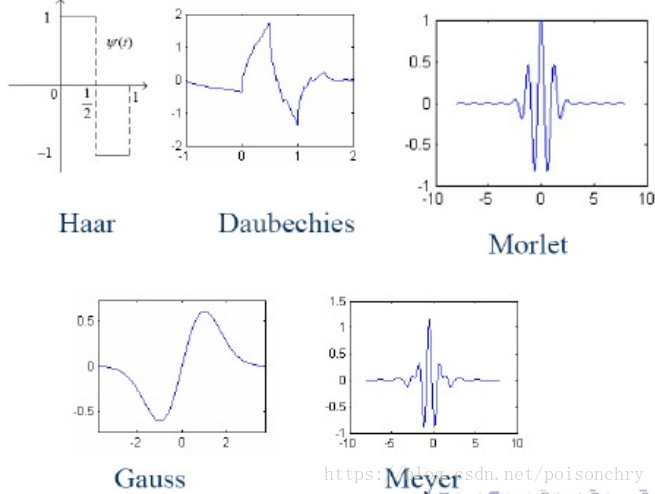
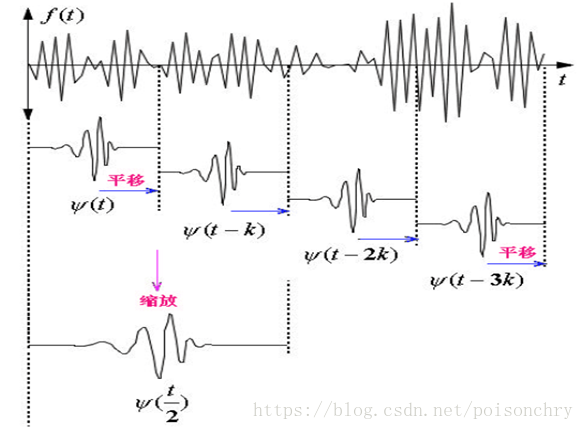
这些其实是非常简单的高中数学知识。同理,对于我们的小波核,或者说小波基函数来说: ψ ( x − τ s ) \psi (\frac{x - \tau}{s}) ψ(sx−τ) 正是通过这样简单的方式完成对小波频率、相位的变化控制的。在公式的表达方面,小波函数与短时傅里叶、以及卷积有非常相似的过程,都有滑动窗口处理原函数的概念,但是仍然有一些不同之处: 短时傅里叶分析:在同一个时间窗口内,会用到不同频率的正弦函数对原函数进行取样小波分析:在同一个时间窗口内,只会用一个小波核对原函数做哈达玛积卷积:在滑动时间窗口内,对核函数翻转后,再求哈达玛积从我们之前做傅里叶、以及卷积的过程我们可以得出一个经验性的推断,那就是不同特征、频率的小波在做了哈达玛积后,我们应该可以得到与小波,以及原信号特征的高度相关的信号组成内容,这个时候我会联想到PCA。不过这些内容我打算在其他章节,聊数据挖掘和AI的时候再详细解释。 我们先来说说数学家设计小波的一个主要构想,就是利用这种特征敏感性,提取一个包含了时域、和频域信息的工具,有针对性的处理原始信号中我们感兴趣的成分。 但是在我们进入小波分析之前,先说点其他的。 时域信号的基本特点相较于傅里叶分析,小波有分析处理连续信号、间断信号的强大能力,所以很多时候信号学会放弃使用耗时的傅里叶而使用小波来处理这些问题。但是这也带来了其他新问题,比如观察尺度的问题。 观察尺度的问题所谓观察尺度问题,是对应于连续信号才会存在的问题。对于全时域例如傅里叶来说,尽管可以分析所有频率,但无法有效处理间断信号,或者持续不断变化的连续信号。 如果采用固定窗口或者大小的短时傅里叶,窗口尺度过大,会导致处理效率降低;此外,那么对于高频信号又会在处理后的频谱上表现过于“普通”,而导致我们在观察的时候忽略掉。 如果观察尺度过小,又会导致无法有效分析一些低频信号。因为高频信号有快速振荡的特点,可以在较短的观察周期里清晰的看见,而低频信号由于振荡较慢,所以需要一个较长的观察周期才能够发现。 低频信号 ——> 振荡较慢 ——> 需要较长的观测周期 ——> 频域上能有更好的体现高频信号 ——> 振荡较快 ——> 需要较短的观测周期 ——> 时域上能有更好的体现所以观察尺度的大小选择,这是非常关键的一步。其次,由于小波函数具有不同的波形特征,所以就像卷积函数一样,如果想要获得理想的效果,需要仔细的选择合适的小波函数。 小波函数为了彻底理解小波变换的原理,你首先需要把小波函数 ψ ∗ \psi^* ψ∗ 当成一个时域滤波器,只不过这个滤波器和我们常见的滤波器,例如二阶的高斯滤波器,一阶的带通滤波器,或者其他样条滤波器不太一样,小波函数之所以叫小波(Wavelet),顾名思义: 它有在有限位置振荡,积分为0。此外,小波函数具有可以拉伸和压缩等较其他常用的滤波器所不一样的特点。 这些是比较常用的小波函数,它们都是在有限空间里振荡能量衰减,并且积分为0的函数。由于小波本身具备滤波器的性质,所以要知道过滤后的信号的形态特征上,多多少少会带上小波函数的形态特征。 所以你也许要多实验不同的小波核,通过计算后得到的效果,来决定实际生产环境中到底使用什么核函数更合适一点,甚至你也可以考虑把多个小波函数结合起来一起使用,以获取更好的效果。 那么接下来,我们来研究一下小波是怎么工作的。 对原始信号的小波分解由于小波函数的振荡特点,所以当我们对X轴进行压缩,可以得到高频信号,反之可以得到一个低频信号。但是与直觉相反的是 ψ ( s , τ ) = f ( x − τ s ) \psi(s, \tau) = f(\frac{x-\tau}{s}) ψ(s,τ)=f(sx−τ),获得高频信号是通过令 0 < s < 1 0< s < 1 0 1 s>1得到。 由于小波函数只在有限区间内振荡,所以需要在每次计算完毕后,对小波函数进行平移,从 T 0 T_0 T0,移动到 T 1 T_1 T1 然后对原信号做一次元素积,再移动到下一个时刻 T 2 T_2 T2,一直覆盖完毕全部原始信号。 所以它和卷积最大的不同,是小波的计算过程是周期性的平移,而不是平滑移动。当然,这只是理论上,而在实际的操作中,会把小波按照卷积的方式进行滑动。所以,比如对于心跳信号ECG的估计中,会看到小波函数有类似的运用。
回到示例图表示计算过程,我们可以看到小波变换总是从最小尺度(也就是最高频率)开始计算,需要注意一点就是尺度和频率的换算方式 f r e q = 1 / s c a l e freq = 1 / scale freq=1/scale 第一次计算 第二次计算 第三次计算
如果我们把每次计算后的值都plot到图上,并且以三维形式展现出来,大概就是这样的:
可以看到随着频率的降低(频率与尺度成反比关系),有效信号量越少。从Scale轴看,0-50包含了原始信号中最多的有效信号,而信号主要集中在Translation轴,60-100的范围内。而从原始信号来看,也基本上符合我们的推断。
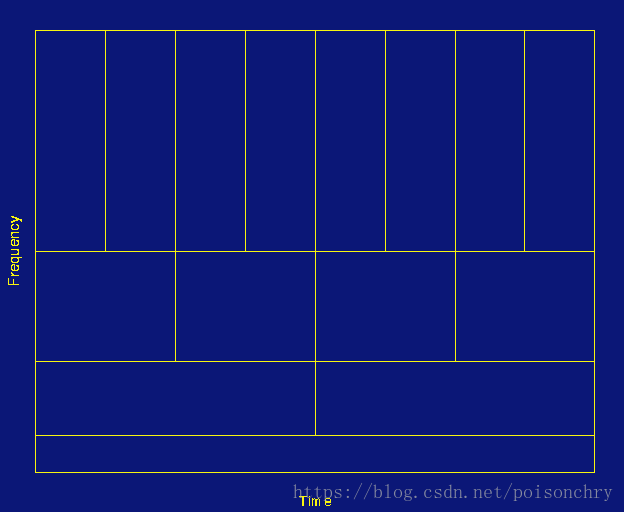
在某些文章或教程里,你可以看到这样一个格子用来说明小波的特点,但在中文教材里缺很少会详细解释这个格子的意思 格子的横坐标代表时间坐标t,纵坐标代表的是频率,格子的数量从最下层到最上层,数量以 2 n 2^n 2n增加,这告诉我们,随着频率增高,需要的计算次数也在增加; 每个格子的面积,也就是小波函数振荡部分对原信号函数的积分区域是一样的,这使得小波在不同尺度上,可以尽最大可能覆盖对应的频率范围,换句话说,就是用大尺度小波函数对信号中低频信号进行积分,可以最大尺度捕捉到低频信号部分,反之则是高频信号。 所以,由于各格子的宽度,也就是观测窗口,是随着频率一起调整,所以这也是小波分析相较于短时傅里叶,说它是一种动态分析的原因。 那么在下一章里,我们就来着手实现一个简易的小波分析吧~~ |
【本文地址】
今日新闻 |
推荐新闻 |




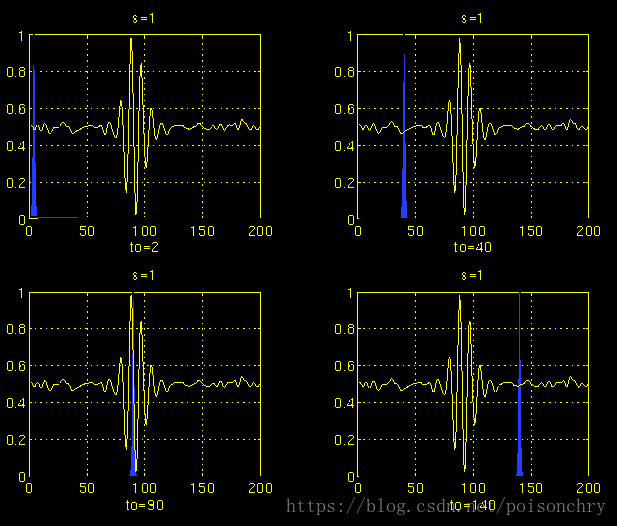
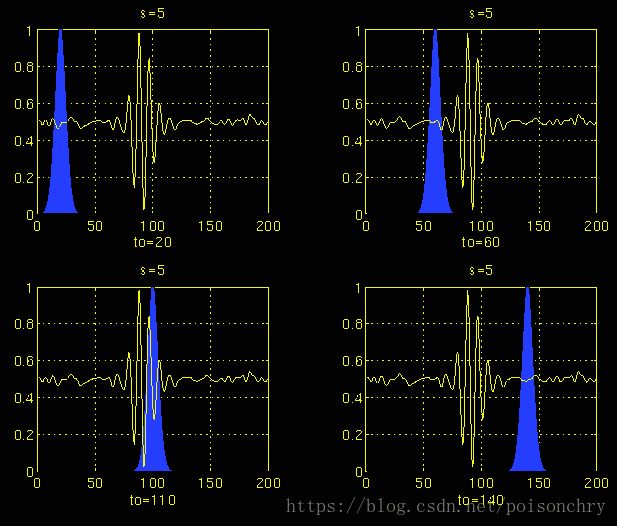
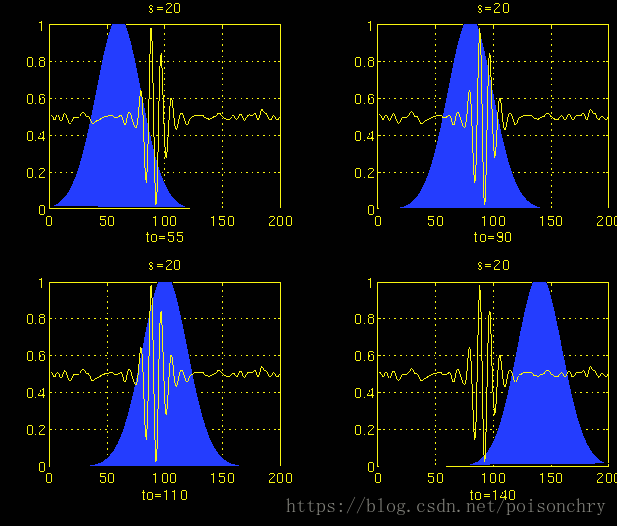 其中蓝色部分,就是小波函数,黄色的信号代表原始信号。
其中蓝色部分,就是小波函数,黄色的信号代表原始信号。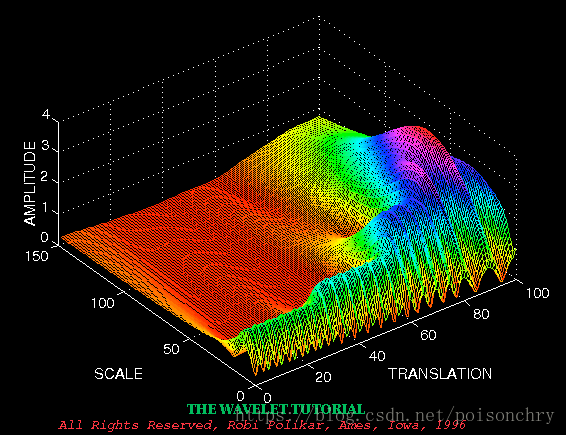 这图里的坐标系和我们通常的有所不同,坐标系的原点是再图的右下方,你需要注意的就是Scale轴,它表示每次计算时所用小波的频率。
这图里的坐标系和我们通常的有所不同,坐标系的原点是再图的右下方,你需要注意的就是Scale轴,它表示每次计算时所用小波的频率。