对称矩阵到三对角矩阵的Lanczos推导(python,数值积分) |
您所在的位置:网站首页 › 对角矩阵python › 对称矩阵到三对角矩阵的Lanczos推导(python,数值积分) |
对称矩阵到三对角矩阵的Lanczos推导(python,数值积分)
|
第三十二篇 Lanczos转化到三对角形式
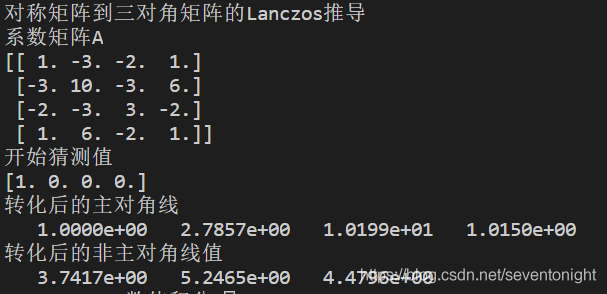
在之前的篇章里,有许多求解线性方程的迭代方法,如最陡下降法,可以通过向量乘法和各种简单的向量运算,简化为一个单个矩阵的循环。将矩阵化为三对角形式的Lanczos方法,保留其特征值的同时,使用类似的计算方式,实际上与共轭梯度法相关联。 在这种方法中,变换矩阵[P]是用相互正交的向量构造的。通常我们求对称矩阵的特征值由下式开始: 将上式的第一,第二和第三分别乘以{p}T, {q}T和{r}T,并注意向量的正交性,得到 构造“Lanczos向量”{p}、{q}和{r},并求解三对角形式αi和βi,可以遵循以下算法: 1)开始猜一个单位长度的向量{p}(如[1 0 0]T) 2)通过方程2,计算α1 = {p}T [A]{p} 3)通过方程1,计算β1{q} = [A]{p}−α1{p} 4) {q}的长度是一个单位,因此通过正交化计算β1和{q} 5)由方程2,计算α2 = {q}T [A]{q} 6)有方程1计算β2 {r} =[A]{q}−α2{q}−β1{p} 7) {r}是单位长度,因此通过正交化计算β2和{r} 8)由式2计算α3 = {r}T [A]{r}等。 通常,对于一个n × n矩阵[A],将[P]的正交向量列记为{y}j, j = 1,2,···,n,程序使用的算法如下(设β0 = 0) 终端输出结果 |
【本文地址】
今日新闻 |
推荐新闻 |
 确保[P]T [P]=[I]的一种方法是构造互相正交的,单位长度的正交化向量,如{P}, {q}和{r}构造[P]。以3 × 3矩阵为例,可以得到
确保[P]T [P]=[I]的一种方法是构造互相正交的,单位长度的正交化向量,如{P}, {q}和{r}构造[P]。以3 × 3矩阵为例,可以得到  在Lanczos方法中,要求得到的[P]T [A][P]是一个对称的三对角矩阵
在Lanczos方法中,要求得到的[P]T [A][P]是一个对称的三对角矩阵 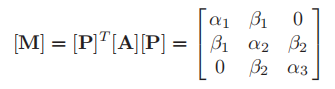 所以
所以  因为[P]是由正交向量组成的
因为[P]是由正交向量组成的 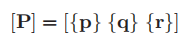 可以展开上面的式子
可以展开上面的式子 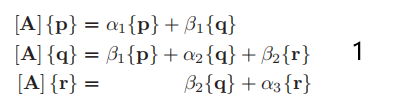
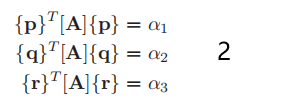
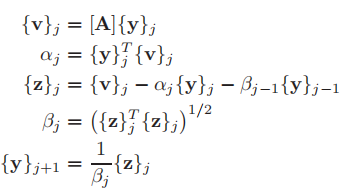 程序如下:
程序如下: