在物理学习过程中，我们往往会遇到一个量——密度，它是我们计算连续分布的质量、电荷量、电流等的有利工具。

    初中物理对密度的定义是：单位体积物质所具有的质量。这是一个比较狭义的概念，其准确名称应当是“质量体密度”。但是，在学过了高中乃至大学的物理后，你会发现密度并不仅仅是如此。那么，广义的密度和初中涉及的ρ=m/V究竟有怎样的不同呢？

1、不同维度物体的密度

    我们要想定义一个物体的体密度ρ，那么至少它得有体积。但是在物理学的模型中，有一些物体是没有体积的，比如二维的曲面（平面）与一维的曲线（直线）。这个时候定义单位体积的质量没有意义，因此只得把“单位体积”改成“单位面积”或者“单位长度”，于是也就诞生了面密度σ与线密度λ，它们分别对应上述的单位面积与单位长度。

    （注：以下的λ、σ、ρ与前文的定义一致，分别是线密度、面密度、体密度，可能与一些教材上不同，请注意区分。）

2、由密度计算质量

    对于均匀的物体，不论其维度如何，总是可以有相应的密度来计算其质量。例如，均匀曲线长为L，则其质量为λL；均匀曲面面积为S，则其质量为σS；均匀三维几何体体积为V，则其质量为ρV。

    当然，在实际情况下总是会遇到不均匀的物体，此时直接用密度乘以长度/面积/体积（统称测度），是无法算出其精确质量的。当然，我们不能排除我们知道它的平均密度，此时用密度平均值乘以测度则还是可以的；如果没有这等好事，我们便只能利用微积分。在微积分的意义下，密度是一个与位置有关的函数，因为一个物体不均匀指的就是它不同位置的密度有不同。

    此时，我们还是要明确微积分的意义——求和，你把积分号∫看成求和号Σ或许会更形象。一条与x轴平行的直线段上取长度为△x的一小段，那么对应的质量就是λ△x，其中λ是x的函数；整条线段的质量就是Σλ△x=∫λdx。这里的∫是定积分，积分限则是线段上的点x坐标的上下限。当这条直的线段弯成一条曲线时，光分析其x坐标已经没有意义，只能暂且抛弃坐标系，选择直观的弧长微元ds，那么一小条曲线弧上的质量就是λds，求和就有总质量∫λds。这是第一类曲线积分，我们在此先不管它怎么计算，但是大家应该理解曲线积分的意义，否则将不知道自己高数题中究竟在计算什么。

    对于二维物体，如果是平面区域，则用面积微元计算质量，m=∫∫σdxdy，这是二重积分，其中σ是关于x和y的二元函数；如果弯成曲面，则选择曲面上的小面积dS做积分，m=∫∫σdS，这是第一类曲面积分。对于三维物体，则用体积微元dxdydz（或写成dV）的三重积分，m=∫∫∫ρdV，其中ρ是x，y，z的三元函数。

    有了密度的概念之后，我们对数学上各种各样积分的实际意义将会有更深刻的认识；另外，对于电荷量的求解，和质量是一模一样的，之前的质量密度，改成电荷密度就好了。

3、高维物体密度的不同表示方式

    说了这么多，我们似乎下意识地规定了一件事：一维物体只能有线密度，二维物体只能有面密度，三维物体只能有体密度。第一句话是正确的，一维物体确实无法定义面密度与体密度，因为它的维度的确不够高。但是后两句话的正确性值得商榷。

    我们想象一个情景：有一块矩形的二维平板，如果按照二重积分的方式把它分成一个个面积微元，那么它将是这样的：

    我们仔细观察这个图，发现这种方式分得的每一小块，无论长还是宽都非常小。那么，如果换一种方式呢？

    在这种分割方式下，不是一块一块，而是一条一条，尽管所谓的一条其实也只是拉得比较长的一块。这些条状物在横向的长度不是小量，而是正好等于矩形的横边长；在纵向的宽度才是无限小的。

    两种分割方式用于计算这个矩形的质量，显然是有区别的。看上去都是分割求和，但是前一种由于把面积分得太细，必须用二重积分（计算的时候往往需要化成两次定积分），也即两步才能得到整个矩形，当然它对所有的密度分布都是适用的；但是，如果我们简化一下问题，比如这个矩形的面密度只与纵向坐标有关，那么何不采用后一种方法？截取一个小条，并且保证其长度恰好是矩形的横边长，那么这个小条的质量就只取决于小条的宽度。在这个时候，我们定义单位宽度的小条的质量为λ（不一定是常数），则对于纵向宽度为dy的小条，其质量就是λdy，从而矩形的质量就是一条条质量的加合，m=∫λdy，成了定积分，那么一步即可得到总质量。我们发现，在这种简化了的情形下，用一维的思路同样可以计算二维物体的质量。于是，我们似乎又定义了二维物体的线密度，它实际上是我们忽略掉一个维度之后的产物；之所以能忽略，是因为密度与这个维度的坐标无关。

    在三维物体中也可以有类似的定义：一个长方体，长a宽b高c，分别沿x，y，z方向。如果其内部的密度分布与高度z无关，我们的分割就可以是一个个与原长方体高度相同的小柱体（也就是不拦腰切割），此时，我们可以定义单位底面积的这种柱体的质量，它就相当于一个面密度；如果密度分布与x和z都无关，那么在这两个方向都不必切割，直接将长方体分成一片片长a高c的薄片，定义单位厚度薄片的质量，那么这就相当于一个线密度。后一种定义在一些电磁学的问题中也会用到，例如，对于一根均匀带电的圆柱形导线，尽管它是有粗细的，是三维物体，但是我们仍然可以定义一个单位长度的电荷量λ，这里的“长度”指的就是在圆柱母线方向上的长度。

    以上的定义相当于一个降维的过程，在简化计算方面具有非常重要的作用，而我们需要做的则是理解物理问题中铺天盖地的密度究竟都是什么意思。

4、密度转化与薄壳法

    这里所说的主要是数学上做微积分的一个技巧，对物理的一些问题也很有帮助。

    在一些高等数学的教材中有“薄壳法”这一名词，这是微元思想的一个集中体现。其实我们前面所说的高维物体的面密度、线密度，就是这种思想的一个实例——当一个函数值的分布在一个方向上具有某种不变性时，我们可以选择不在这个方向上进行切割，而是直接在真正会对函数值有影响的维度上进行分割求和，从而减少积分的次数。当然，即使这个维度对应的变量会影响函数值，只要能够把这种影响用其他变量表示，那么这个维度上的积分同样可以略去。

    举个例子：一个圆柱，底面半径为R，高为h，其轴线与z轴重合，上下底面的圆心分别在(0,0,h)与(0,0,0)，其质量体密度ρ=kz（k为常数），求其质量。

    我们当然可以用三重积分∫∫∫ρdxdydz=∫∫∫kzdxdydz，亦或是转化为柱坐标∫∫∫kzrdrdθdz。但是，当我们发现这个圆柱的质量体密度只和z有关时，我们就可以预知，这个质量应该只需要对z积分一次就够了。于是我们把圆柱在z方向切成一个个圆柱薄片，厚度为dz，则z处薄片的质量为dm=kz·πR²dz。将这个式子从0到h求和，即得到圆柱质量m=kπR²h²/2。这种做法本质上与柱坐标的三重积分一致，但是我们直接跳过了对r和θ积分的步骤。

    在这个情况下，我们利用一下前文讲的，因为密度只和高度z有关，于是我们定义单位高度薄片的质量λ=dm/dz=kz·πR²。这就是我们定义的这个圆柱体的“线密度”。当我们已经有了这样一层认识之后，用m=∫λdz就可以轻松算出圆柱的质量。

    与此同时，我们发现，均匀直柱体的“线密度”与体密度存在如下关系：λ=ρπR²。线密度等于体密度乘以底面积！与此同时，对于我们前面讲的那个矩形，设其面密度为σ，则宽度为dy的窄条质量dm=σ·ady。从而线密度λ=dm/dy=σa。线密度等于面密度乘以横向长度！这样一来，我们就把几个密度联系起来了。当然，有这种联系的前提是模型是简化的，也就是上文所说，密度分布与某一个坐标无关，或是与某个坐标的关系可以用其他坐标表示出来。

    我们用这个思想解决电磁学中的一个问题：已知电荷线密度λ、半径为R的均匀带电圆环，其轴线上距离圆心x处的电场强度为：

    如何用这个公式解出电荷面密度σ、半径为R的均匀带电圆盘轴线上x处的电场强度？

    圆环与圆盘的区别在于，一个空心，一个实心；或者说，一个一维，一个二维。圆盘的电场强度，如果用原始方法算，要使用二重积分，而且还是矢量加合，需要先投影再计算，比较麻烦；但是，使用薄壳法只需定积分。

    我们不妨思考：圆环与圆盘有什么联系？此时薄壳法就发挥了它的作用：将圆盘由内而外看成一个个圆环的嵌套，那么对每个圆环使用已知的公式，再把这些圆环的电场求和，即可得到整个圆盘的电场。

    我们用上图的方式计算：在圆盘上取一个半径为r、宽度为小量dr的圆环，于是这个圆环对轴线上x处的电场就是上述的公式，将R改成r即可。但是，这个圆环的电荷线密度λ怎么确定？自然是由圆盘的面密度σ得到。虽然这个圆环有宽度，但是我们仍然可以定义在切向单位长度的小条带有多少电荷——λ=dq/2πr=σ·2πrdr/2πr=σdr。事实也的确如此，因为我们做的是把2πr的一圈去切割，看一小段上的电荷，因此这里的“横向长度”就是dr，正好和之前的线密度=面密度×横向长度是一致的（熟练之后λ=σdr可以直接写出）。于是我们可以得到一个圆环在轴线上x处产生的电场强度

    对r从0到R积分，可以得到圆盘产生的总场强

    我本人还曾经使用过相当骚的操作：计算均匀实心正方形相对中心的转动惯量，我将正方形分成一个个方框的嵌套，先算空心方框的转动惯量（平行轴定理），然后再积分。当然，把正方形分成一个个横（竖）条，也是可行的。

5、关于电流密度

    前面的密度或许还是比较好理解的，但是很多人在学习到电流密度的时候，会产生很大的疑惑，因为电流体密度不是单位体积的电流而是单位面积，电流面密度不是单位面积而是单位长度。这个定义是否有矛盾的地方？

    这里我们需要明确一点：电流和我们前面所说的质量、电荷量是不一样的。如果说可以把一个电荷比作一个人，那么一条电流就相当于是一支队伍。电流密度数的是有几支队伍而不是有几个人。队伍和人的最大区别就在于，队伍是有长度的，这个长度本身就占据着一个维度。对于二维分布的电荷，我们把面积在x，y两个方向都取得无限小，也就是把二维区域分成一块块小的dxdy，那么把这些小块加起来即可得到整个区域内的总电荷量；但是电流则不然，我们不可以用刚才二重积分的方式计算二维分布的电流，因为有很多小块实际上属于同一根电流（如下图中的两个小正方形，它们都是面积微元，包围住的是同一根电流），这样求和会造成严重的重复计算。因此，二维分布的电流，谈单位面积有多少电流是不行的，我们只能退而求其次，像下图一样，在垂直电流前进的方向上划一条线（图中红线），看看上面单位长度上穿过了多少根电流线？这才是电流的面密度。至于三维分布的电流，我们同样只能用单位面积上穿过了多少根电流线来衡量电流的体密度。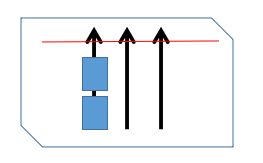

    好了，以上就是我们关于密度的一些讨论，或许篇幅比较长，但是我们保证了内容的完整性与实用性。现在很多的数学与物理教材往往只是轻描淡写地介绍电流密度的概念，对于质量、电荷量的线密度、面密度、体密度则更是不做任何研究，没有考虑到这种做法对读者的坏处。我希望这篇文章多少可以起到一个补足的作用，让大家能够真正理解密度，在具体情境中用到密度时也有方向可寻，同时对维度也有一个更为形象的认识。