用梯形法求定积分的值 |
您所在的位置:网站首页 › 定积分定义法求极限 › 用梯形法求定积分的值 |
用梯形法求定积分的值
|
一、梯形法求解定积分的过程
1.求定积分值存在的问题
计算定积分是数值计算领域内的一个重要内容。对于能够得到原函数的被积函数,如:
其定积分可以直接计算。 但对于不易得到原函数的被积函数,可以考虑使用数值计算的方法得到近似值。如: 不易得到原函数,故其如下 的定积分也不容易求解。 2.定分积的几何意义定积分的几何意义是被积函数和x轴以及积分上限、积分下限之间围成的图形的面积。如下图所示: 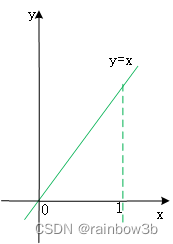 图1 定积分几何意义
图1 定积分几何意义
图中x轴、y=x与y=1所围三角形的面积即为 对于无法得到原函数的被积函数,其定积分也是这样的面积。如下图所示: 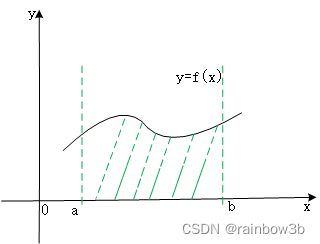 图2 定积分几何意义
图2 定积分几何意义
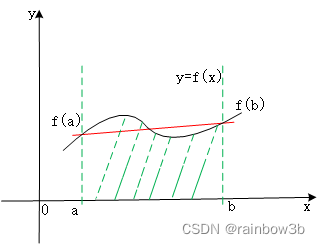
上图中,x轴、f(x)、a、b等所围成的阴影面积即为 的值,即以a为积分下限、b为积分上限、被积函数f(x)的积分值。 3.积分数值计算过程图2中的阴影面积是不容易得到的。可以用近似的方法得到,即梯形近似法。如下图所示:
在f(a)、f(b)之间直接连线,则可以由x轴、a、b、以及连线形成梯形。该梯形的两个底分别为:f(a)、f(b),高为(b-a),由梯形的面积公式,可以得到上图中所围梯形的面积为:
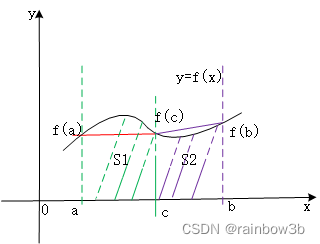
这个可以作为 如果对上图进一步分割,按下图进行拆分,
设c为积分下限a、积分上限b的之间中点,则 以f(c)为线对图形进行分割,形成两个梯形,分别计算面积,再对面积求和。 梯形S1的两个底分别为f(a)、f(c),高为(c-a);梯形S2的两个底分别为f(c)、f(b),高为(b-c)。则面积: 同样, 这样,总的面积是: 令(式1)为
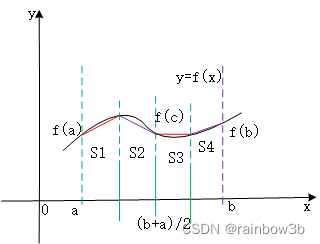
如果对上图中S1、S2再进行等分分割,可以得到如下图的S1、S2、S3、S4四个梯形。再次分别计算其面积后进行求和,可以得到更近似的面积,即定积分值。如此,不断进行将[a,b]进行二分,递推下去,得到的积分值越来越精确,可以无限逼近函数f(x)在[a,b]上的定积分。
这样可以得到递推公式。具体是:将[a,b]段分为n等分,一共有n+1个等分点,第k(k=0,1,2...n)个等分点的值为: 用
利用上式,即可以得到定积分的近似值。设置某一个精度e,当 由于x不能为0,且 |
【本文地址】
今日新闻 |
推荐新闻 |