旋转向量与欧拉角 罗德里格斯公式(Rodrigues's Formula) |
您所在的位置:网站首页 › 威廉罗德里格斯 › 旋转向量与欧拉角 罗德里格斯公式(Rodrigues's Formula) |
旋转向量与欧拉角 罗德里格斯公式(Rodrigues's Formula)
|
旋转向量
旋转矩阵表达方式
旋转矩阵描述旋转,变换矩阵描述一个6自由度的三维刚体运动。但存在如下缺点: SO(3)的旋转矩阵有9个量,但一次旋转只有3个自由度。因此这种表达方式是冗余的。同理,变换矩阵16个量表达了6个自由度的变换,也不够紧凑。旋转矩阵自身带有约束:它必须是个正交矩阵,且行列式为1。变换矩阵也是如此。当想要估计或优化一个旋转矩阵/变换矩阵时,这些约束会使得求解变得困难。 外积与旋转的关系外积表达了两个向量的旋转关系。对于坐标系的旋转,任意旋转可以用一个旋转轴和一个旋转角来刻画。可以使用一个向量,器方向与旋转轴一致,而长度等于旋转角。这种向量称为旋转向量(或轴角,Axis-Angle)。这种表示法只需要一个三维向量即可描述旋转。同样,对于变换矩阵,我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的位数正好是六维度。 旋转矩阵和旋转向量之间的转换旋转轴n,角度为 θ \theta θ,对应的旋转向量 θ \theta θn。从旋转矩阵到旋转向量的转换过程由罗德里格斯公式(Rodrigues’s Formula)表明。 罗德里格斯公式推导
在计算机图形学中,罗德里格向量旋转公式通常被用来填写旋转矩阵。如果把k 和v分别写为列向量: ( k x k y k z ) \left( \begin{matrix} k_x \\k_y \\ k_z \end{matrix} \right) ⎝⎛kxkykz⎠⎞, ( v x v y v z ) \left( \begin{matrix} v_x \\v_y \\ v_z \end{matrix} \right) ⎝⎛vxvyvz⎠⎞ 则旋转以后的向量可以表示为 v r o t _{ rot} rot=Rv 其中 R=cos θ \theta θI+(1-cos θ \theta θ) ( k x k y k z ) \left( \begin{matrix} k_x \\k_y \\ k_z \end{matrix} \right) ⎝⎛kxkykz⎠⎞ ( k x , k y , k z ) (k_x,k_y,k_z) (kx,ky,kz)+sin θ \theta θ ( 0 − k z k y k z 0 − k x − k y k x 0 ) \left( \begin{matrix} 0&-k_z&k_y \\k_z&0&-k_x \\ -k_y&k_x&0 \end{matrix} \right) ⎝⎛0kz−ky−kz0kxky−kx0⎠⎞ 其中,I是3阶单位矩阵。需要注意的是,公式中的第二项不是点积,而是张量积,得到的是一个3行3列的矩阵。 转换结果R = c o s θ =cos\theta =cosθI+(1-cos θ ) \theta) θ)nn T ^T T+sin θ \theta θn^ 符号^是向量到反对称的转换付。。可以从一个旋转矩阵到旋转向量的转换。对于转角 θ \theta θ,有: tr(R)=cos θ \theta θtr(I)+(1-cos θ ) \theta) θ)tr(nn T ^T T)+sin θ \theta θtr(n^)=3+cos θ \theta θ+(1-cos θ \theta θ)=1+2cos θ \theta θ 因此: θ \theta θ=arccos( t r ( R ) − 1 2 \frac{tr(R)-1}{2} 2tr(R)−1) 关于旋转轴n,由于旋转轴上的向量在旋转后不发生改变,说明 Rn=n 因此,转轴n是矩阵R特征值的1对应的特征向量。求解此方程,在归一化,就得到了旋转轴。“旋转轴经过旋转之后不变”。 欧拉角欧拉角,使用3个分离的转角,把一个旋转分解成3次绕不同轴的旋转。分的细一些还可以分每次是绕固定轴旋转还是绕旋转之后的轴旋转。 航空和航模中,“偏航-俯仰-滚转”(yaw-pitch-raw)3个角度来描述一个旋转。等价于ZYX轴的旋转。 欧拉角的一个重大缺点是会碰到万向锁问题(Gimbal Lock):在俯仰角为 ± 90 ° \pm 90° ±90°时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失一个自由度(由三次旋转变成了两次旋转),这杯称为奇异性问题。只要想用3个实数来表达3维旋转时,都会不可避免地碰到奇异性问题。由于这种原理,欧拉角不适合于插值和迭代,往往只用于人机交互中。SLAM中也很少直接用欧拉角表达姿态,同样也不会在滤波或优化中是哟个欧拉角表达旋转(因为它的奇异性)。验证算法是否有错,转换成欧拉角能快速分辨结果是否正确。 |
【本文地址】
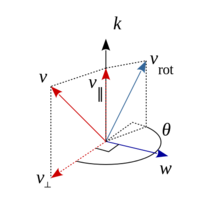 v
∣
∣
_{||}
∣∣与旋转向量v与旋转轴k(k为当我向量)相互垂直。对于与旋转轴呈任意角度的向量v,可以通过正交分解,把被旋转向量转化为与旋转轴平行的分量v
∣
∣
_{||}
∣∣和与旋转轴垂直的分量 v
⊥
_{\bot}
⊥,其中与旋转轴平行的分量v
∣
∣
_{||}
∣∣在旋转中是不变的,而与旋转轴垂直的分量 v
⊥
_{\bot}
⊥则恰好旋转了角度
θ
\theta
θ,把与旋转轴平行的分量与旋转以后的与旋转轴垂直的分量加在一起,即可得到旋转以后的分量。 对向量 v做正交分解: v= v
∣
∣
_{||}
∣∣+ v
⊥
_{\bot}
⊥ 利用向量投影公式,可以得到 v
∣
∣
_{||}
∣∣的表达式: v
∣
∣
_{||}
∣∣= (v
⋅
\cdot
⋅k)k 通过减法,得到 v
⊥
_{\bot}
⊥=v-v
∣
∣
_{||}
∣∣=v-(v
⋅
\cdot
⋅k)k 利用外积可以计算与v
⊥
_{\bot}
⊥和k都垂直,且长度为v
⊥
_{\bot}
⊥的向量w: w=k
×
\times
×v
⊥
_{\bot}
⊥=k
×
\times
×(v-(v
⋅
\cdot
⋅k)k)=k
×
\times
×v 旋转以后的向量可以表示为: v
⊥
r
o
t
=
_{\bot rot}=
⊥rot= cos
θ
\theta
θ v
⊥
_{\bot}
⊥+sin
θ
\theta
θw=cos
θ
\theta
θ(v-(v
⋅
\cdot
⋅k)k)+sin
θ
\theta
θk
×
\times
×v 与v
∣
∣
_{||}
∣∣相加即可得到旋转以后的向量的表达式: v
r
o
t
_{ rot}
rot=v
∣
∣
_{||}
∣∣+ v
⊥
r
o
t
_{\bot rot}
⊥rot=cos
θ
\theta
θv+(1-cos
θ
\theta
θ)(v
⋅
\cdot
⋅k)k+sin
θ
\theta
θk
×
\times
×v
v
∣
∣
_{||}
∣∣与旋转向量v与旋转轴k(k为当我向量)相互垂直。对于与旋转轴呈任意角度的向量v,可以通过正交分解,把被旋转向量转化为与旋转轴平行的分量v
∣
∣
_{||}
∣∣和与旋转轴垂直的分量 v
⊥
_{\bot}
⊥,其中与旋转轴平行的分量v
∣
∣
_{||}
∣∣在旋转中是不变的,而与旋转轴垂直的分量 v
⊥
_{\bot}
⊥则恰好旋转了角度
θ
\theta
θ,把与旋转轴平行的分量与旋转以后的与旋转轴垂直的分量加在一起,即可得到旋转以后的分量。 对向量 v做正交分解: v= v
∣
∣
_{||}
∣∣+ v
⊥
_{\bot}
⊥ 利用向量投影公式,可以得到 v
∣
∣
_{||}
∣∣的表达式: v
∣
∣
_{||}
∣∣= (v
⋅
\cdot
⋅k)k 通过减法,得到 v
⊥
_{\bot}
⊥=v-v
∣
∣
_{||}
∣∣=v-(v
⋅
\cdot
⋅k)k 利用外积可以计算与v
⊥
_{\bot}
⊥和k都垂直,且长度为v
⊥
_{\bot}
⊥的向量w: w=k
×
\times
×v
⊥
_{\bot}
⊥=k
×
\times
×(v-(v
⋅
\cdot
⋅k)k)=k
×
\times
×v 旋转以后的向量可以表示为: v
⊥
r
o
t
=
_{\bot rot}=
⊥rot= cos
θ
\theta
θ v
⊥
_{\bot}
⊥+sin
θ
\theta
θw=cos
θ
\theta
θ(v-(v
⋅
\cdot
⋅k)k)+sin
θ
\theta
θk
×
\times
×v 与v
∣
∣
_{||}
∣∣相加即可得到旋转以后的向量的表达式: v
r
o
t
_{ rot}
rot=v
∣
∣
_{||}
∣∣+ v
⊥
r
o
t
_{\bot rot}
⊥rot=cos
θ
\theta
θv+(1-cos
θ
\theta
θ)(v
⋅
\cdot
⋅k)k+sin
θ
\theta
θk
×
\times
×v