数据研发学习笔记03:8种经典的统计学谬论 |
您所在的位置:网站首页 › 如何避免统计错误数据 › 数据研发学习笔记03:8种经典的统计学谬论 |
数据研发学习笔记03:8种经典的统计学谬论
|
文章目录
1 辛普森悖论 Simpson's Pradox如何避免
2 基本比率谬误 Base Rate Fallacy如何避免
3 伯克森悖论 Berkson's Paradox如何避免
4 罗杰斯现象 Will Rogers Phenomenon如何避免
5 幸存者偏差如何避免
6 赌徒谬论 Gambler's Fallacy如何避免
7 生日悖论 Birthday Paradox如何避免
8 蒙提霍尔悖论
本文主要围绕以下问题展开相应的数据研发相关知识的梳理与总结: 在统计学上有哪些谬论?为什么会有这些谬论?如何避免在数据分析过程中陷入这样的谬论。举例说明。 1 辛普森悖论 Simpson’s Pradox辛普森悖论指的是,数据集分组呈现的趋势与数据集聚合呈现的趋势相反的现象。 先看一个例子——Sophia和Carlo两家餐厅推荐指数,可以通过看男性和女性各组的评分,也可以看整体的评分。如下图所示: 这里的问题在于,只查看单独各组数据的百分比会忽略掉样本的大小,也就是评论者的人数。每个百分比都由推荐用户数与相对应的评论人数计算得到。Carlo’s 有更多的男性评论者,而Sophia’s 有更多的女性评论者,因此导致了矛盾的结果。 辛普森悖论的另一个有趣的现象表现在,分层组数据表现的相关性方向与整体数据表现的相关性方向截然相反。我们来看一个简化后的例子。假设我们有每周运动小时数与两组患者(分别为50岁以下和50岁以上的患者)患病风险的对比数据。以下是各组运动数据与患病可能性的散点图(左侧:小于50岁,右侧:大于50岁)。 相关性完全逆转了!如果只给出这张图结果,我们会得到这样的结论:运动增加了患病风险,这与我们从分层数据散点图中得到的结论完全相反。 运动如何既减少又增加疾病风险呢?其实并不然,要想弄清如何解决这个悖论,我们需要从数据的生成过程来考虑展示的数据和原因——是什么产生了这些结果。 如何避免辛普森悖论告诉我们在分析数据时,不能简单的将分组数据汇总相加,而要仔细观察分组数据的特征。为避免辛普森悖论出现,就需要斟酌个别分组的权重,以一定的系数去消除以分组资料基数差异所造成的影响,同时必须了解该情境是否存在其他潜在因素而综合考虑。 辛普森悖论的重要性在于它揭示了我们看到的数据并非全貌。我们不能满足于展示的数字或图表,我们需要考虑整个数据生成过程,考虑因果模型。一旦我们理解了数据产生的机制,我们就能从图表之外的角度来考虑问题,找到其它影响因素。 除了使用数据,我们需要运用经验和业务知识,或者向专家学习,来更好地进行决策。 2 基本比率谬误 Base Rate Fallacy基本比率谬误(base rate fallacy),是指对统计学上的忽略基本比率而导致的推论谬误。 基本比率对概率有重要影响。这很好理解:买矿泉水的人多呢,还是买香奈儿香水的人多?人群和需求概率明摆着,简直不是问题。但是人们往往会通过代表性来评估概率,忽视基本比率。代表性的意思是,通过比较 B 与 A 的相似程度来评估概率。例如,如果 A 能高度代表 B,人们就会认为 A 源自 B 的概率高。但如果 A 与 B 并不相似,人们就会认为 A 源自 B 的概率低。 经典问题:Jack 已经退休。那么他是图书馆员还是推销员? 需要考虑实际中推销员的比例远远大于图书馆员,而不能简单凭“退休”二字推测大概率为图书馆员。 根据美国的统计数据,一个40岁左右的女性患乳腺癌的概率大约为1%。如果她通过乳房影像学检查来测试自己是否患乳腺癌,被误诊患上乳腺癌的概率约为9%。那么问题来了:如果一位40岁的女性去做了乳房影像学检查,结果显示她患上乳腺癌。她真正患上乳腺癌的概率是多少?是91%吗? 回答91%的朋友,恭喜你犯了基本比率谬误(base rate fallacy),即忽略了基本比率导致的推论谬误。我们假设对1000人进行检查,根据下图计算结果可知,正确答案约为9%。由于患上乳腺癌的女性的基本比率本来就很小,加上乳房影像检查自身带有的误诊率,其实只有9%左右的人真的患上了乳腺癌。 假设同性恋染上 G 病的概率是异性恋的 9 倍,张三染上了 G 病,而我们对他的性取向一无所知。试问张三是同性恋的概率是多少? 如果回答 90%,恭喜你又犯了基本比率谬误。 事实上,如果我们不清楚同性恋和异性恋占整个群体的比率(即基本比率),就无法回答这个问题。 为方便起见,我们假定群体有 100 人,同性恋有 10 人(占 1/10 ),异性恋有 90 人(占 9/10 )。再假设异性恋染上 G 病的概率是 X,则同性恋染上 G 病的概率为 9X。我们可用下表表示各子群体的分布: 切勿忽略基本概率!在我们做出任何判断前,首先需要对基本比率有个大致的认识,否则很容易不小心就陷入统计的陷阱。 3 伯克森悖论 Berkson’s Paradox伯克森悖论,指的是两个本来无关的变量之间体现出貌似强烈的相关关系。 为什么很多人会觉得帅哥都是混蛋?做个简化的假设,当你找男生约会的时候最看重两个条件:长得是不是帅,对你是不是好。两者至少满足其一你才会考虑跟他约会,长得不帅的渣男压根没有机会。因此对你所有的约会对象而言,两者有了负相关,于是你可能产生出渣男长得帅、暖男长得丑的印象。 同样的,演员的演技和长相成反比、学生文化课成绩和体育课成绩成反比也是伯克森悖论的例子。 假设某学校在招收学生时,要求学生要么学习成绩好,要么体育成绩好。 所有的报考学生需要参加两门考试:文化(语数外),和体育(跑跳投)。最后,学校仅录取在任一考试中考到90分以上的报考学生。 所以能够被学校录取的学生,要么在文化考试中考到90分以上,或者在体育考试中考到90分以上,或者在两门考试中都考到90分以上。 现在如果我们分析这些被入取学生的成绩分布,会发现一个学生的学习成绩,和体育成绩是负相关的。因为那些体育成绩最好的学生(比如体育100分),他们的文化平均分为50分(假设他们的文化考试呈现正态分布)。而体育成绩最差的学生(比如体育成绩10分),其文化平均成绩为95分(因为只有超过90分的学生才被录取)。 因此,分析人员可能会得出结论:体育越好,文化成绩越差。文化成绩越好,体育越差。但这个结论显然是错误的。 如何避免考虑变量本身之间是否存在关系或忽略了部分样本(如帅哥都是混蛋,忽略了不是帅哥这部分群体,导致帅哥与混蛋看似具有强烈相关性)。 4 罗杰斯现象 Will Rogers Phenomenon罗杰斯现象,又称Will Rogers悖论,是指将某些事物从一个组移到另一个组,两组的平均值增大,虽然其中没有值变大。 之所以会出现这种情况,是因为当数据点从一个组重新归类到另一组的时候,如果这个点在原来组的平均线以下,但是在新组的平均线之上,那么这两个组的平均线都会提升。 这一悖论源于美国喜剧演员Will Rogers。他曾经开玩笑说,“当俄克流民离开俄克拉荷马州并且搬到加尼福尼亚州,他们同时提升了两个州的平均智力水平。” 举例说明,假设有6个人,分别为40、50、60、70、80、和90岁。现在将他们分为两组。第一组包括40岁和50岁的两人,因此组平均年龄为45岁。剩下的归入第二组,因此组平均年龄为75岁。 罗杰斯现象,导致我们在医学领域产生一些容易让人混淆的,似是而非的结论。 举例来说,前列腺特异抗原测试(PSA测试)可以帮助我们诊断前列腺癌。在没有发明这项测试前,很多人患了前列腺癌却不自知,因此他们被归入“健康”人群。而那些被确诊前列腺癌的患者,被归入“患者”人群。 有了PSA测试这项技术以后,很多人在年纪轻轻时也能通过该测试确诊自己是否患上前列腺癌。这部分人,就被移出“健康”人群,归入“患者”人群。 由于这个归类的变化,导致患上前列腺癌的“患者”人群,以及“健康”人群的平均寿命都得到了提高。因为“健康”人群中被移去一部分癌症患者,而这些癌症患者属于“轻度病患”(前列腺癌的致死率很低),因此“健康”和“患者”两个人群的寿命平均值均得到了提升,让人误以为PSA测试能够帮助我们延长寿命。 如何避免需考虑平均值变大的根本原因,斟酌两次计算平均值前后分组之间的变化。 5 幸存者偏差幸存者偏差也称“生存者偏差”或“存活者偏差”,是一种常见的逻辑谬误。指的是当取得资讯的渠道仅来自于幸存者时,因为只能看到经过某种筛选而产生的结果,而没有意识到筛选的过程,因此忽略了被筛选掉的关键信息,此资讯可能会存在与实际情况不同的偏差。 在“沉默的数据”、“死人不会说话”等等日常表达中,涉及幸存者偏差。此规律也适用于金融和商业领域,存活下来的企业往往被视为“传奇”,它们的做法被争相效仿,但其实有些也许只是因为偶然原因幸存下来了而已。 举例说明,在二战期间,人们发现幸存的轰炸机中,机翼中弹的数量很多,而机身中弹的却很少。因此人们认为我们应该加固飞机的机翼,其实不然,就是因为机翼中弹多还能飞回来,所以机翼中弹并没有影响飞机返航;而机身中弹的少则说明了子弹打中机身对飞机的影响更大,导致飞机不能返航,在这个飞机问题中,只统计到了幸存下来的飞机,以此下结论,是不正确的。 现实生活中也有很多幸存者偏差的案例,比如感觉周围都是本科以上的人,而实际上中国具备本科以上学历的人,只占总人口的3%。还有为什么感觉知乎上应届生人人都是月薪过万,因为你看到的都是月薪过万的人在答题,月薪低于1万的都处于沉默状态。 再比如媒体调查“喝葡萄酒的人长寿”。一般是调查了那些长寿的老人,发现其中很多饮用葡萄酒。但还有更多经常饮用葡萄酒但不长寿的人已经死了,媒体根本不可能调查到他们。 回到投资领域,在投资理财类电视节目中,我们经常看到取得成功的投资者谈论其投资经验和方法,但观众往往会忽略了一个事实:采用同样经验和方法而投资失败的人是没有机会上电视的。幸存者偏差现象可能导致以下的结果:(1)投资成功者出书出名,失败者将默默无闻,导致电视上大量专家在传经布道、市面上充斥着太多投资成功学类的书籍,可能会让观众或读者高估了通过投资获得成功的概率;(2)由于条件限制或者心理因素,投资成功者难以保证理性和客观,容易夸大自己能力、忽略运气因素、弱化当时所承担的风险等。 如何避免应对幸存者偏差的办法是双盲实验设计和详细全面客观的数据纪录,即“兼听则明”,抛掉对个案的迷信,全面系统的了解才能克服这个偏差。 对于如何消除幸存者偏差的误区,没有好的办法,但如果能做到以下几点,应该有些好处: (1)在投资领域,我们改变不了生存者偏差现象的存在,但我们可以努力不盲从所谓的权威; (2)对于基金、私募以及个人投资者的能力评价,要看长期的、最好是跨越多个经济周期的业绩记录; (3)为了使样本更反映事实,我们更应该搜集介绍投资失败的案例和总结,不但要向成功的人学习如何成功,更要从失败的人那里总结为什么失败,因为投资很大程度上是个避免失败的过程。 6 赌徒谬论 Gambler’s Fallacy赌徒谬误(Gambler’s Fallacy)亦称为蒙地卡罗谬误,是一种错误的信念,以为随机序列中一个事件发生的机会率与之前发生的事件有关,即其发生的机会率会随着之前没有发生该事件的次数而上升。如重复抛一个公平硬币,而连续多次抛出反面朝上,赌徒可能错误地认为,下一次抛出正面的机会会较大 赌徒谬误是生活中常见的一种不合逻辑的推理方式,认为一系列事件的结果都在某种程度上隐含了自相关的关系,即如果事件A的结果影响到事件B,那么就说B是“依赖”于A的。例如,一晚上手气不好的赌徒总认为再过几把之后就会风水轮流转,幸运降临。相反的例子,连续的好天气让人担心周末会下起大雨。 赌徒谬误亦指相信某一个特定的结果由于最近已发生了(“运气用尽了”)或最近没有发生(“交霉运”),再发生的机会会较低。 比如一个赌徒在打赌硬币是正面朝上或是背面朝上时的情景,前面5次的结果都是正面朝上,那么下一次他觉得反面朝上的概率会更大,这就是赌徒谬论。为什么说是谬论呢?因为高中的时候我们就学过扔硬币这个问题的概率,每扔一次一枚硬币是一个独立的事件,正面朝上和反面朝上的概率相同都是0.5,不受前面扔了多少次的影响,也就是说虽然前面5次都是正常朝上,下一次仍是正面朝上的概率也还是0.5。 聊到这,可能有些人会不理解了,或者脑海里依稀记得好像老师讲过,扔一枚硬币扔个1000次,正面朝上和反面朝上的次数都是接近一半的呀,能想到这里的同学,恭喜你,已经入门了。 确实如此,但请看清楚前提:扔1000次,这就是大数定理,当我们大量重复某一相同实验时,最后的结果会稳定在某一数值附近,但把大量重复事件的规律运用在少数的事情上就错了。 如何避免赌徒谬误的产生是因为人们错误的诠释了“大数法则”的平均律。投资者倾向于认为大数法则适用于大样本的同时,也适用于小样本。Tversky and Kahneman把赌徒谬误戏称为“小数法则”(law of small numbers)。 一个独立的事件并不会受前一个独立事件结果的影响。 大数定理不能用于单个独立事件。 7 生日悖论 Birthday Paradox生日悖论(Birthday paradox)是指,如果一个房间里有23个或23个以上的人,那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中,存在两人生日相同的可能性更高。对于60或者更多的人,这种概率要大于99%。从引起逻辑矛盾的角度来说生日悖论并不是一种悖论,从这个数学事实与一般直觉相抵触的意义上,它才称得上是一个悖论。大多数人会认为,23人中有2人生日相同的概率应该远远小于50%。 计算与此相关的概率被称为生日问题,在这个问题之后的数学理论已被用于设计著名的密码攻击方法:生日攻击。 假设你的班上一共有23位同学,其中任何两位同学生日撞期的概率为多少? 有人可能会这么想:一年有365天,把这23位同学分布在365天里,撞期的概率应该很小。大概不到10%吧。 事实上,23位同学中,生日撞期的概率为1/2。就是说,有一半的概率,这个班上至少有一对同学的生日相同。 对于这个问题,你可以这么考虑。我们先来算一下23位同学生日不撞期的概率。然后用1减去那个数字,就是这些同学生日撞期的概率。 假设23位同学排队逐个进入教室。第一个进入教室的同学,其生日和其他同学不一样的概率为1。第二位同学,其生日和其他同学不一样的概率为364/365。第三位同学,其生日和前面两位同学生日不一样的概率为363/365。 以此类推,所有同学生日不撞期的概率为1 X 364/365 X 363/365 … 然后用1减去上面的乘积,可以得出,当教室里有23个同学时,其结果为0.5左右。 以概率为依据做决策是不合逻辑的,然而逻辑和统计本身却是大不相同,在逻辑上,一个命题只有对和错两种划分,而在统计上,却可以说成对的概率有50%,错的概率为20%,就是这一点不确定性造就了以逻辑推理和统计为基础所得决策上的不一致,或者说矛盾,这就是统计关系不等于因果关系。 8 蒙提霍尔悖论蒙提霍尔悖论亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论、三门问题(Monty Hall problem)。三门问题(Monty Hall problem),是一个源自博弈论的数学游戏问题,大致出自美国的电视游戏节目Let’s Make a Deal。问题的名字来自该节目的主持人蒙提·霍尔(Monty Hall)。 假设你正在参加一个游戏节目,你被要求在三扇门中选择一扇:其中一扇后面有一辆车;其余两扇后面则是山羊。你选择了一道门,假设是一号门,然后知道门后面有什么的主持人,开启了另一扇后面有山羊的门,假设是三号门。他然后问你:“你想选择二号门吗?”转换你的选择对你来说是一种优势吗? 这个游戏的玩法是:参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门就可以赢得该汽车,而另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人会开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门会否增加参赛者赢得汽车的机会率?如果严格按照上述的条件的话,答案是会 「换门的话,赢得汽车的机会率是 2/3」。 这条问题亦被叫做蒙提霍尔悖论:虽然该问题的答案在逻辑上并不自相矛盾,但十分违反直觉。这问题曾引起一阵热烈的讨论。 |
【本文地址】
今日新闻 |
推荐新闻 |
 Carlo’s 在男性和女性推荐率上都赢了,但却输在了总体推荐率上!!!
Carlo’s 在男性和女性推荐率上都赢了,但却输在了总体推荐率上!!! 从图中我们可以清楚地看到数据负相关,表明增加每周运动量与两组患者患病率的风险降低相关。下面让我们将数据合并在一起再来看看他们的关系:
从图中我们可以清楚地看到数据负相关,表明增加每周运动量与两组患者患病率的风险降低相关。下面让我们将数据合并在一起再来看看他们的关系: 


 那么张三是同性恋的概率是:
那么张三是同性恋的概率是: 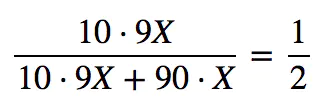 来自直觉的概率判断(9/10),只有在同性恋与异性恋比例相等时才适用。假定群体有100人,同性恋、异性恋各50人,则可用下表表示各种子群体的分布:
来自直觉的概率判断(9/10),只有在同性恋与异性恋比例相等时才适用。假定群体有100人,同性恋、异性恋各50人,则可用下表表示各种子群体的分布:  此时,张三是同性恋的概率是 90%:
此时,张三是同性恋的概率是 90%: 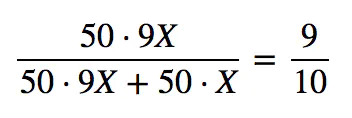
 现在把第二组中的那位60岁的哥们,移去第一组。移过去以后,第一组的平均年龄变为50岁,而第二组的平均年龄变为80岁。两组的平均年龄都上升了。
现在把第二组中的那位60岁的哥们,移去第一组。移过去以后,第一组的平均年龄变为50岁,而第二组的平均年龄变为80岁。两组的平均年龄都上升了。
