多重共线性的影响、判定及消除的方法 |
您所在的位置:网站首页 › 多重共线性相关系数检验 › 多重共线性的影响、判定及消除的方法 |
多重共线性的影响、判定及消除的方法
|
目录 1 什么是多重共线性? 2 多重共线性的影响 3 共线性的判别指标(方差膨胀因子) 3.1 拟合优度 3.2 方差膨胀因子VIF 4 多重共线性处理方法 4.1 手动移除出共线性的变量 4.2 逐步回归法 4.2.1 向前法 4.2.2 后退法 4.2.3 逐步选择法 4.2.4 检验显著性 (F 检验) 4.3 增加样本容量 4.4 岭回归 4.4.1 最小二乘法求解多元线性回归 4.4.2 岭回归处理多重共线性 4.4.3 Lasso回归处理多重共线性 4.4.4 总结 4.5 Elastic Net 4.6 主成分分析 1 什么是多重共线性?回归分析,是对两个或两个以上变量之间的相关关系进行定量研究的一种统计分析方法。我们用回归分析做需求预测,主要是发现和分析“需求”和“影响需求的因素”之间的相关关系,从而利用这些相关关系来预测未来的需求。(“需求”和“影响需求的因素”,就是回归分析面对的因变量与自变量。) 但是,在实际应用场景中,因变量和自变量存在相关关系,而自变量与自变量之间也会存在相关 关系,有时还会是强相关关系。在回归分析中,如果两个或两个以上自变量之间存在相关性,这种自变量之间的相关性,就称作多重共线性,也称作自变量间的自相关性。 我们知道在进行线性回归的时候,相比于对模型的优化,更为重要的是模型训练之前的特征工程,而剔除特征中的多重共线性对逻辑斯蒂回归而言非常重要。 多重共线性这种现象,在回归分析中普遍存在。因为: 第一,在某一时间段或某一个项目中,公司做的某一个决策,往往由很多小方案组成(比如同时采用做广告、折扣、积分返利等方式提升销量),这些小方案就是一个个的自变量,这些自变量由于是共同构成公司策略的一部分,所以可能会出现相互关联或互为补充现象,从而出现多重共线性。 第二,实际需求场景中,总会存在样本信息不充分,或者历史数据不全面和错误等情况,导致回归分析模型的参数不能准确估计与计算,从而不可避免的产生一些多重共线性。 2 多重共线性的影响多重共线性普遍存在,适度的多重共线性没有问题。但当存在严重的多重共线性时,也就是自变量之间高度相关时(相关系数R在±0.7或以上),不同自变量解释的可能是需求(因变量)的同一种变化,从而使得判定每一个单独的自变量对需求的影响程度非常困难。 也就是说,如果自变量是各自独立的变量(即不存在多重共线性),这时,根据相关分析,就能得知哪些自变量对因变量有显著影响,哪些没有影响,能很好的进行回归分析。 但是,当存在严重的多重共线性时(即各个自变量之间有很强的相关关系),自变量之间相互影响和相互变化,而我们无法固定其它自变量来避免这些影响和变化,也就无法得到这个自变量和因变量之间的真实关系。 比如,要分析自变量A对因变量的影响,自变量A与自变量B强相关。因为这自变量A与自变量B是相关的,我们分析自变量A,就需要固定自变量B,但我们无法固定自变量B,这样,就无法进行完整的分析,就无法得到我们需要的结果。 多重共线性的主要影响,在数据上表现出来为以下三个方面。 求不出回归系数a或回归系数a变得不可靠,使得回归模型失真,导致预测结果不稳定或不可靠。回归系数a正负方向不可控。即就算可以求出回归系数a,但会出现本应该出现正值的地方出现负值或者相反。判定系数R2变得不可靠或不准确。 3 共线性的判别指标(方差膨胀因子)有多种方法可以检测多重共线性,较常使用的是回归分析中的VIF值,VIF值越大,多重共线性越严重。一般认为VIF大于10时(严格是5),代表模型存在严重的共线性问题。 在了解 VIF 如何进行计算之前,需要先知道拟合优度的计算方法。 3.1 拟合优度 拟合优度测量的是线性回归中得到的模型对样本的拟合程度,使用 其中: 因此对于一个线性回归的模型来说,我们希望 y 的变化在较大程度上与 x 的变化存在相关性,因此 SSR 越大越好,并且希望随机误差对 y 的影响较小,因此 SSE 越小越好。 所以 是一个在0到1之间的值,离1越近,说明模型对样本的拟合越好。 例如我们用学习时间、读书的时间、做的题目的数量作为特征,分数作为y,做回归分析,其中books = 2倍 hours,questions = 3倍 hours ,学习到的参数有负数,但是这不符合事实,因为没有人能学习负数的时间,看负数的书,做负数的题目,考负数的考试。 我们的数据中出现了多重共线性,导致了模型的参数出现了不符合实际的参数情况。 但这是怎么造成的呢?很好理解,举个例子就明白了,考虑第一种情况,将 hours 特征设为 x1,假设我们得到的模型为: 由于 hours 和 score 之间是正相关关系,因此模型中的 w1 一定是正数。 现在,我们加入了第二个与 hours 相关性特别强的特征 books,设为 x2,我们得到的模型是: 由于 此时 x1 和 y 之间的关系没有改变,也就是说 x1 前面的参数 当然也可以: 这样就出现了参数不符合实际的情况。 那么要怎么样解决多重共线性,提高模型的可解释性呢,最直观的方法就是,把产生了多重共线性的特征直接删掉就可以了,这样做不会有太大的问题,因为当两个特征之间存在完全(近似)多重共线性,说明它们两个能够给模型提供的信息是完全(近似)一致的,而我们不需要重复信息。 方差膨胀因子(Variance Inflation Factor)是一个判断特征之间多重共线性的度量,接下来介绍VIF。 3.2 方差膨胀因子VIF我们知道,拟合优度用来衡量我们的线性回归模型是否拟合良好,它的大小不仅跟模型的好坏有关,也跟我们特征数据的分布有关,在数据分布确定的情况下,我们可以指定一个阈值,认为超过该阈值的拟合优度对应的模型就是好的模型:
然后我们发现,如果我们将特征中的一个作为我们的y(比如hours),再将其他的特征作为我们的样本数据X(比如 books, questions),然后进行拟合,如果得到的拟合优度较高,不就可以说明 y 和其他样本数据之间存在一定的多重共线性吗? 上例中,将hours作为因变量。 于是我们得到 VIF = 40.3,在习惯上,我们认为 VIF > 10 时,存在多重共线性,该特征需要删除。 除此之外,直接对自变量进行相关分析,查看相关系数和显著性也是一种判断方法。如果一个自变量和其他自变量之间的相关系数显著,则代表可能存在多重共线性问题。 4 多重共线性处理方法多重共线性是普遍存在的,通常情况下,如果共线性情况不严重(VIF 阈值,则拒绝原假设,如果 F < 阈值,则接受原假设。在计算 F 值之前,让我们先看一下如何确定这个阈值。 该阈值我们使用
而当 α 改变时,则改变了在该分布下阈值的取值: 接下来,我们计算线性模型的 F 值: 现在,线性模型的 F 值和阈值我们都已经确定,只需要两者进行对比就可以了。 4.3 增加样本容量当样本的数量较少时,多重共线性更容易出现,这是因为我们的样本都是从总体中抽样而来,可能因为各种各样的原因,也许是抽样的地域并没有覆盖所有地区,也可能是因为抽样的人群本身具备一定的特征,而导致样本数据的分布与总体的分布产生了偏差,也就是样本中数据仅是总体分布的一部分,这一部分中的特征产生了多重共线性。 比如下图中,我们可能只收集了线性相关部分的数据,而导致了样本中的多重共线性,而当数据量逐渐增加,当样本覆盖到右边的区域,会发现这两个特征之间实际上不存在太大的相关性。
但在实际情况中,继续收集数据是一项耗费时间和金钱的活,而且你也没法知道你最终收集到的数据是否真正符合总体的分布,因此这种方式也不是经常使用。 4.4 岭回归上述第1和第2种解决办法在实际研究中使用较多,但问题在于,如果实际研究中并不想剔除掉某些自变量,某些自变量很重要,不能剔除。此时可能只有岭回归最为适合了。岭回归是当前解决共线性问题最有效的解释办法。岭回归是解决共线性问题 不需要异方差自相关这些。 岭回归分析(Ridge Regression)是一种改良的最小二乘法,其通过放弃最小二乘法的无偏性,以损失部分信息为代价来寻找效果稍差但回归系数更符合实际情况的模型方程。 4.4.1 最小二乘法求解多元线性回归 多元线性回归表达式: 我们往往称上述式子为RSS(Residual Sum of Squares 残差平方和)或者SSE(Sum of Sqaured Error,误差平方和),如何求解w就用到最小二乘法:
如上述A所示,第一行和第三行存在比例关系,我们称之为精确相关关系,而B虽然不是精确相关关系,但是相差无几,只差了0.002,我们称之为高度相关关系。两种关系会导致下面的错误:
而如果是B的情况,或导致分母趋近于0,从而导致w趋近于无穷大,无法很好地拟合数据 综合上述情况为: 继续使用最小二乘法求解就会变成: 其中 Lasso回归跟上述不同,Lasso的损失函数使用L1正则化用于处理多重共线性,损失函数如下: 同样使用最小二乘法求解: 我们同样要保证X转置X的逆矩阵存在,但是Lasso回归对其没有造成任何影响,就是Lasso无法处理特征之间的精确相关关系,Lasso并没有从根本上处理多重共线性问题,只是限制了多重共线性带来的影响。 4.4.4 总结两个正则化都会压缩w的大小,会导致对标签贡献更小的特征的系数更加小,但是L2正则化只会将特征的系数尽量压缩到0,但是L1正则化主导稀疏性,会将特征系数压缩到0,这也是Lasso回归可以用于特征选择的原因。 L1正则化:会产生稀疏的权重矩阵,趋于产生少量的特征,其他特征都为0L2正则化:会选择更多的特征,但是很多的特征系数会更趋于0 4.5 Elastic NetElastic Net 是一种介于岭回归和 Lasso 回归之间的方法,其目标函数为: 主成分分析本身是一种降维方法,在面对数量较大的特征时,可以在降低维度的同时保留尽量多的信息。 简单来说,主成分分析就是将多维特征投影到较少维度的轴上,这样形成的新的特征之间一定是相互独立的,而相互独立的特征之间不存在多重共线性。 多重共线性问题,如何解决? - 知乎 解决多重共线性之岭回归分析 - 知乎 面试题解答5:特征存在多重共线性,有哪些解决方法? - 知乎 |
【本文地址】
今日新闻 |
推荐新闻 |



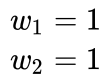
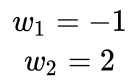

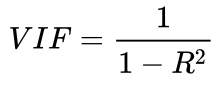




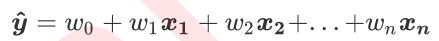 可以写成:
可以写成: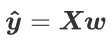 我们的目标就是求解w,如何求解w,就要用到损失函数,线性回归的损失函数为:
我们的目标就是求解w,如何求解w,就要用到损失函数,线性回归的损失函数为: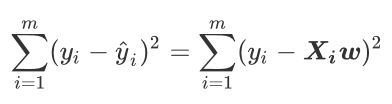 即预测值和真实值之间的差异,我们希望越小越好。
即预测值和真实值之间的差异,我们希望越小越好。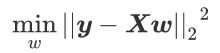

 这个时候我们要求w,就要保证上述(x转置*x)的逆矩阵存在,而逆矩阵存在的充要条件就是特征矩阵不存在多重共线性。 也就是矩阵的行列式不为0,也就是要求矩阵为满秩矩阵。
这个时候我们要求w,就要保证上述(x转置*x)的逆矩阵存在,而逆矩阵存在的充要条件就是特征矩阵不存在多重共线性。 也就是矩阵的行列式不为0,也就是要求矩阵为满秩矩阵。 




