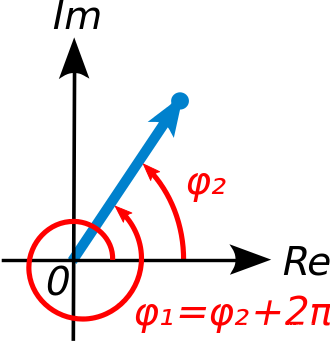以高等数学，或者更高一级的解析数学的角度看，所谓的初等函数是由 「幂函数 （power function）」「指数函数 （exponential function）」「 对数函数 （logarithmic function）」「三角函数 （trigonometric function）」「反三角函数 （inverse trigonometric function）」与常数经过有限次的有理运算（比如，加、减、乘、除、乘方、开方运算等）及有限次函数复合产生，并能用一个解析式表示的函数。

自然，复变函数的初等函数也是遵循上述规则，只不过参与演算的数从原来的实数域扩展至了复数域，于是被称为——「初等复变函数」。在大学里所涉及的复变函数的「初等复变函数」主要有四类，即指数函数、对数函数、幂函数以及三角函数。

现在我们来逐一分析。

在《复变函数 —— 0. 连接复数与三角函数的欧拉公式》 和 《复变函数 —— 1. 复数的定义》 我们分别用泰勒展开和球坐标公式，证明了重要的欧拉公式，而 欧拉公式 本身也是复变函数中极为重要的初等复变函数。

现在我们来讨论稍微一般点的情形，即如果有复函数 z = x + j y z = x + j y z=x+jy，那么可以得到

f ( z ) = e z = e x + j y = e x ( cos ⁡ y + j sin ⁡ y ) f(z) = e^z = e^{x + j y} = e^{x}( \cos y + j \sin y) f(z)=ez=ex+jy=ex(cosy+jsiny)

通常如果不特别指定，我们可以假定它的模长 ∣ e 2 k π j ∣ = ∣ e x ∣ = 1 |e^{2 k \pi j}| = |e^x| = 1 ∣e2kπj∣=∣ex∣=1，而且函数的周期是 2 k π j 2 k \pi j 2kπj。此外，指数函数有如下一些基本性质。

「arg(x)」即所谓的 幅角 函数。在数学中，它是指复数在复平面上对应的向量和正向实数轴所成的有向角。

如同在实域的「对数」是「指数」的反函数，在复数域里，也自然存在「复指数函数」的反函数「复对数函数」，因此当 e ω = z e^{\omega} = z eω=z 时，自然就有 ω = ln ⁡ z = ln ⁡ ∣ z ∣ + j arg ⁡ ( z ) \omega = \ln z = \ln |z| + j \arg(z) ω=lnz=ln∣z∣+jarg(z)。

这个没什么好再说的，所以我们直接看看一些例题。

ln ⁡ ( 1 + j ) \ln(1 + j) ln(1+j)

解：我们直接代入公式 ln ⁡ z = ln ⁡ ∣ z ∣ + j arg ⁡ ( z ) \ln z = \ln |z| + j \arg(z) lnz=ln∣z∣+jarg(z)，于是有

ln ⁡ ( 1 + j ) = ln ⁡ ∣ 1 + j ∣ + j arg ⁡ ( 1 + j ) \ln(1 + j) = \ln |1 + j| + j \arg(1 + j) ln(1+j)=ln∣1+j∣+jarg(1+j)

1 + j 1 + j 1+j 的绝对值可以通过先转换为复平面向量，再求模长的方式得到，于是：

∣ 1 + j ∣ ⇒ ( 1 , 1 j ) ⇒ 1 2 + 1 2 = 2 |1 + j| \Rightarrow (1, 1j) \Rightarrow \sqrt{1^2 + 1^2} = \sqrt{2} ∣1+j∣⇒(1,1j)⇒12+12 ​=2 ​

然后关于幅角 arg ⁡ ( 1 + j ) \arg(1 + j) arg(1+j)，又要怎么处理呢，首先它的实轴长度为1，虚轴长度为1，即 x > 0 x>0 x>0， y > 0 y>0 y>0，根据弧角与arctan函数之间的关系，

arg ⁡ z = { arctan ⁡ y x x > 0 π 2 x = 0 ,   y > 0 − π 2 x = 0 ,   y < 0 arctan ⁡ y x + π x < 0 ,   y ≥ 0 arctan ⁡ y x − π x < 0 ,   y < 0 \arg z = \left \{ \begin{matrix} \arctan \frac{y}{x} & x > 0 \\ \\ \frac{\pi}{2} & x = 0, \ y> 0 \\ \\ -\frac{\pi}{2} & x = 0, \ y < 0 \\ \\ \arctan \frac{y}{x} + \pi & x < 0, \ y \ge 0 \\ \\ \arctan \frac{y}{x} - \pi & x < 0, \ y < 0 \end{matrix} \right. argz=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​arctanxy​2π​−2π​arctanxy​+πarctanxy​−π​x>0x=0, y>0x=0, y