该算法可以搜索无负权环的带权有向图的单源节点到其他节点的所有最短路径。我们先介绍一个预备概念路径松弛（relaxtion）。大多数图的搜索都是通过不断迭代，不断的进行路径松弛得到最中的最优结果的

在图的搜索中，我们通常在每个节点上保存一个 v.d (v为节点标识)的属性，在搜索的过程中用来记录源节点到当前节点的最短路径权重的上界，这个上界又称之为最短路径估计；以及保存一个 v.\pi 属性， v.\pi 来保存节点所在的当前搜索到的最短路径上的前驱节点信息。我们通过下面这个简单的图，看一下这个 v.d 的计算方式

上图中圆圈内部的值代表v.d的值，其中节点的搜索过程为 S\rightarrow A \rightarrow C\rightarrow A \rightarrow B ，S为源节点，源节点的由于是搜索的起始节点，所以该节点对应的v.d为0，C节点的C.d为1是S节点的 S.d+w(S,C) 的结果，其中 w(S,C) 为节点S到C的边的权值

可能细心的朋友会发现，上图中节点A的v.d不应该是3吗？即S节点的 v.d+w(S,A)=3 。这里面就引入了路径松弛的操作了。

引用《算法导论》里面的一句话

我们带着上面的描述重新回到，我们先从源节点S出发，计算邻接节点A和C的最短路径估计值，分别对应 A.d=3 、 C.d=1 ，然后我们再根据 S \rightarrow C 的这条路径往下计算得到 A.d=C.d+w(C,A)=1+1=2 ，很明显这个最短路径的估计值小于之前的最小路径估计值3。所以这里根据松弛操作，对A.d进行更新，更新为2

上面就是这个松弛操作的过程描述，下面我们来仔细品一下其中的几个名词

最短路径估计，在搜索的过程中得到的v.d被称之为最短路径估计。这个估计这个词用的非常好，估计就是不确定的意思，也就是说这里得到的最短路径的长度是基于当前搜索状态（当前对于图的部分搜索所得到的信息）得到的值，当前得到的信息对于整个图的信息是不全面的（因为还没有对整个图的信息进行全面的搜索抉择），所以这里的值是估计的是基于当前得到的图的部分信息所计算出来的值，可能不是最优值。

开篇提到的最短路径的上界在搜索的过程中也称之为最小路径估计，这里的上界表现在，在搜索过程中得到的最短路径的估计值是非递增的，如果找到更小的最小路径估计就更新，如果相等或者更大就不更新。所以，得到的最短路径的估计是当前以及后续阶段的最大值即上界

图索搜中松弛操作非常关键，在图的搜索过程中，不断的对每个边进行松弛操作。一步一步的基于图的信息对所有的路径预估值进行更新操作，在最终搜索完成的时候得到最优的值

路径松弛对应的伪代码如下：

上面的伪代码是基于E(u,v)进行松弛操作，用来更新v对应的 s\rightsquigarrow v 的预估值v.d。w(u,v)对应的是E(u,v)的权值。另外 v.pi 同 v.\pi

本文中介绍的两种图搜索算法都用到了松弛操作，只不过使用情况不同

下面，我们直接贴出伪代码，通过伪代码了解计算过程

代码行中最后一个for循环是用来检测是否有负权环的，工作过程以及原理我们先按下不表。先多说一句，Bellman-Ford是无法对于含有负权环的有向带权图进行搜索的，所以这里面检测到负权环的时候，函数返回FALSE用来表示发现负权环，搜索失败

该算法运用的思想是对于所有边进行|G.V｜-1次松弛，每次基于所有边进行松弛操作。然后执行这个操作|G.E|-1次。最终执行完成之后，算法在搜索过程就算终止了，得到了最终的结果（在没有负权环的情况下，当前图中节点中包含的最小路径估计以及前驱节点就是最优解）

补充说明，负权环图就是对组成这个环的所有的边的权值进行累加，得到的最终累加权值为负数，则这个环称之为负权环，示例负权环如下图中的绿色底的部分所示

上面代码中函数开始的第一行，调用了一个INITIALIZE-SIGNAL-SOURCE函数，该函数是是用来在进行搜索前的初始化的。其作用是用来将所有节点的 v.\pi 属性初始化成NIL即空的状态，表明这些节点还没有搜索到最短路径上的前驱节点；并且源节点的s.d初始化成0以及将其他节点（ v \in V - {S} ）的v.d初始化成 \infty ，表明初始化中没有最短路径。具体为代码如下

伪代码中 v.pi 同 v.\pi 这里我们通过如下图中示例，来对算法的计算过程进行举例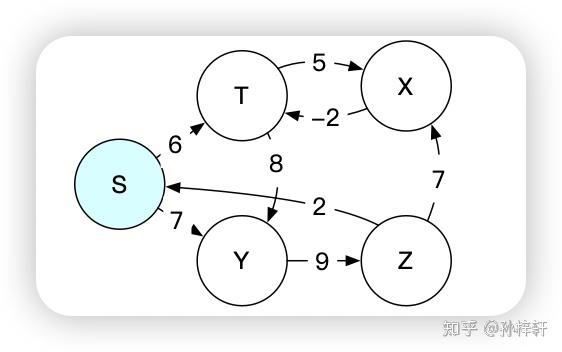

图的结构如上图所示，蓝色底的S节点是源节点，我们约定该图的所有节点的边存储顺序如下

基于上面的边的存储顺序，算法计算过程可视化如下图所示

上图中分为两个部分，上边那一行时依据图的结构来进行搜索过程的展示，其中圆圈内部代表的是这个节点的最短路径估计值v.d，其中infty代表 \infty ，用来表示该节点当前没有有效的最短路径估计（即未发现源节点到该节点的可达路径）。图中实线箭头代表节点之间的有向边，实线上的数值代表该边的权值。图中虚线代表当前最小路径估计下的前驱节点，即 v.\pi

下边那一行，是用搜索树的形式对搜索过程进行展示，其中圆圈内代表这个节点的最短路径估计值v.d，这个是和上边依据图结构进行展示的说明是一致的。搜索树的根节点是源节点S，树边代表的是前驱节信息 v.\pi 。值得注意的是，如果搜索过程中最短路径估计为 \infty 的节点在搜索树中是没有展示的，因为这些节点其和源节点之间没有可达路径，所以其没有前驱节点，即没有树边和源节点进行关联，所以在树中进行展示

上图中绿色底代表的编号是对应的第几次对所有的边完成松弛操作之后的状态，上图中展示了两次对与所有边进行松弛操作之后的状态，3和4没有进行展示，因为3和4是和2是相同的状态

我们在这里主要讨论几个关键的步骤，先讨论上边0.5步到1步的过程

在搜索到0.5步的时候，对应下边的搜索树中的第二个树，我们可以看出当前Y的最短路径估计是15，这个最短路径估计值是居于节点T计算出来的，并且此时第一次对所有边的松弛操作还没有完全完成（主要是还没有松弛到边E(S,Y)）。所以在这一步的Y的前驱节点是T，程序继续运行，当对边E(S,Y)进行路径松弛之后发现，得到的新的最短路径估计值为7，是小于原来的15的。所以更新最短路径估计并且更新其前驱节点为S。这个过程对应搜索树中就好像，将搜索树1中虚线框的分支剪掉，更新Y节点的最小路径估计，并且将其接到S节点的后边，成为S节点的子分支

之所以会出现剪枝的情况，这也恰巧和搜索过程是一个迭代的过程，并且在迭代的过程中，最短路径估计上图中最短路径的上界的说法不谋而合，在算法的中间状态，得到的路径不一定是最短路径，其中间某一个状态得到的最短路径仅仅是当前搜索到的可达路径中的最短路径，所以这也体现了该算法是在循环中对图不断的向前试探收集更新当前信息的过程

细心的朋友可能会发现，上图中第三棵搜索树和第一行步骤1中的Z节点的最短路径估计值是24，这个最短路径估计值是基于剪枝之前Y的最短路径估计值为15计算的，在进行剪枝转接的过程，并没有对Z节点的最短路径估计值进行更新。虽然在当前状态下Z的路径估计值是不正确的，但是这个最短路径估计值会在后续的松弛过程进行正确的更新

从上面算法中我们可以看出来v.d在算法迭代的过程中，会被不断的计算调整，不断的尝试朝更小的数值进行调整更新。但是随着算法的推进，这个数值是有下界的，即 v.d\geq \delta(s,v) （该定理也被称之为上界定理，这里面的上界可以理解为每次得到的v.d在后续的所有松弛操作中得到的v.d值的集合中是最大的，是上界限）。当v.d= \delta(s,v) 的时候，该节点的最短路径值就已经得到，在后续的算法执行过程中，该值不会被更新了稳定了（这块有个最短路径的收敛性质作为支撑）。即v.d收敛到 \delta(s,v) 了，这里面的 \delta(s,v) 代表从s节点到v节点的最短路径值

上图中，在算法运行到得到步骤2的状态的时候，其实就可以得到最终的结果了，后续的运算看起来像是浪费了。其实不是这样的，算法对所有边松弛一遍的这个过程执行多少次能得到最终的结果，其实取决于图的结构和边的松弛顺序（边的松弛顺序就是边的存储顺序，因为算法是对边的存储集合进行从前到后的按照存储顺序进行松弛操作的）

Bellman-Ford是一个对于无负权环的带权有向图进行搜索的通用性的算法，其内部将依次对所有边进行松弛操作执行了|G.V|-1，是基于最差的情况考虑的。最多需要|G.V|-1次，在经过过这些次之后，得到的结果一定是最优的

从上图中搜索树的变化，我们可以看出随着搜索的过程，每进行一次所有边的松弛操作之后，搜索树都会有一个新的节点到源路径的最短路径是被确认的。我们依然以上图搜索过程为例子，根据搜索树做出如下图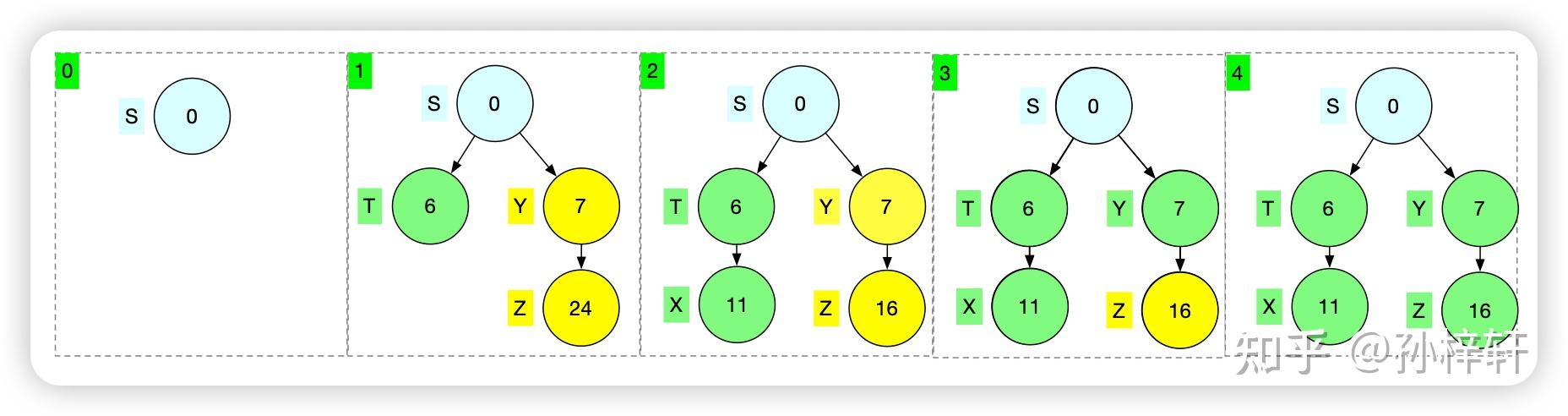

上图中绿色底色的序号依然代表第几次对于所有边进行松弛操作之后的状态，其中每个格子中的搜索树中绿色的点代表已经确定到源节点S的最短路径以及最短路径值。从图中可以看出，每经历一次对所有的边的松弛操作之后，就可以增加一个绿色节点。黄色节点表示该节点虽然有最小路径估计值，但是不确定该最小路径估计值是不是最短路径值，即该点是存疑的

下面我们考虑一下，为什么每经历一次松弛操作都可以确定一个点的最短路径估计。考虑下图中的几种情况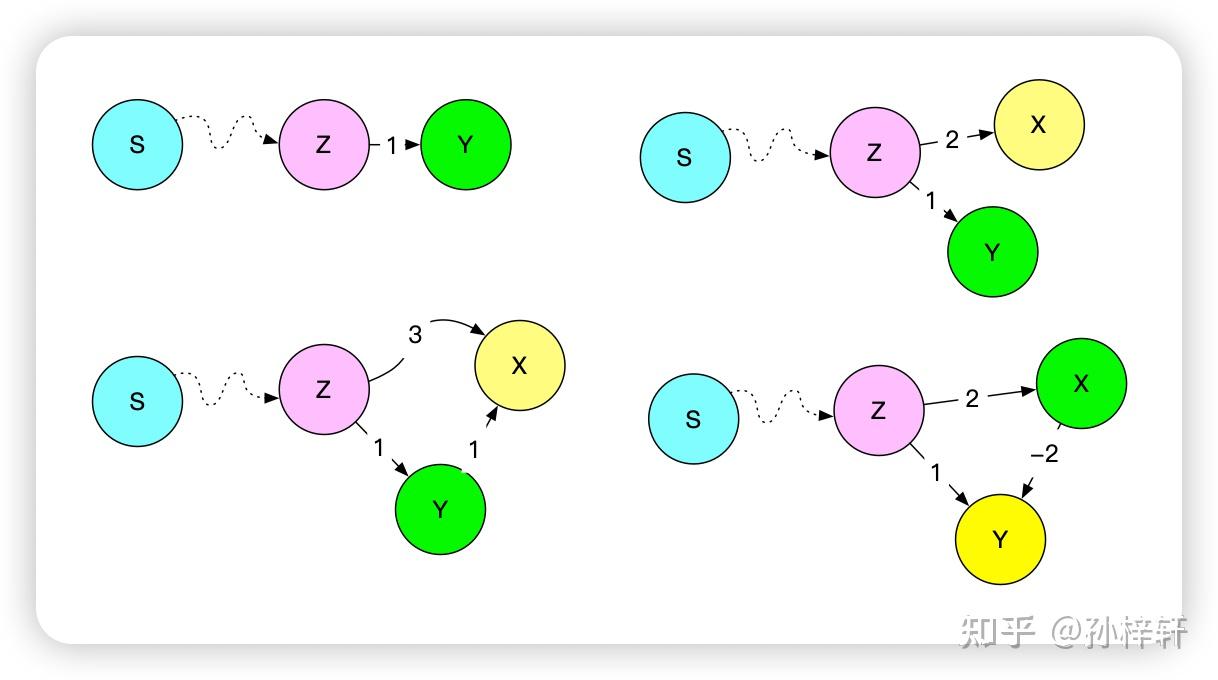

考虑一般性，我们选择一个图中已经确定得到最短路径值的一个点Z即 Z.d=\delta(S,Z) 。上图展现了四种情况，其中绿色底的就是在Z得到最短路径估计值的那次松弛过程的下一次松弛过程中得到最短路径估计值的Z的子节点。从上图中可以看出前3个图（图的顺序约定为从左到右从上到下）中绿色底的节点所在的边是Z所有出边中权值最小的出边。而第4中的节点所在的边则不是权值最小的出边，这是因为Z经过X到达Y的这条路更近，所以在第4中情况最短路径估计值确定的点就是X

你可能会想，比如第4张图中，如果存在另外一个路径（不经过节点Z）的路径，也可以到达X，并且这条路径更短，那么X当前计算出来的最短路径估计不就不是最小的了吗？就比如下边这种情况

确实是这样的，在基于局部的搜索状态信息，在算法未运行到最后的时候，确实很难基于当前的状态，指定出来某一个节点的当前的 v.d 中是否已经是最优的。但是算法是不断迭代的，无论在什么图中，我们总可以在当前的所有的已经得到最短路径值的节点的所有出边的终止节点中找到一个点，这个点的最短路径是来源于其该出边对应的起始节点的，那么对该边进行一次松弛操作之后，该边的终止节点的最短路径值就被确认了（总可以找到像前四种情况那样的Z节点的子节点没有其他不经过的Z节点的更短的路径到达该节点）

上图中的几种情况说明了，每一次对所有边进行松弛操作之后，总会有一个节点最短路径值被确定，即 v.d 收敛到了 \delta(s,v) 。实际在真实的搜索过程中，每一次松弛操作至少确认一个节点的最短路径值，这里面为什么有一个至少的这个修饰，说明也可以在一次对于所有边的松弛操作确认多个节点的最短路径值。这主要取决于图的结构和存储方式，下面我们举例说明

上面的图的结构比较简单，就是一个简单的线性展开的单链的图，由于每一个节点只有一个出边和一个入边。并且边的存储输出为G.E={E(Z,T),E(Y,Z),E(X,Y),E(S,X)}。所以每次基于所有的边进行路径估计值计算的时候，只能将一个 \infty 更新成实数，所以需要最多|G.V|-1次可以将所有的 \infty 更新成实数。当然，这里面讨论的是连通图，对于非连通图在经历了|G.V|-1次更新之后，剩余的搜有的v.d为 \infty 的点都是源节点出发的路径无法到达的点，在继续更新下去也是一样的

上面举例的这个图，是一个特殊情况，在一般性的无负权环图的有向带权图中，最多需要|G.V|-1次就可以得到最终的结果。至于最少需要多少步所有边的松弛可以得到最优的结果，取决于边的存储顺序以及图的结构，比如上边的存储过程如果变成G.E={E(S,X),E(X,Y),E(Y,Z),E(Z,T)}（将上面边的顺序反向一下）则可以在第一次对所有边进行松弛操作完成之后就可以得到最优的结果

某些满足某些约束条件的图，可以对图的结构进行按照某种规则的排序，这样可以对所有边进行一次松弛操作就可以得到最终最优的结果。提升算法效率，比如DAG算法（松弛操作的顺序对于图的搜索很重要，后续会以DAG算法为例对这个问题进行讲解）

总结一下，该算法为什么可以在算法终止的时候得到最优的结果

Bellman-Ford就这样在迭代的过程中，不断的计算并且收敛 v.d ，沿着S节点为中心向外辐射的方向稳扎稳打的逐步推进求解

经过以上讨论，我们已经对Bellman-Ford算法的运行过程和运行原理有了基本的了解，下面我们思考一个问题：为什么Bellman-Ford处理不了带负权环的有向带权图？

我们用下图为示例，考虑如下这三个路径 1\rightarrow2\rightarrow3\rightarrow4 以及 1\rightarrow2\rightarrow3\rightarrow5\rightarrow2\rightarrow3\rightarrow4 和 1\rightarrow2\rightarrow3\rightarrow5\rightarrow2\rightarrow3\rightarrow5\rightarrow2\rightarrow3\rightarrow4 ，这三个路段的路径权值是依次递减的。这是因为 2\rightarrow3\rightarrow5\rightarrow2 这个环路的路径权值为负，也就是说在这个环路总绕的圈越多，得到的路径权值就越小。这样就会有无限个依次递减的路径，永远无法找到那个最短的路径

所以在有负环存在的有向带权图，如果源节点S和节点V之间，如果存在一条可达路径经过负权环的时候，那么这两个节点之间就不存在最短路径

假设边的存储顺序为：G.V={E(S,X),E(X,Y),E(Y,Z),E(Y,T),E(T,X)}，在Bellman-Ford算法中每一次基于所有边进行松弛的时候，其松弛的顺序和边的存储顺序是对应的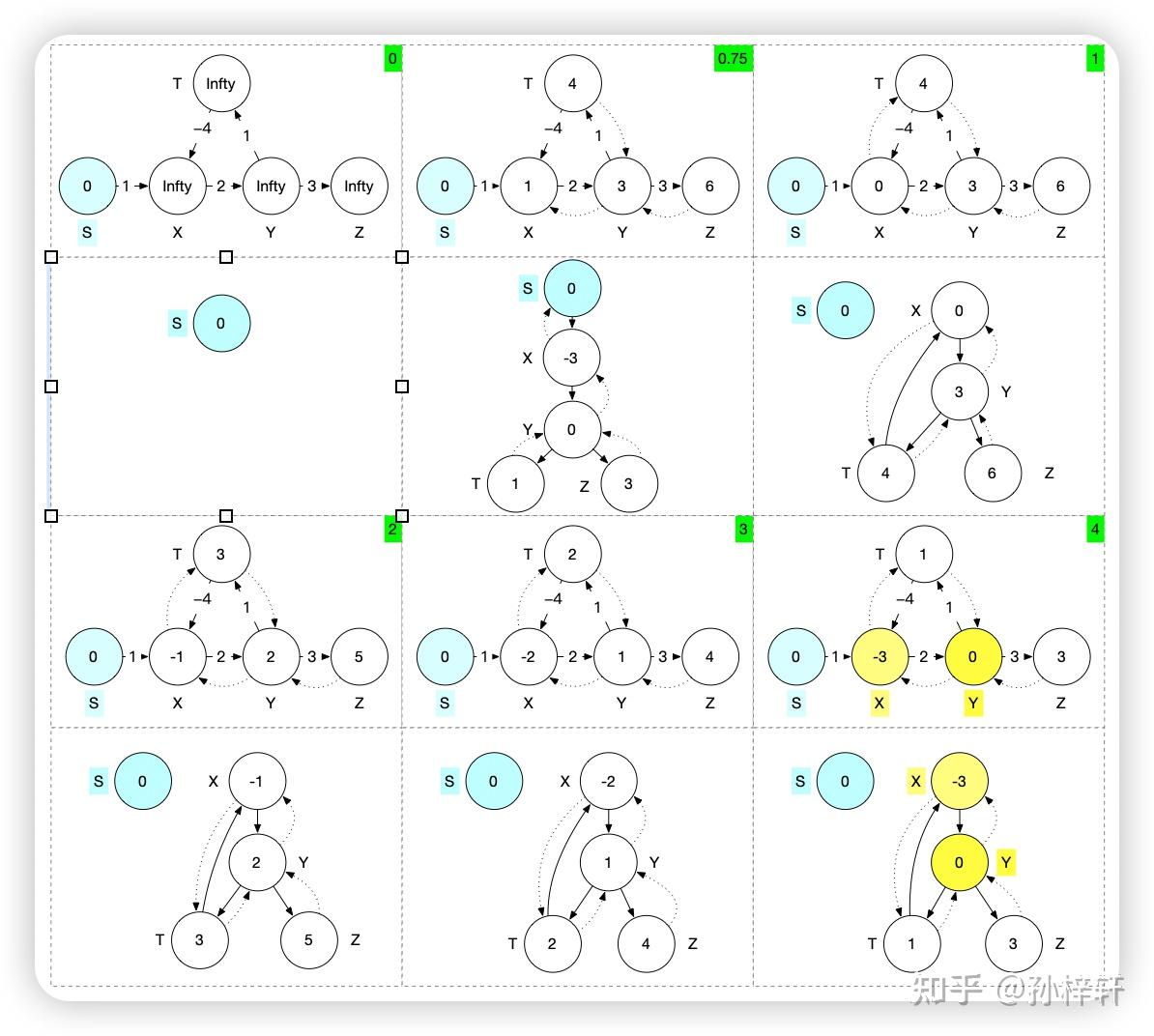

上图中展示了图在搜索迭代过程中的状态，通过两种方式来展示，分别为上边的通过图的结构来展示算法的执行过程，下面对应的是通过搜索树的形式来展示执行过程。其中圆圈中的数字就是v.d，其中Infty代表的是 \infty 。虚线指定了当前点的当前v.d值对应的路径上的前驱节点信息，即 v.\pi 信息。

上图中绿色底代表的是第几次对所有边进行路径松弛操作，其中0.75代表的是第1次对所有的边进行的松弛操作进行了部分，还有部分边没有进行路径松弛操作

上图中第4步中的负权环中的边E(T,X)是在该负权环中的所有边中最后被松弛的，而Y节点的最短路径估计是基于E(T,X)被松弛前的X的最短路径估计来进行计算的。所以当程序结束循环的时候，对于负权环总有一个点的最短路径估计值被最后进行更新，并且是有效更新（这里的有效指的是v.d的值被更改成更小的值），这个时候其他环上的其他点的最短路径估计值是一个过期的值，从这个角度上来看，有负权环的图是无法通过Bellman-Ford来计算的

上面我们是根据v.d来对算法无法处理带负权环的图的分析，下面我们基于另外一个关键的数据结构 v.\pi 来进行分析

从0.75步到1步，我们可以看出X节点和S节点之间的联系（前驱关系）在第1步的时候断了，这是因为经历了一次负权环的松弛之后，得到的X.d的值小于原来基于 S.d+w(S,X) 的值了，所以被更新了。这导致了X和S之间的路径的线断了。并且这条线在后续的迭代过程中不会得到修复，这是由于因为负权环的存在，X.d已经没有下界了在后续的迭代过程中这个值会不断的减小，永远都小于 S.d+w(S,X) 。

S节点和X节点之间的线断开了之后，算法结束之后就无法通过前驱信息（ v.\pi ）来反推出S节点到X节点之间的路径了

最后，我们探讨一下上述Bellman-Ford的最后一个循环，该循环是用来检测图中是否有负权环的，如果有负权环程序返回FALSE。告诉调用方，图中含有负权环图搜索失败

伪代码中通过对所有进行一次遍历，判定E(u,v)中的v节点的最短路径值v.d是不是大于当前最短路径估计u.d+w(u,v)。如果大于则说明图中存在负权环

上图中其实是基于上界性质来进行检测的，三角不等式（Triangle inequality）的定义如下

三角定理，从名字上就可以看出和三角形相关，可以通过如下图示来理解，下图中的delta同 \delta

上面我们证明过了，在没有负权环的图中，最中得到的所有节点的最短路径估计 v.d=\delta(s,v) 。带入到三角不等式公式中，最中得到的应该是 v.d \leq \delta(s,u) + w(u,v) ，所以当对于所有边进行测试的时候，如果存在 v.d > u.d+w(u,v) 的时候，不满足前面公式了，则说明存在负权环了

你可能会有疑惑，为什么 v.d > u.d+w(u,v) 情况存在的时候，就一定是负权环导致的。首先，我们证明过在无负权环的其他情况中，是一定不会发生这种情况的，所以排除法，如果存在这种情况，那么就一定是负权环导致的

最后，详细可以参考《算法导论》这个书籍，我是参考的《算法导论第3版》。这个书不错，推荐枕边常备