利用主成分PCA进行特征提取 |
您所在的位置:网站首页 › 基于pca特征选择与特征提取 › 利用主成分PCA进行特征提取 |
利用主成分PCA进行特征提取
|
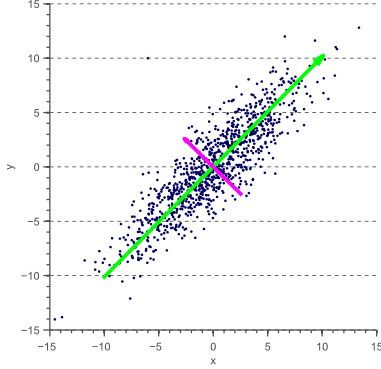
本文将介绍主成分分析(Principal Component Analysis,PCA)原理,并且它如何在分类问题中发挥降维的作用。译自 Feature extraction using PCA。 简介本文将介绍主成分分析(Principal Component Analysis,PCA)原理,并且它如何在分类问题中发挥降维的作用。 在前面我们讲到过维度灾难,分类器容易对高维的训练集产生过拟合。那么,哪些特征是更好的呢,而哪些又该从高维中除去呢 如果所有的特征向量间相互独立,我们可以很容易的去除区分度很小的特征向量,区分度小的向量可通过特征选择相关方法识别。然而,在实际中,很多向量彼此依赖或依赖潜在的未知变量。一个单一的特征可以用一个值来代表很多信息的集合。移除这样的特征将移除比所需要的更多的信息。在下一节,我们将介绍作为特征提取的解决此问题的PCA方法,并从两个不同的角度介绍它的内在工作原理。 PCA:一种去相关方法屡见不鲜的是,特征都是相关的。例如,我们想要使用图像中每个像素的红色,绿色和蓝色分量来进行图像分类(例如侦测猫和狗),对红光最敏感的图像传感器也捕获一些蓝光和绿光。 类似地,对蓝光和绿光最敏感的传感器也对红光表现出一定程度的敏感度。 结果,像素的R,G,B分量在统计上是相关的。因此,简单地从特征向量中消除R分量,也隐含地除去关于G和B信道的信息。换句话说,在消除特征之前,我们想要转换完整的特征空间,从而得到底层的不相关分量。 下图是一个二维特征空间的例子:
图中的特征x和y明显是相关的。事实上,它们的协方差矩阵是:
在前面的文章中,我们讨论了协方差矩阵的几何解释。 我们看到,协方差矩阵可以分解为在白色的不相关数据上一系列旋转和缩放操作,其中旋转矩阵由该协方差矩阵的特征向量定义。 因此,直观地看到,通过旋转每个数据点,上图所示的数据D可以被解相关,使得特征向量V成为新的参考轴:
经旋转缩放的数据的协方差矩阵现在是对角线的,这意味着新的轴是不相关的:
事实上,上上图中的原始数据是通过两个1维高斯特征向量x1 ~ N(0,1),x2 ~ N(0,1)的线性组合生成的:
因为特征x和y是x1和x2的一些未知的潜在成分的线性组合,直接去除x或y的任意一个,都将丢失来自x1和x2的一些信息。而将数据协方差的特征向量进行旋转,会使我们直接恢复这两个独立的成分x1和x2(达到比例因子)。这可以被看作如下:原始数据的协方差矩阵的特征向量是(每列代表一个特征向量):
首先要注意的是,在这种情况下,V是一个旋转矩阵,对应于45度旋转(cos(45)= 0.7071),从图1中确实可以看出。其次,将V视为在新的坐标系中线性变换矩阵结果 ,每个新的特征x'和y'被表示为原始特征x和y的线性组合:
换句话说,特征空间的去相关对应于数据的未知不相关组件x_1和y_1的恢复(如果变换矩阵不是正交的,则恢复到未知缩放因子)。 一旦这些组件被恢复,通过简单地消除x_1或x_2就很容易降低特征空间的维度。 在上面的例子中,我们从一个二维问题开始。 如果我们想要降低维数,问题依然是消除x_1(从而x')还是y_1(从而y')。 尽管这种选择可能取决于许多因素,例如在分类问题的情况下数据的可分性,但PCA只是假设最有意思的特征是具有最大差异或差异的特征。 这个假设是基于信息理论的观点,因为具有最大方差的维度对应于具有最大熵的维度,因此编码最多的信息。 最小的特征向量通常会简单地表示噪声分量,而最大的特征向量通常对应于定义数据的主要分量。 然后简单地通过将数据投影到其协方差矩阵的最大特征向量上来实现通过PCA的降维。 对于上面的例子,所得到的一维特征空间如图3所示:
显然,上面的例子很容易推广到更高维的特征空间。 例如,在三维情况下,我们可以将数据投影到由两个最大特征向量所定义的平面上以获得二维特征空间,或者我们可以将其投影到最大特征向量上以获得一维特征空间。 如图4所示:
一般来说,PCA允许我们获得原始N维数据的线性M维子空间,其中M |
【本文地址】
今日新闻 |
推荐新闻 |
 图一
图一

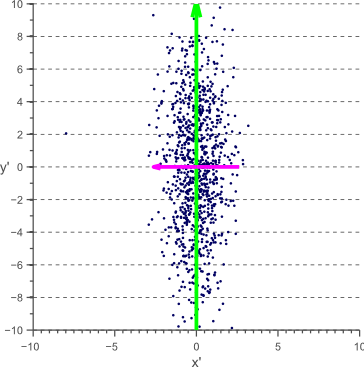 图2
图2
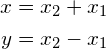
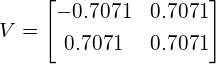
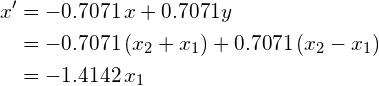
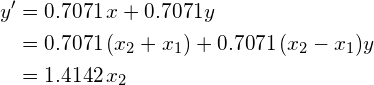
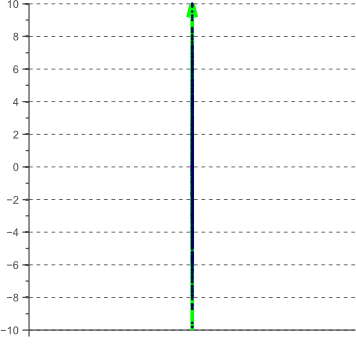 图3
图3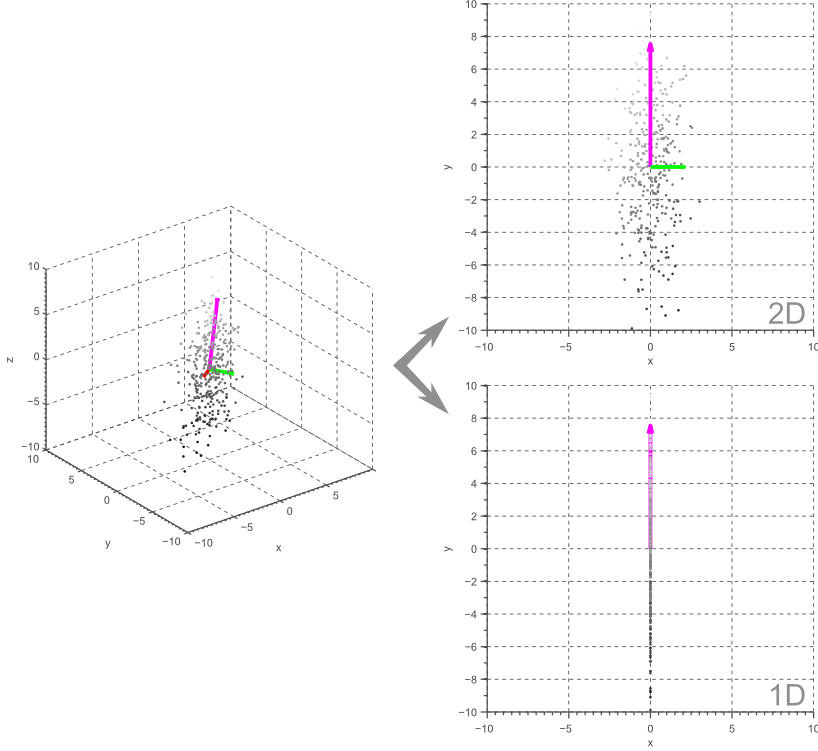 图4
图4