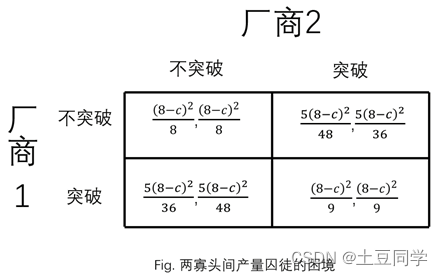
连续产量古诺模型，又称古诺双寡头模型 (Cournot duopoly model)，或双寡头模型 (Duopoly model)是博弈论中非常经典的模型，以两厂商连续产量古诺博弈为例：

Player：两个供应相同产品的厂商

产量：厂商1的产量为q1，厂商2的产量为q2，市场总供给为Q=q1+q2。

市场出清价格P：市场总供给的函数P(Q)=8-Q (市场出清价格是可以将产品全部卖出的价格)

成本：设两个厂商都无固定成本，每增加一单位产量的边际成本c1=c2=c。

最后强调两个厂商同时决策,即决策之前都不知道另一方产量(完全信息静态博弈)。

该博弈两博弈方的策略空间是他们可以选择的产量。假设产量是连续变量，也就是说两厂商有无限多种可选策略。两博弈方的得益是两个厂商各自的利润，即各自的销售收益减去各自的成本： π 1 = q 1 P ( Q ) − q 1 c = q 1 ( 8 − ( q 1 + q 2 ) ) − c q 1 = − q 1 2 − c q 1 − q 1 q 2 + 8 q 1 π_1=q_1 P(Q)-q_1 c=q_1 (8-(q_1+q_2 ))-cq_1=-q_1^2-cq_1-q_1 q_2+8q_1 π1​=q1​P(Q)−q1​c=q1​(8−(q1​+q2​))−cq1​=−q12​−cq1​−q1​q2​+8q1​ 和 π 2 = q 2 P ( Q ) − q 2 c = q 2 ( 8 − ( q 1 + q 2 ) ) − c q 2 = − q 2 2 − c q 2 − q 1 q 2 + 8 q 2 π_2=q_2 P(Q)-q_2 c=q_2 (8-(q_1+q_2 ))-cq_2=-q_2^2-cq_2-q_1 q_2+8q_2 π2​=q2​P(Q)−q2​c=q2​(8−(q1​+q2​))−cq2​=−q22​−cq2​−q1​q2​+8q2​ 其中， π 1 π_1 π1​、 π 2 π_2 π2​分别是厂商1、厂商2的利润。可以看出，两博弈方的得益都取决于双方的产量。这个博弈中，我们需要找到纳什均衡，即只要策略组合 ( q 1 ∗ , q 2 ∗ ) (q_1^*,q_2^*) (q1∗​,q2∗​)满足 q 1 ∗ q_1^* q1∗​和 q 2 ∗ q_2^* q2∗​相互是对于对方的最佳对策就构成纳什均衡。

根据纳什均衡的定义知道,纳什均衡就是相互是最优对策的各博弈方策略组合。因此,如果策略组合 ( q 1 ∗ , q 2 ∗ ) (q_1^*,q_2^*) (q1∗​,q2∗​)是本博弈的纳什均衡,就必须是下列最大值问题的解： { m a x q 1 ⁡ ( − q 1 2 − c q 1 − q 1 q 2 ∗ + 8 q 1 ) m a x q 2 ⁡ ( − q 2 2 − c q 2 − q 1 ∗ q 2 + 8 q 2 ) \begin{cases} \underset{q_1}{max}⁡(-q_1^2-cq_1-q_1 q_2^*+8q_1)\\ \underset{q_2}{max}⁡(-q_2^2-cq_2-q_1^* q_2+8q_2) \end{cases} ⎩ ⎨ ⎧​q1​max​⁡(−q12​−cq1​−q1​q2∗​+8q1​)q2​max​⁡(−q22​−cq2​−q1∗​q2​+8q2​)​

上述两个求最大值的式子都是各自变量的二次式,且二次项系数都小于0,因此只要 q 1 ∗ q_1^* q1∗​和 q 2 ∗ q_2^* q2∗​能使两式各自对 q 1 q_1 q1​和 q 2 q_2 q2​的导数为0就能实现两式的最大值。

即令 { − 2 q 1 − c − q 2 ∗ + 8 = 0 − 2 q 2 − c − q 1 ∗ + 8 = 0 \begin{cases} -2q_1-c-q_2^*+8=0\\ -2q_2-c-q_1^*+8=0 \end{cases} {−2q1​−c−q2∗​+8=0−2q2​−c−q1∗​+8=0​

又因为策略组合 ( q 1 ∗ , q 2 ∗ ) (q_1^*,q_2^*) (q1∗​,q2∗​)是本博弈的纳什均衡，故解下列方程 { − 2 q 1 ∗ − c − q 2 ∗ + 8 = 0 − 2 q 2 ∗ − c − q 1 ∗ + 8 = 0 \begin{cases} -2q_1^*-c-q_2^*+8=0\\ -2q_2^*-c-q_1^*+8=0 \end{cases} {−2q1∗​−c−q2∗​+8=0−2q2∗​−c−q1∗​+8=0​

得到方程组唯一解: { q 1 ∗ = 8 − c 3 q 2 ∗ = 8 − c 3 \begin{cases} q_1^*=\frac {8-c}{3}\\ q_2^*=\frac {8-c}{3} \end{cases} {q1∗​=38−c​q2∗​=38−c​​

可以进一步得到市场总供给 Q = q 1 ∗ + q 2 ∗ = 16 − 2 c 3 Q=q_1^*+q_2^*=\frac {16-2c}{3} Q=q1∗​+q2∗​=316−2c​ 市场出清价格为 P = 8 − ( 16 − 2 c ) / 3 = 8 + 2 c 3 P=8-(16-2c)/3=\frac {8+2c}{3} P=8−(16−2c)/3=38+2c​ 故双方的得益分别为: π 1 = q 1 ∗ P ( Q ) − q 1 ∗ c = 8 − c 3 ∙ ( 8 + 2 c 3 − c ) = ( 8 − c ) 2 9 π_1=q_1^* P(Q)-q_1^* c=\frac {8-c}{3}∙(\frac {8+2c}{3}-c)=\frac{(8-c)^2}{9} π1​=q1∗​P(Q)−q1∗​c=38−c​∙(38+2c​−c)=9(8−c)2​ π 2 = q 2 ∗ P ( Q ) − q 2 ∗ c = 8 − c 3 ∙ ( 8 + 2 c 3 − c ) = ( 8 − c ) 2 9 π_2=q_2^* P(Q)-q_2^* c=\frac {8-c}{3}∙(\frac {8+2c}{3}-c)=\frac{(8-c)^2}{9} π2​=q2∗​P(Q)−q2∗​c=38−c​∙(38+2c​−c)=9(8−c)2​ 总收益为(s为separate)： π s ∗ = π 1 + π 2 = 2 ( 8 − c ) 2 9 π_s^*=π_1+π_2=\frac{2(8-c)^2}{9} πs∗​=π1​+π2​=92(8−c)2​ π s ∗ π_s^* πs∗​为两个厂商在各自做决策场景下的总收益。

如果从两个厂商总体利益最大化角度进行统一的产量选择,就要求实现两个厂商总和利润最大的总产量。设总产量为Q,则总利润为 π o = Q P ( Q ) − c Q = Q ( 8 − Q ) − c Q = − Q 2 + ( 8 − c ) Q π_o=QP(Q)-cQ=Q(8-Q)-cQ=-Q^2+(8-c)Q πo​=QP(Q)−cQ=Q(8−Q)−cQ=−Q2+(8−c)Q 其中 π o π_o πo​(o为overall)为两个厂商总体决策时的总利润，则同样求一阶导得到当 Q = ( 8 − c ) / 2 Q=(8-c)/2 Q=(8−c)/2时，取得最大值 π o ∗ = ( 8 − c ) 2 4 π_o^*=\frac {(8-c)^2}{4} πo∗​=4(8−c)2​

将两个厂商进行统一的产量选择时的结果与两个厂商独立决策、追求各自利润最大化时的博弈结果相比: π ∗ = { 2 ( 8 − c ) 2 9 ， Q ∗ = ( 16 − 2 c ) 3 ( 8 − c ) 2 4 ， Q ∗ = ( 8 − c ) 2 π^*= \begin{cases} \frac{2(8-c)^2}{9}， Q^*=\frac {(16-2c)}{3} \\ \frac {(8-c)^2}{4} ， Q^*=\frac {(8-c)}{2}\\ \end{cases} π∗={92(8−c)2​，Q∗=3(16−2c)​4(8−c)2​，Q∗=2(8−c)​​

不难发现，从两个厂商总体利益最大化角度进行统一的产量选择时，总产量较小,而总利润却较高。

因此从两个厂商的总体来看,根据总体利益最大化决策效率更高，即如果两个厂商联合起来决定产量,先定出使总利益最大的总产量( 8 − c 2 \frac {8-c}{2} 28−c​)后各自生产其一半( 8 − c 4 \frac {8-c}{4} 48−c​),则各自可分享到单位利润 ( 8 − c ) 2 8 \frac {(8-c)^2}{8} 8(8−c)2​,比各自独立决策获得的利润 ( 8 − c ) 2 9 \frac {(8-c)^2}{9} 9(8−c)2​要高。

当然,在两个独立决策的企业之间实现合作并不容易。合作难以实现的原因主要是合作的产量组合( 8 − c 4 \frac {8-c}{4} 48−c​, 8 − c 4 \frac {8-c}{4} 48−c​)不是纳什均衡。在这个策略组合中，双方都可以独自改变自己的策略得到更高的利润,双方都有突破 8 − c 4 \frac {8-c}{4} 48−c​单位产量的冲动。在缺乏有强制性协议保障的情况下,这种冲动注定了不可能维持产量组合( 8 − c 4 \frac {8-c}{4} 48−c​, 8 − c 4 \frac {8-c}{4} 48−c​)，两个厂商早晚都会增产，只有达到纳什均衡产量( 8 − c 3 \frac {8-c}{3} 38−c​, 8 − c 3 \frac {8-c}{3} 38−c​)后才会稳定下来,因为这时任意一个厂商单独改变产量都不利于自己。如果将遵守还是突破限额作为厂商面临的选择,则构成如下图所示中得益矩阵表示的博弈。不难看出,下图所示是一个囚徒困境。

上述博弈是根据谢识予老师的《经济博弈论》中连续产量古诺模型改编得到的比较简单版本。更复杂的模型可以包括n个寡头,市场出清价格与市场总产量的函数关系P=P(Q) 可以更复杂,每个厂商的成本也可以变化或不同。但不管这些因素如何变化,分析思路与上述模型是相似的,不过纳什均衡的产量组合将变成n个偏微分为0的联立方程组解。

产量博弈的古诺模型是一种囚徒困境,无法实现博弈方总体和各个博弈方各自最大利益的结论，该博弈说明自由竞争经济同样存在低效率问题，放任自流并非最好的政策。这些结论也说明了,政府对市场调控和监管的必要性。