汉诺塔部分核心内容来自《程序员的数学》一书。

图上这个游戏，名叫汉诺塔，不知道大家有没有玩过，传说印度教的创造之神大梵天在创造世界时顺手搞了三根柱子，在一根柱子上从上到下按小到大的顺序摞着一堆圆环，然后命令婆罗门把这些圆片全部移到另一根柱子，但是有一些规则，如下：

1.一次只能转移一个圆环到一根柱子上

2.圆环上面不能放比它小的圆环

戳这个网址试试吧：http://www.hannuota.cn/。三层是不是so easy，四层呢？五层呢？是不是就凌乱了，它的最少移动次数又是怎么计算出来的呢？

假设第一根柱子是起始柱，第二根为目标柱，第三根为中转柱。

让我们从只有一个圆环的情况开始吧。

只有一个圆环，那么只要把它移动到目标柱子就可以了，最少移动次数就是1步。

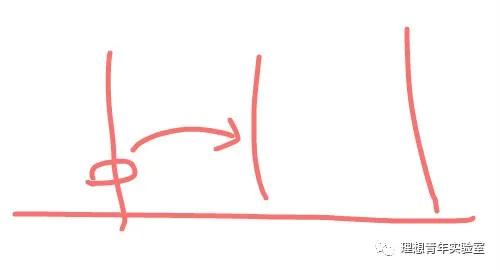
接下来是两个圆环。

因为小的圆环上面不能放大的，所以小圆环不能先移到目标柱上，否则大的放不了，那么就先把它移动到中转柱上，一步就搞定了，接下来把大的移到目标柱上，最后把小的移到目标柱上，最少次数为3次。

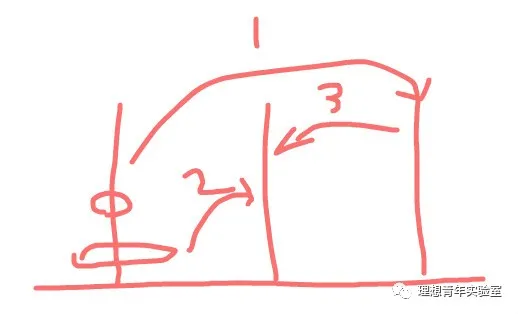
接下来是3个圆环。

移动方式如下图所示，最少次数为7次。

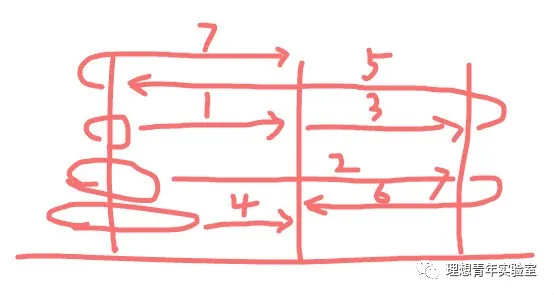
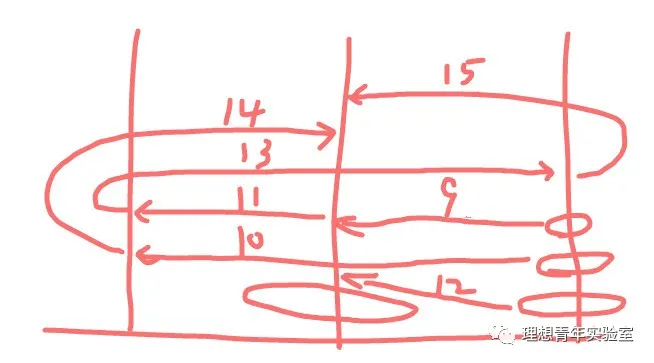
4个圆环的步骤图如下：

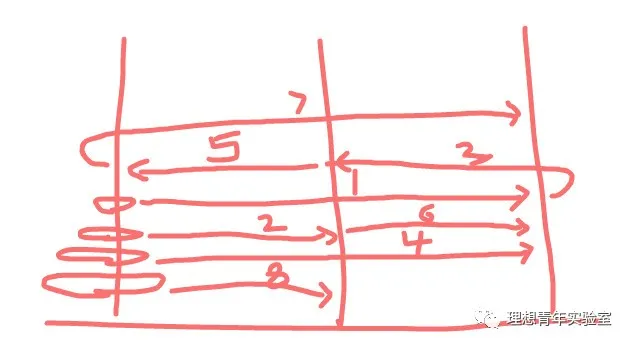
因为步骤较多一个图画不完，所以分两个图画，上面这个图的最后状态是上面三个圆环都移到了最右边柱子上，最大的圆环移到了中间目标柱上，所以接下来的步骤如下，总的移动次数为15：

仔细观察上述几个图，首先会发现最大的圆环都只移动了一次，从起始柱移到目标柱，其次是最大的圆环移动之前，剩余的圆环都完整的移动到了中转柱上，最后是最大的圆环移动之后剩余的圆环也都移到了目标柱上，所以除了最大的圆环剩下的圆环都完整的移动了两次，而如果忽略最大的圆环的话，那么其实会发现整个过程中是做两次n-1层汉诺塔，而解n-1层汉诺塔时如果再忽略最大圆环的话，就是做两次n-2层汉诺塔，这样一直下去，直到做一层汉诺塔，其实这就是个递归结构，那么可以归纳n层汉诺塔的解法如下：

设x为起点柱，y为目标柱，z为中转柱，n层汉诺塔即利用中转柱z将n个圆环从起点柱x转移至目标柱y。

1.n=0时：

没有圆环，不做任何动作；

2.n>0时：

首先，将n-1个圆环从x柱，经由y柱中转，移到z柱（解出n-1层汉诺塔）；

其次，将最大的1个圆环从x柱移到y柱；

最后，将n-1个圆盘从z柱，经由x柱中转，移到y柱（解出n-1层汉诺塔）；

将解出“n层汉诺塔”所需的最少移动次数表示为H(n)，那么有如下等式：

H(n) = 0，n为0的时候 H(n-1) + 1 + H(n-1)，n>0时

上述H(n)和H(n-1)的关系称为递推公式。

所以5层汉诺塔的最少移动次数：

H(5)=H(4) + 1 + H(4)=31 H(4)=H(3) + 1 + H(3)=15 H(3)=H(2) + 1 + H(2)=7 H(2)=H(1) + 1 + H(1)=3 H(1)=H(0) + 1 + H(0)=1 H(0) = 0

从下往上带入计算，即可求出5层汉诺塔的最少移动次数为31。

这里使用JavaScript代码来演示n层汉诺塔的解法和最少移动次数：

有兴趣的可以对着这个步骤来移动汉诺塔，检验是否正确。

上面找规律来解决的方式是我在知道答案后的马后炮行为，只用来帮助更好的理解和解决汉诺塔这个游戏，并不具有通用性。

到这里就要有请另一个主角【递归】登场了，递归，就是自己调用自己。它通常用来把复杂的大问题层层转化为类似的小问题，先解决小问题再返回解决大问题的一种思想。

递归包含递和归两个步骤，要使用递归来解决一个问题首先要先判断该问题是否能分解成有相同思路的子问题，代码层面来说，就是是否能调用同一个函数来解决；其次是是否有边界条件，即分解到某一个子问题后发现不能再分解了，否则一直下去没有尽头，那就不叫递归了，叫永递，即永远的递下去（什么乱七八糟的）。其中递归函数里怎么继续再调用自身通常是需要找到一个大问题和小问题之间的联系的，也就是上面提到的递推公式，这是用递归来解决问题最难的部分，编写代码往往是很简单的。

但是不要怕，万事都有套路，解决递归问题的一般套路如下：

1.先定义一个函数，明确这个函数要干什么，具体的函数内容可以先不写；

2.寻找递归结束的条件，即当函数参数为什么时返回，不再继续调用自身，找到后在函数内写出来；

3.最重要的一步，找到问题和子问题间的联系，即找到递推公式，对于函数来说，也就是函数参数要怎么缩小，在函数内用代码表示出来。

搞定。

理论是简单的，接下来实践一下。

首先来看上一篇里提到的n的阶乘问题：n!=nn-1n-2.....21，很明显是符合递归特征的，比如5!=54!，4!=43!，所以一个大的阶层是可以分解成小的阶层来计算的，用上面的套路来用递归计算它。

1.定义一个函数

2.寻找递归结束条件

通过上面的等式很明显知道n为1时就结束了，而1的阶层我们是知道的，为1。