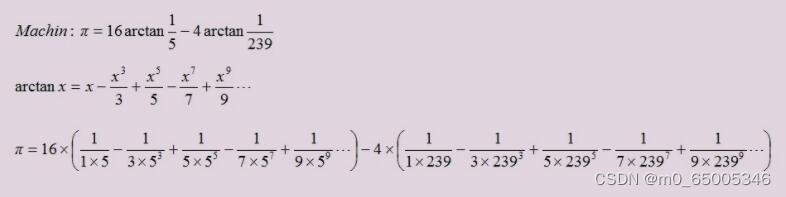【Python】计算任意位数的圆周率π(Machin Formula) |
您所在的位置:网站首页 › 圆周率32565380位 › 【Python】计算任意位数的圆周率π(Machin Formula) |
【Python】计算任意位数的圆周率π(Machin Formula)
|
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 一、马青公式 二、Python代码实现 1.理清思路 2.C++版本 总结 前言今天的python课,我给学生介绍math库。其中一个孩子问,能看到PI的值吗?我马上开始了我的表演。进入命令行,导入,调用math.pi,一气呵成。谁知,这孩子并不买账!嚷嚷道:我要看小数点后100位@@@ 一、马青公式Machin公式:π=16arctan(1/5)-4arctan(1/239)
计算π 的公式已经拿到,我们有一个明确的想要精确的π的位数,那么当式子中n越大的时候,第n项就会越小,小到计算这个精确目标时可以忽略的地步。 注意1:由于程序中浮点数的有效位数有限(小数点后很长的话会被省略,很大的数如果是小数也会用科学技术法),会损失很大精度,所以用整数来计算π。 比如想计算小数点后 7 位,就计算 π * 10^7 是多少,返回 31415926。 比如想计算小数点后 3 位,程序就会给你返回整数 3141,是扩大了 10^3 的结果。注意2: 想用整数计算 π,那除法的时候就要使用取模运算来保证结果也是整数,以达到保证精度的目的。 注意3: 用取模操作代替除法,但是取模对于除法来说本身就是有精度损失的,为了弥补这部分精度,可以先把想精确的位数增加 k,最后把结果减少 k 位。 注意4: 注意n:求 π 的数学公式中的 n,还是精确 到π 的位数。 代码如下(python): # 计算准确圆周率的马青公式 import time n = int(input('请输入圆周率小数点后的位数:')) start_time = time.time() # 计算pi计时起点 w = n + 10 # 考虑精度,位数增加 k,结果减少 k 位 b = 10 ** w # 用整数计算pi 如3.14 * 10^2 = 314 x1 = b * 4// 5 # 第一项前半部分 x2 = b // -239 # 第一项后半部分 sum = x1 + x2 # 第一项的值 n *= 2 for i in range(3, n, 2): x1 //= -25 x2 //= -239*239 x = (x1+x2)//i sum += x mpi = sum * 4 mpi //= 10**10 end_time = time.time() run_time = str(end_time - start_time) mpi_str = str(mpi) mpi_str = mpi_str[:1] + '.' + mpi_str[1:] # f = open('mpi.txt', 'w') # f.write(mpi_str) # f.close() print('运行时间: ' + run_time) print('计算结果: ',mpi_str) print('') 2.C++版本代码如下(C++): /********************************************************** *使用梅钦公式π=16arctan(1/5)-4arctan(1/239) *通过建立数组来储存超过类型范围的小数部分 *用long类型数组pi[ ]来储存各项(每一项有4位) *使用long类型term[ ]来实现对每一次泰勒展开结果的储存 *之后通过进位等操作,实现用数组储存足够位数的π。 ***********************************************************/ void machin_pi(long L) { //常量C用于进位退位操作,10000代表pi数组以四位进行储存 const long C = 10000; //flag用于正负号的判定 short flag; //梅钦公式具体应用时π=80*(1/25-1/(25*25*3)+......)+(-956)*(......) //xishu[]为两项展开的外系数,div[]为每次进阶指数所用的除数 //odd为1,3,5等奇数,shang_1,r_1是进阶指数的商和余数,r_2是计算π各项的余数 long xishu[2] = { 80,-956 }, div[2] = { 25,57121 },odd,shang_1, r_1, r_2,i=0,j,t,tt,k=0,len=L; L = L / 4 + 3; //term[]用来完成对每个升幂项的足够长度保存 //pi[]用来储存最后结果 long *term = new long[L]; long *pi = new long[L]; while (i < L)pi[i++] = 0; while (k - 2) { //完成对term的初始化 flag = 1; term[0] = xishu[k]; i = 1; while (i < L) { term[i] = 0; ++i; } for (i = 0,odd=1; i < L; ++i) { j = i; for (r_1=r_2 = 0;j < L; ++j) { t = r_1 * C + term[j]; //t、r_1、term[]用来储存25与57121的各幂 term[j] = t / div[k]; //每次进阶都用上一轮已经算好的term数组进行升阶(后一项都是前一项除以25或57121) r_1 = t % div[k]; //保存余数,在下一项中×C用于退位 tt = r_2 * C + term[j]; //tt、r_2、shang_1用来储存泰勒展开各项 shang_1 = tt / odd; //在term[]的基础上除以奇数1、3、5等 r_2 = tt % odd; //保存余数,在下一项中用于退位 pi[j] += (flag?shang_1:-shang_1); //用flag进行标定正负号 } if (term[i])--i; //当term[i]==0时,后续展开不会影响这一项(这四位小数),进行++i,直接从下一项开始 odd += 2; flag=!flag; //泰勒展开正负号改变 } ++k; //处理完arccot5后进入下一轮处理arccot239 } k = 0; //上述循环之后,pi[]中已经储存了各项数据 //但pi[]中数据可能存在负数、五位数及以上等等情况 //接下来的循环进行处理,通过进位全部转化成正四位数 while (--i) { pi[i] += k; if (pi[i] < 0) { k = pi[i] / C-1; pi[i] %= C; pi[i] += C; } else { k = pi[i] / C; pi[i] %= C; } } //输出圆周率 printf("3."); for (i = 1; i < len / 4 + 1; ++i) { printf("%04ld", pi[i]); } switch (len%4) { case 0:break; case 1:printf("%01ld", pi[i]/ 1000); break; case 2:printf("%02ld", pi[i]/ 100); break; case 3:printf("%03ld", pi[i]/ 10); break; } //释放内存 delete[] term; delete[] pi; } 总结注意3中提出的这个方案是有漏洞的,因为 k 是被固定在程序中的,随着用户输入 n 的增大,越来越大量的取模运算损失的精度,必定是固定不变的 k 值所不能弥补的。所以对每一个固定的 k,一定会有一个 n 值,使得本程序所计算的结果是错误的。 对此,我还有一个方案,k 值不固定,由 n 计算得出,n 越大就取越大的 k。但我不想随便定一个 k 与 n 的关系,当然通过代码可以试出一个不错的,但程序计算总有尽头,没有理论支持就无法证明这个关系是真正合理的。当 k 取 10 时,n 取 100000 还都没有出现误差。 |
【本文地址】
今日新闻 |
推荐新闻 |