挑战408 |
您所在的位置:网站首页 › 图的算法会考吗 › 挑战408 |
挑战408
|
图由顶点及其边组成,图的遍历主要分为两种: 遍历所有顶点遍历所有边 图的遍历我们只讨论第一种情况,即不重复的列出所有的顶点,主要有两种策略:深度优先搜索(DFS),广度优先搜索(BFS) 为了使深度和广度优先搜索的实现算法的机制更容易理解,假设提供了一个名为visit的函数,它负责处理每个单独节点所需的任何处理。 因此,遍历的目的是按照确定的连接顺序在每个节点上调用且仅调用一次该函数。 因为图形通常具有前往相同节点的许多不同路径,所以确保遍历算法不会多次访问同一节点我们需要额外的变量来跟踪已经访问过哪些节点。 为此,接下来的两个部分中的实现定义了一组名为visited的节点,以跟踪已经处理的节点。 visit() //对节点进行相应的操作visited //标记已访问过的节点,可以用vector或者set,栈存储都可以,这里我们使用set来存储foreach(A in B) 在A中搜索符合条件B的元素(遍历) 深度优先搜索(Depth-first search)遍历图的深度优先策略类似于树的前序遍历,并具有相同的递归结构。 唯一的复杂因素是图表可以包含环。 因此,必须跟踪已经访问过的节点。 下面的代码实现的是从某个特定的节点出发进行的深度优先搜索。 /* *数据结构 node *说明:节点的数据结构、 /* struct Node { string name; //节点名称 set arcs; //该节点的边的集合 }; /* *结构:Arc *说明:边的数据结构 */ struct Arc { Node *start; //即从哪个节点出发 Node *finish; //即指向哪个节点 double cost;//边的权重 }; * 函数 :depthFirstSearch * 用法: depthFirstSearch(node); * ------------------------------ * 用指定的节点来初始化DFS的起始节点 */ void depthFirstSearch(Node *node) { Set visited; visitUsingDFS(node, visited); } /* * 函数: visitUsingDFS * 用法: visitUsingDFS(node, visited); * ------------------------------------ * 从特定的节点执行DFS ,并避免重复遍历相关节点 */ void visitUsingDFS(Node *node, set & visited) { //如果在visited集合中存在该节点,说明为simple case,直接返回 if (visited.contains(node)) return; //否则 visit(node);//对该节点进行相应操作 visited.add(node);//将该节点添加到visited集合中 foreach (Arc *arc in node->arcs) { //对每一个节点递归调用DFS算法 visitUsingDFS(arc->finish, visited); } } DFS的具体过程下面用一个实例来体会一下DFS的具体过程。还是上次的那张图: 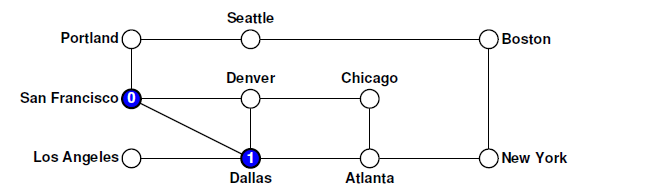 根据我们的代码,我们必须在San Francisco寻找其他路径时,完成对Dallas节点的DFS调用。因此根据我们假设的优先访问规则,下一个要访问的节点就是Atlanta: 根据我们的代码,我们必须在San Francisco寻找其他路径时,完成对Dallas节点的DFS调用。因此根据我们假设的优先访问规则,下一个要访问的节点就是Atlanta:  因此对于Atlanta节点而言,有两个节点相邻,我们根据字母表的优先,选择Chicago节点和Denver节点。(因为此时的Dallas已经被标记,不在作为节点选择参考的对象)。以此类推: 因此对于Atlanta节点而言,有两个节点相邻,我们根据字母表的优先,选择Chicago节点和Denver节点。(因为此时的Dallas已经被标记,不在作为节点选择参考的对象)。以此类推: 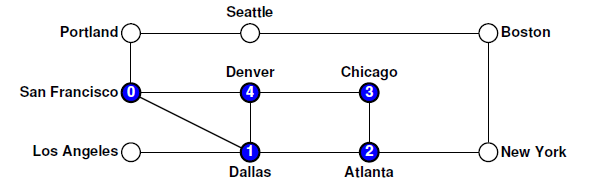 然而,当程序走到Denver节点时,发现已经没有可以走的路了,因为周围的节点都被标记过,那么只能往后回溯(就是后退),后退的第一个节点是Chicago,显然情况跟Denver节点一样,那么继续回溯,是Atlanta节点,发现该节点还有一条未被探索的路径,所以它回溯到Atlanta节点后,选择了New York节点,继续执行DFS: 然而,当程序走到Denver节点时,发现已经没有可以走的路了,因为周围的节点都被标记过,那么只能往后回溯(就是后退),后退的第一个节点是Chicago,显然情况跟Denver节点一样,那么继续回溯,是Atlanta节点,发现该节点还有一条未被探索的路径,所以它回溯到Atlanta节点后,选择了New York节点,继续执行DFS: 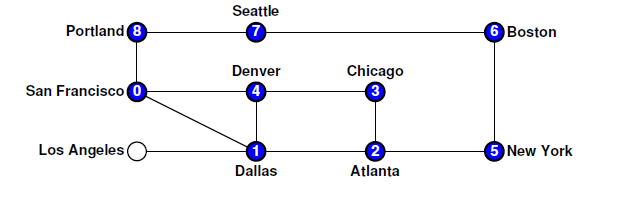 同样,以此类推,程序执行到Portland,开始回溯,一直到Dallas。(路径显然为8 -> 7 -> 6 -> 5 ->2).发现Dallas还有未被探索的路径。于是找到LosAngeles节点,继续执行DFS。至此,图中所有的节点都遍历完毕: 同样,以此类推,程序执行到Portland,开始回溯,一直到Dallas。(路径显然为8 -> 7 -> 6 -> 5 ->2).发现Dallas还有未被探索的路径。于是找到LosAngeles节点,继续执行DFS。至此,图中所有的节点都遍历完毕: 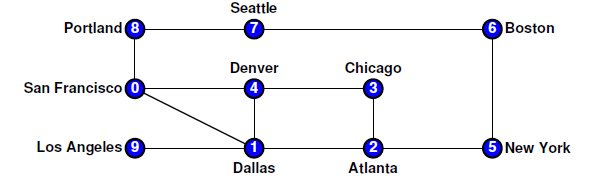
当然我们可以更为方便的用栈来存放标记的元素,这样我们可以在回溯的时候,将元素从栈中弹出即可。当栈空时即表明图的遍历完成,栈始终不空,表明图中有一直不能访问到的点,因为没有路径通过,此时图为不连通的。(这就是典型的回溯算法!) 实例分析(1)那么同样的对于下面的有向图,也可以如下进行搜索,如图 如果我们用true或者false来表示节点是否被访问,那么假设从H出发访问C节点,初始状态应该是这样的: DFS的栈实现,也可以采用非递归算法实现。 dfs from v1 to v2: create a stack, s //创建一个空的栈s s.push(v1) //将起始节点入栈 while s is not empty://当栈不为空时 v = s.pop() //将栈中的元素弹出,并赋值给节点类型的变量V if v has not been visited://如果v没有被访问 mark v as visited//标记V //将所有v节点的邻居入栈 push all neighbors of v onto the stack我们就用上面的步骤继续分析一下DFS的具体数据在栈中的情况(从H到C)。 一开始我们建立一个空的栈,将节点h入栈,此时栈中只有元素H: 此时的栈不为空了, 在while循环中执行赋值语句后,v = h,此时h节点尚未被标记,于是标记点h,并且将h的所有邻居节点入栈,(为什么G节点不是?因为这是有向图); 此时的栈不为空了, 在while循环中执行赋值语句后,v = h,此时h节点尚未被标记,于是标记点h,并且将h的所有邻居节点入栈,(为什么G节点不是?因为这是有向图);  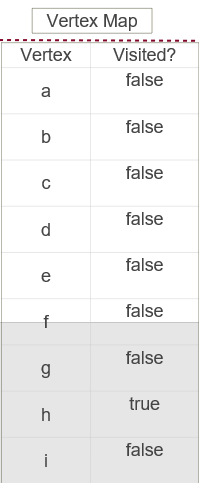 同样这里因为F是栈顶,所以我们先弹出的是节点F,同样执行上述操作,F的邻居是C,所以把C入栈,即如图所示: 同样这里因为F是栈顶,所以我们先弹出的是节点F,同样执行上述操作,F的邻居是C,所以把C入栈,即如图所示: 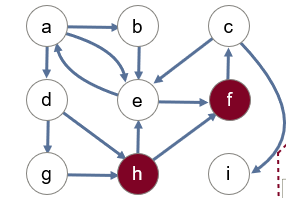  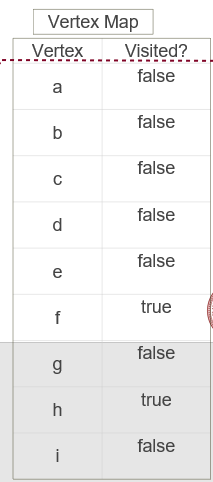 ,同样执行上述操作,F的邻居是C,所以把C入栈,即如图所示: ,同样执行上述操作,F的邻居是C,所以把C入栈,即如图所示:  在下一次循环中 我们发现 在下一次循环中 我们发现 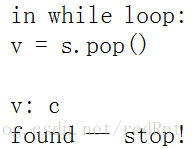 栈中弹出的值恰好就是我们要寻找的值,于是停止搜索。也就是说这样的效率比递归要高: 栈中弹出的值恰好就是我们要寻找的值,于是停止搜索。也就是说这样的效率比递归要高: 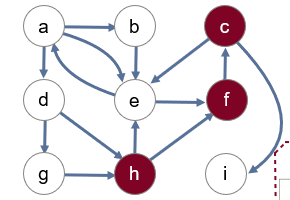 DFS的递归和迭代解决方案都是正确的,但由于递归与使用堆栈的细微差别,它们以不同的顺序遍历节点。 DFS的递归和迭代解决方案都是正确的,但由于递归与使用堆栈的细微差别,它们以不同的顺序遍历节点。
对于h到c的例子,迭代解决方案碰巧更快,但对于不同的图,递归解决方案通常可能更快解决。 总结:在给定节点处调用DFS可以查找从该节点开始所有可到达的节点。(由此判断图是否为连通的) 如果我们有一个邻接列表,在n个节点,m条边的图中执行DFS,需要时间O(m + n),空间O(n)。 |
【本文地址】
今日新闻 |
推荐新闻 |
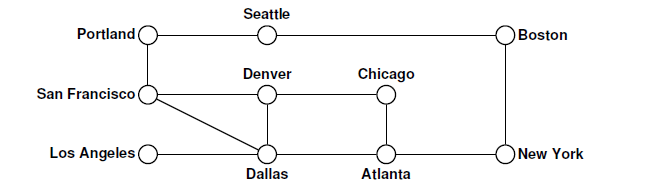 节点被绘制为空心圆圈以指示它们尚未被访问。 随着算法的进行,这些圆圈中的每一个都将标有记录处理该节点的顺序的数字。 对depthFirstSearch函数本身的调用会创建一个空的set集合,然后将控制权移交给递归的visitUsingDFS函数。 假设我们的算法从节点San Francisco处开始,该节点记录在图中,如下所示:
节点被绘制为空心圆圈以指示它们尚未被访问。 随着算法的进行,这些圆圈中的每一个都将标有记录处理该节点的顺序的数字。 对depthFirstSearch函数本身的调用会创建一个空的set集合,然后将控制权移交给递归的visitUsingDFS函数。 假设我们的算法从节点San Francisco处开始,该节点记录在图中,如下所示: 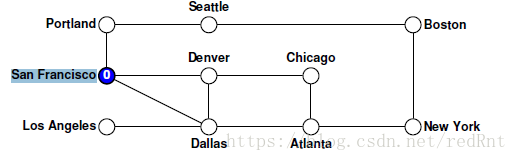 下面我们就具体的代码来分析整个过程:
下面我们就具体的代码来分析整个过程: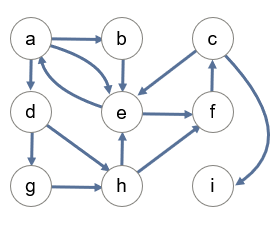 假设从节点A开始用DFS算法进行遍历,我们使用栈来存储标记过的节点。 我们知道,在DFS中,我们采用的是递归的方式进行实现的,并且给每一个遍历过的点都做上了标记,目的是为了防止程序进入死循环。(为什么树可以不需要呢?因为树没有环) 利用之前专栏提到的递归模式,我们可以写出下面的伪代码:
假设从节点A开始用DFS算法进行遍历,我们使用栈来存储标记过的节点。 我们知道,在DFS中,我们采用的是递归的方式进行实现的,并且给每一个遍历过的点都做上了标记,目的是为了防止程序进入死循环。(为什么树可以不需要呢?因为树没有环) 利用之前专栏提到的递归模式,我们可以写出下面的伪代码: 而调用栈此时应该是这样的:
而调用栈此时应该是这样的:  根据按字母表顺序优先访问的规则此时,访问的下一个节点应该是节点E,此时对应的内容为:
根据按字母表顺序优先访问的规则此时,访问的下一个节点应该是节点E,此时对应的内容为: 
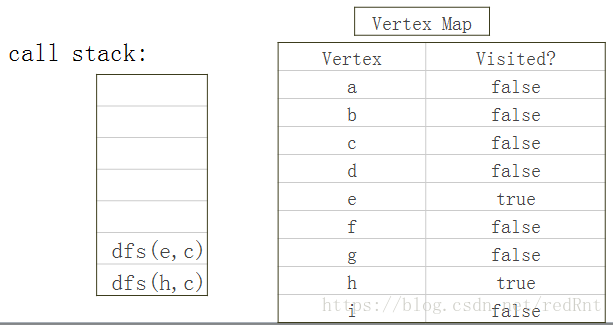 如此继续,直到调用到顶点G的时候,已经没有未标记的路可以走了,此时开始回溯:
如此继续,直到调用到顶点G的时候,已经没有未标记的路可以走了,此时开始回溯: 
 回溯的过程就是将函数调用出栈的过程:
回溯的过程就是将函数调用出栈的过程:  回到节点E,继续调用dfs算法:
回到节点E,继续调用dfs算法:  此时找到H->C的路径。
此时找到H->C的路径。