图像增强 |
您所在的位置:网站首页 › 图片锐化是什么样子的 › 图像增强 |
图像增强
|
文章目录
1. 图像锐化1.1. 图像细节的灰度变化特性
2. 锐化处理方法2.1. 微分法2.1.1. 梯度法2.1.1.1. 直接以梯度代替锐化输出2.1.1.2. 输出阈值判断2.1.1.3. 为边缘规定一个特定的灰度级2.1.1.4. 为背景规定特定的灰度级2.1.1.5. 二值化图像
2.2. 罗伯特梯度算子法2.3. 拉普拉斯算子法2.4. 高通滤波法2.5. 模板匹配法2.5.1. Sobel算子2.5.2. Prewitt算子
3. 一些边缘检测的经验
1. 图像锐化
图像锐化与图像平滑是相反的操作,锐化是通过增强高频分量来减少图像中的模糊,增强图像细节边缘和轮廓,增强灰度反差,便于后期对目标的识别和处理。锐化处理在增强图像边缘的同时也增加了图像的噪声。方法通常有微分法和高通滤波法。 1.1. 图像细节的灰度变化特性取图像中的某一行作为扫描行,其灰度变化曲线为: 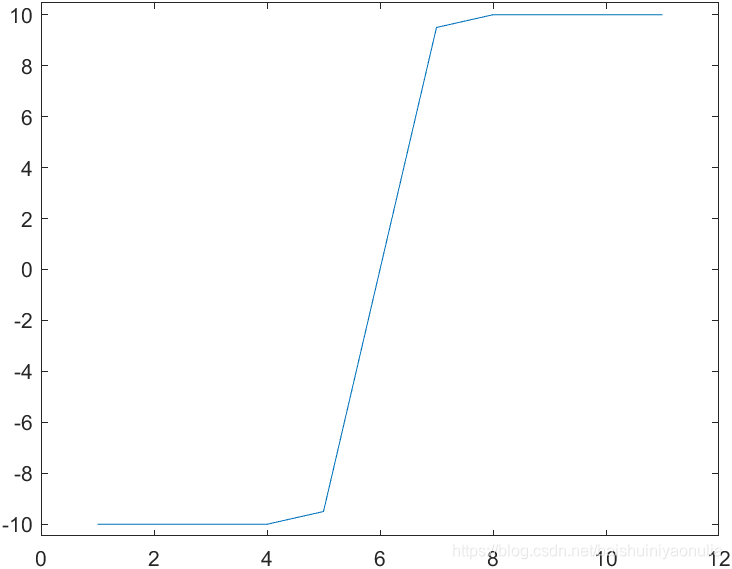  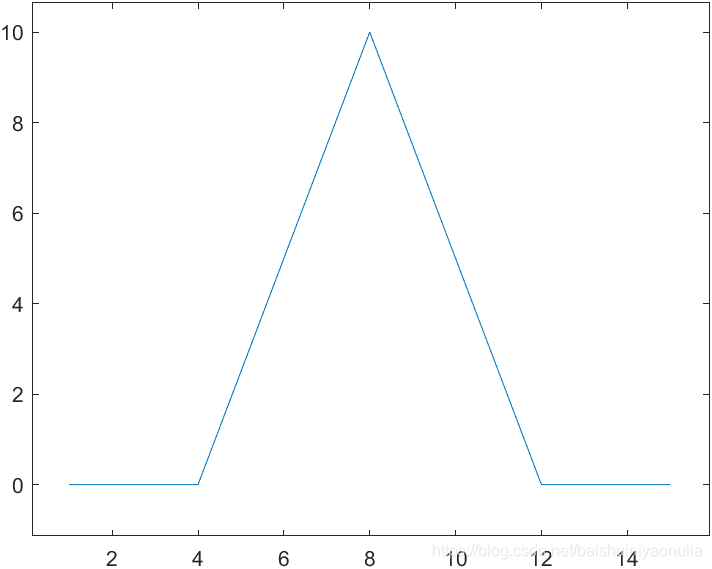 一阶微分 一阶微分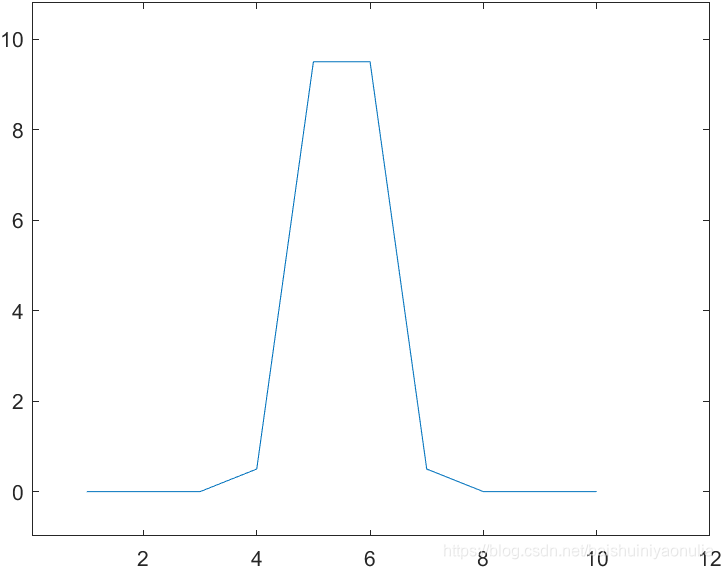 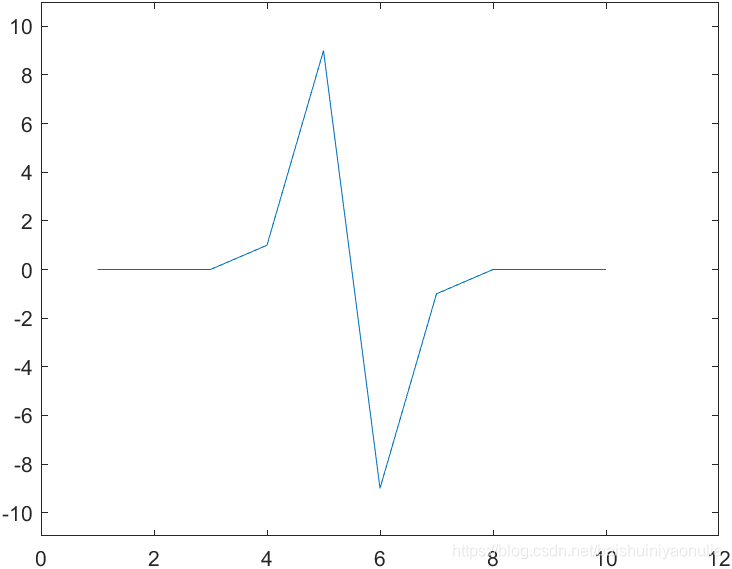 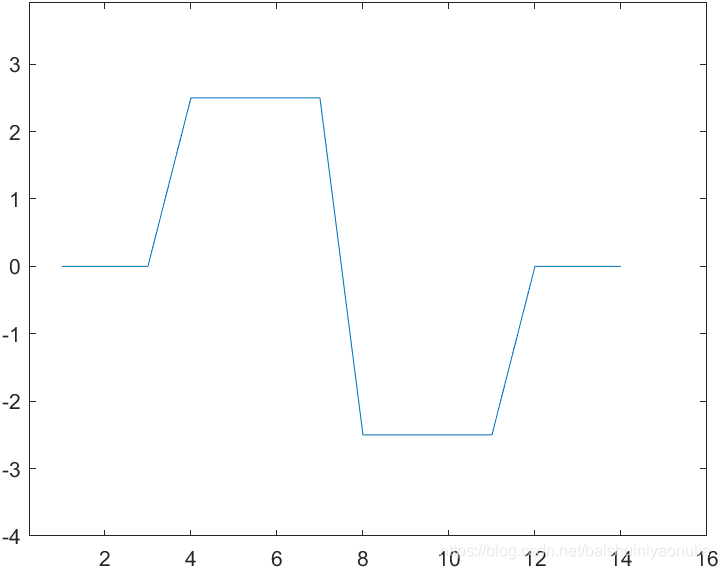 二阶微分 二阶微分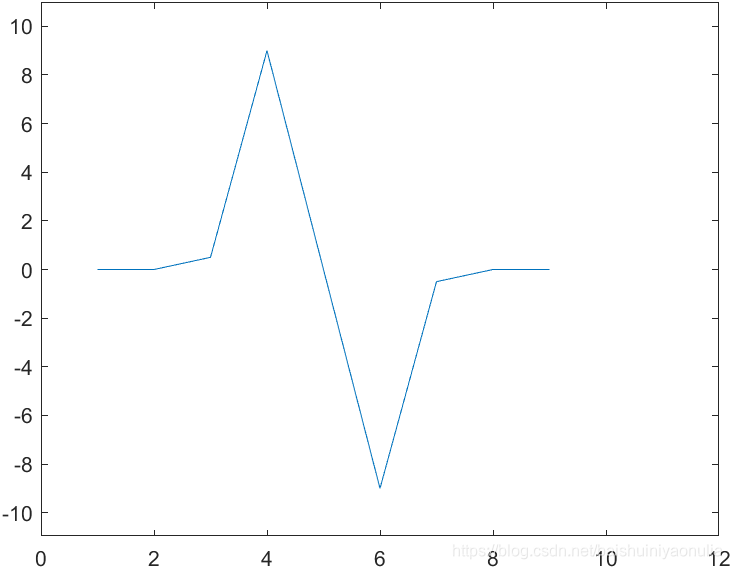 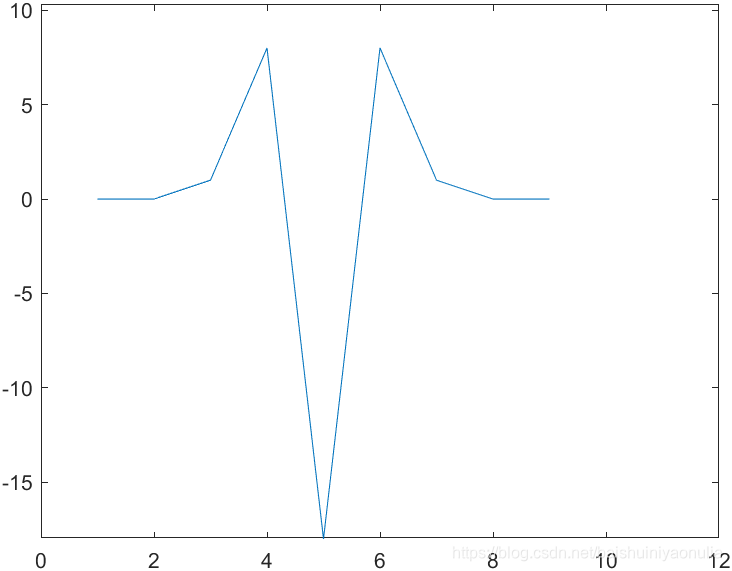 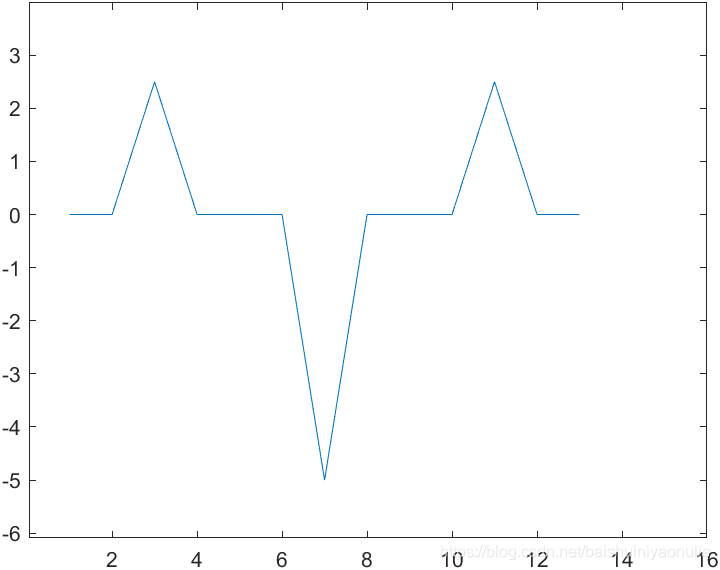 2. 锐化处理方法
2.1. 微分法
2.1.1. 梯度法
2. 锐化处理方法
2.1. 微分法
2.1.1. 梯度法
梯度的方向是图像中最大变化率的方向,梯度的幅度比例于相邻像素的灰度级差值 对图像 F ( x , y ) F(x,y) F(x,y),在点 ( x , y ) (x,y) (x,y)处的梯度定义为矢量: ∇ F ( x , y ) = [ ∂ F ∂ x ∂ F ∂ y ] \nabla F(x,y)=\begin{bmatrix} \frac{\partial F}{\partial x} \\ \\ \frac{\partial F}{\partial y} \\ \end{bmatrix} ∇F(x,y)=⎣⎡∂x∂F∂y∂F⎦⎤其幅度(模)为: ∣ ∇ F ( x , y ) ∣ = ( ∂ F ∂ x ) 2 + ( ∂ F ∂ y ) 2 |\ \nabla F(x,y)\ |=\sqrt{( \frac{\partial F}{\partial x})^2+( \frac{\partial F}{\partial y})^2} ∣ ∇F(x,y) ∣=(∂x∂F)2+(∂y∂F)2 在进行图像处理时所称的梯度通常是指梯度的模。 对于离散图像,一般用邻近相差的差分法来代替微分: G ( x , y ) = ∇ F ( x , y ) G(x,y)=\nabla F(x,y) G(x,y)=∇F(x,y)该方法简单,但是在图像均匀的区域由于梯度很小,会导致锐化输出图像整体偏暗 2.1.1.2. 输出阈值判断G ( x , y ) = { ∇ F ( x , y ) , ∇ F ( x , y ) > T F ( x , y ) , o t h e r w i s e G(x,y) = \begin{cases} \nabla F(x,y), & \nabla F(x,y)>T \\ F(x,y), & otherwise \end{cases} G(x,y)={∇F(x,y),F(x,y),∇F(x,y)>Totherwise该方法不会破坏图像背景,同时又可以进行一定程度的图像锐化 2.1.1.3. 为边缘规定一个特定的灰度级G ( x , y ) = { L α , ∇ F ( x , y ) > T F ( x , y ) , o t h e r w i s e G(x,y) = \begin{cases} L_\alpha, & \nabla F(x,y)>T \\ F(x,y), & otherwise \end{cases} G(x,y)={Lα,F(x,y),∇F(x,y)>Totherwise 2.1.1.4. 为背景规定特定的灰度级G ( x , y ) = { ∇ F ( x , y ) , ∇ F ( x , y ) > T L β , o t h e r w i s e G(x,y) = \begin{cases} \nabla F(x,y), & \nabla F(x,y)>T \\ L_\beta, & otherwise \end{cases} G(x,y)={∇F(x,y),Lβ,∇F(x,y)>Totherwise 2.1.1.5. 二值化图像G ( x , y ) = { L α , ∇ F ( x , y ) > T L β , o t h e r w i s e G(x,y) = \begin{cases} L_\alpha, & \nabla F(x,y)>T \\ L_\beta, & otherwise \end{cases} G(x,y)={Lα,Lβ,∇F(x,y)>Totherwise 2.2. 罗伯特梯度算子法Roberts梯度算子法算法简单,无方向性,采用对角相差的差分法来代替微分: Laplacian算法是线性二次微分算子,与梯度算子一样具有旋转不变性,从而满足了不同方向的图像边缘锐化要求,其获得的边界比较细,包括较多的细节信息,但边界不清晰 Laplacian算子: ∇ 2 F ( x , y ) = ∂ 2 F ( x , y ) ∂ x 2 + ∂ 2 F ( x , y ) ∂ y 2 \nabla^2 F(x,y)=\frac{\partial^2 F(x,y)}{\partial x^2}+\frac{\partial^2 F(x,y)}{\partial y^2} ∇2F(x,y)=∂x2∂2F(x,y)+∂y2∂2F(x,y)其离散形式为: ∇ 2 F ( x , y ) = { [ F ( x + 1 , y ) − F ( x , y ) ] − [ F ( x , y ) − F ( x − 1 , y ) ] } + { [ F ( x , y + 1 ) − F ( x , y ) ] − [ F ( x , y ) − F ( x , y − 1 ) ] } = F ( x + 1 , y ) + F ( x − 1 , y ) + F ( x , y + 1 ) + F ( x , y − 1 ) − 4 F ( x , y ) \begin{aligned} \nabla^2 F(x,y) & = \{\ [F(x+1,y)-F(x,y)]-[F(x,y)-F(x-1,y)]\ \}+\{\ [F(x,y+1)-F(x,y)]-[F(x,y)-F(x,y-1)]\ \} \\ & = F(x+1,y)+F(x-1,y)+F(x,y+1)+F(x,y-1)-4F(x,y) \\ \end{aligned} ∇2F(x,y)={ [F(x+1,y)−F(x,y)]−[F(x,y)−F(x−1,y)] }+{ [F(x,y+1)−F(x,y)]−[F(x,y)−F(x,y−1)] }=F(x+1,y)+F(x−1,y)+F(x,y+1)+F(x,y−1)−4F(x,y)可以看出,Laplacian算子就是其4倍中心元素值与其领域值和之差的绝对值,也可表达为中心元素与其领域内元素和均值负5倍的绝对值: ∇ 2 F ( x , y ) = ∣ − 5 { F ( x , y ) − 1 5 [ F ( x − 1 , y ) + F ( x , y − 1 ) + F ( x , y ) + F ( x , y + 1 ) + F ( x + 1 , y + 1 ) ] } ∣ \nabla^2 F(x,y)=|-5\{\ F(x,y)-\frac{1}{5}[F(x-1, y)+F(x, y-1)+F(x,y)+F(x,y+1)+F(x+1,y+1)]\ \}| ∇2F(x,y)=∣−5{ F(x,y)−51[F(x−1,y)+F(x,y−1)+F(x,y)+F(x,y+1)+F(x+1,y+1)] }∣ 使用Laplacian算子进行锐化时,其锐化输出 G ( x , y ) G(x,y) G(x,y)为: G ( x , y ) = F ( x , y ) − ∇ 2 F ( x , y ) G(x,y)=F(x,y)-\nabla^2F(x,y) G(x,y)=F(x,y)−∇2F(x,y) 常用的三种Laplacian算子: [ 0 − 1 0 − 1 4 − 1 0 − 1 0 ] [ − 1 − 1 − 1 − 1 8 − 1 − 1 − 1 − 1 ] [ 1 − 2 1 − 2 4 − 2 1 − 2 1 ] \begin{bmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \\ \end{bmatrix}\ \ \ \ \ \ \begin{bmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \\ \end{bmatrix}\ \ \ \ \ \ \begin{bmatrix} 1 & -2 & 1 \\ -2 & 4 & -2 \\ 1 & -2 & 1 \\ \end{bmatrix} ⎣⎡0−10−14−10−10⎦⎤ ⎣⎡−1−1−1−18−1−1−1−1⎦⎤ ⎣⎡1−21−24−21−21⎦⎤ 在图像处理中,为了改善锐化的效果,也可以脱离微分计算原理,在原有算子的基础之上对模板系数进行改变,得到Laplacian变形算子 2.4. 高通滤波法图像的边缘与频域中的高频分量相对应,高通滤波器可以抑制低频分量,从而达到图像锐化的目的 建立在离散卷积基础上的空域高通滤波关系式为: g ( μ , ν ) = ∑ x ∑ y F ( x , y ) H ( μ − x + 1 , ν − y + 1 ) g(\mu,\nu)=\sum_{x}^{}\sum_{y}^{}F(x,y)H(\mu-x+1,\nu-y+1) g(μ,ν)=x∑y∑F(x,y)H(μ−x+1,ν−y+1)其中 H ( μ − x + 1 , ν − y + 1 ) H(\mu-x+1,\nu-y+1) H(μ−x+1,ν−y+1)被称作冲激响应 常用的五种归一化冲激响应阵列: H 1 = [ 0 − 1 0 − 1 5 − 1 0 − 1 0 ] H 2 = [ − 1 − 1 − 1 − 1 9 − 1 − 1 − 1 − 1 ] H 3 = [ 1 − 2 1 − 2 5 − 2 1 − 2 1 ] H_1=\begin{bmatrix} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0 & -1 & 0 \\ \end{bmatrix}\ \ \ \ \ \ H_2=\begin{bmatrix} -1 & -1 & -1 \\ -1 & 9 & -1 \\ -1 & -1 & -1 \\ \end{bmatrix}\ \ \ \ \ \ H_3=\begin{bmatrix} 1 & -2 & 1 \\ -2 & 5 & -2 \\ 1 & -2 & 1 \\ \end{bmatrix} H1=⎣⎡0−10−15−10−10⎦⎤ H2=⎣⎡−1−1−1−19−1−1−1−1⎦⎤ H3=⎣⎡1−21−25−21−21⎦⎤ H 4 = 1 7 [ 0 − 2 0 − 2 19 − 2 0 − 2 0 ] H 5 = 1 2 [ − 2 − 1 − 2 − 1 6 − 1 − 2 − 1 − 2 ] H_4=\frac{1}{7}\begin{bmatrix} 0 & -2 & 0 \\ -2 & 19 & -2 \\ 0 & -2 & 0 \\ \end{bmatrix}\ \ \ \ \ \ H_5=\frac{1}{2}\begin{bmatrix} -2 & -1 & -2 \\ -1 & 6 & -1 \\ -2 & -1 & -2 \\ \end{bmatrix} H4=71⎣⎡0−20−219−20−20⎦⎤ H5=21⎣⎡−2−1−2−16−1−2−1−2⎦⎤ 2.5. 模板匹配法将具有8个方向、大小为3×3的模板顺序作用于同一图像窗口,并对结果进行排序,将最大的结果值会加权平均值作为窗口中心元素的锐化进行输出。 模板匹配法除了能增强图像边缘外还具有平滑噪声的优点,总体上效果优于梯度法 下面介绍两种模板匹配算子: 2.5.1. Sobel算子
Prewitt算子有一定的抗干扰性,图像效果比较干净。其有8个方向,分别对应8个模板: ↑ : [ 1 1 1 1 − 2 1 − 1 − 1 − 1 ] ↗ : [ 1 1 1 − 1 − 2 1 − 1 − 1 1 ] → : [ − 1 1 1 − 1 − 2 1 − 1 1 1 ] ↘ : [ − 1 − 1 1 − 1 − 2 1 1 1 1 ] \uparrow:\begin{bmatrix} 1 & 1 & 1 \\ 1 & -2 & 1 \\ -1 & -1 & -1 \\ \end{bmatrix}\ \ \ \ \ \ \nearrow:\begin{bmatrix} 1 & 1 & 1 \\ -1 & -2 & 1 \\ -1 & -1 & 1 \\ \end{bmatrix}\ \ \ \ \ \ \rightarrow:\begin{bmatrix} -1 & 1 & 1 \\ -1 & -2 & 1 \\ -1 & 1 & 1 \\ \end{bmatrix}\ \ \ \ \ \ \searrow:\begin{bmatrix} -1 & -1 & 1 \\ -1 & -2 & 1 \\ 1 & 1 & 1 \\ \end{bmatrix} ↑:⎣⎡11−11−2−111−1⎦⎤ ↗:⎣⎡1−1−11−2−1111⎦⎤ →:⎣⎡−1−1−11−21111⎦⎤ ↘:⎣⎡−1−11−1−21111⎦⎤ ↓ : [ − 1 − 1 − 1 1 − 2 1 1 1 1 ] ↙ : [ 1 − 1 − 1 1 − 2 − 1 1 1 1 ] ← : [ 1 1 − 1 1 − 2 − 1 1 1 − 1 ] ↖ : [ 1 1 1 1 − 2 − 1 1 − 1 − 1 ] \downarrow:\begin{bmatrix} -1 & -1 & -1 \\ 1 & -2 & 1 \\ 1 & 1 & 1 \\ \end{bmatrix}\ \ \ \ \ \ \swarrow:\begin{bmatrix} 1 & -1 & -1 \\ 1 & -2 & -1 \\ 1 & 1 & 1 \\ \end{bmatrix}\ \ \ \ \ \ \leftarrow:\begin{bmatrix} 1 & 1 & -1 \\ 1 & -2 & -1 \\ 1 & 1 & -1 \\ \end{bmatrix}\ \ \ \ \ \ \nwarrow:\begin{bmatrix} 1 & 1 & 1 \\ 1 & -2 & -1 \\ 1 & -1 & -1 \\ \end{bmatrix} ↓:⎣⎡−111−1−21−111⎦⎤ ↙:⎣⎡111−1−21−1−11⎦⎤ ←:⎣⎡1111−21−1−1−1⎦⎤ ↖:⎣⎡1111−2−11−1−1⎦⎤ 3. 一些边缘检测的经验 突变型细节,通过一阶微分的极大值点,二阶微分的零点可以检测出来细线型细节,通过一阶微分的零点,二阶微分的极小值点可以检测出来渐变型细节,一般情况下突变幅度小、定位难,不易检测,但二阶微分的信息比一阶微分多,需进行综合考虑边缘信息具有方向性,不同的锐化/边缘检测算子也可能具有方向性,因此同一个算子对不同的图像检测的效果可能不同,应对不同图像使用不同的算子进行检测 |
【本文地址】
今日新闻 |
推荐新闻 |
 对该灰度变化曲线进行微分,得到一阶微分曲线和二阶微分曲线:
对该灰度变化曲线进行微分,得到一阶微分曲线和二阶微分曲线: 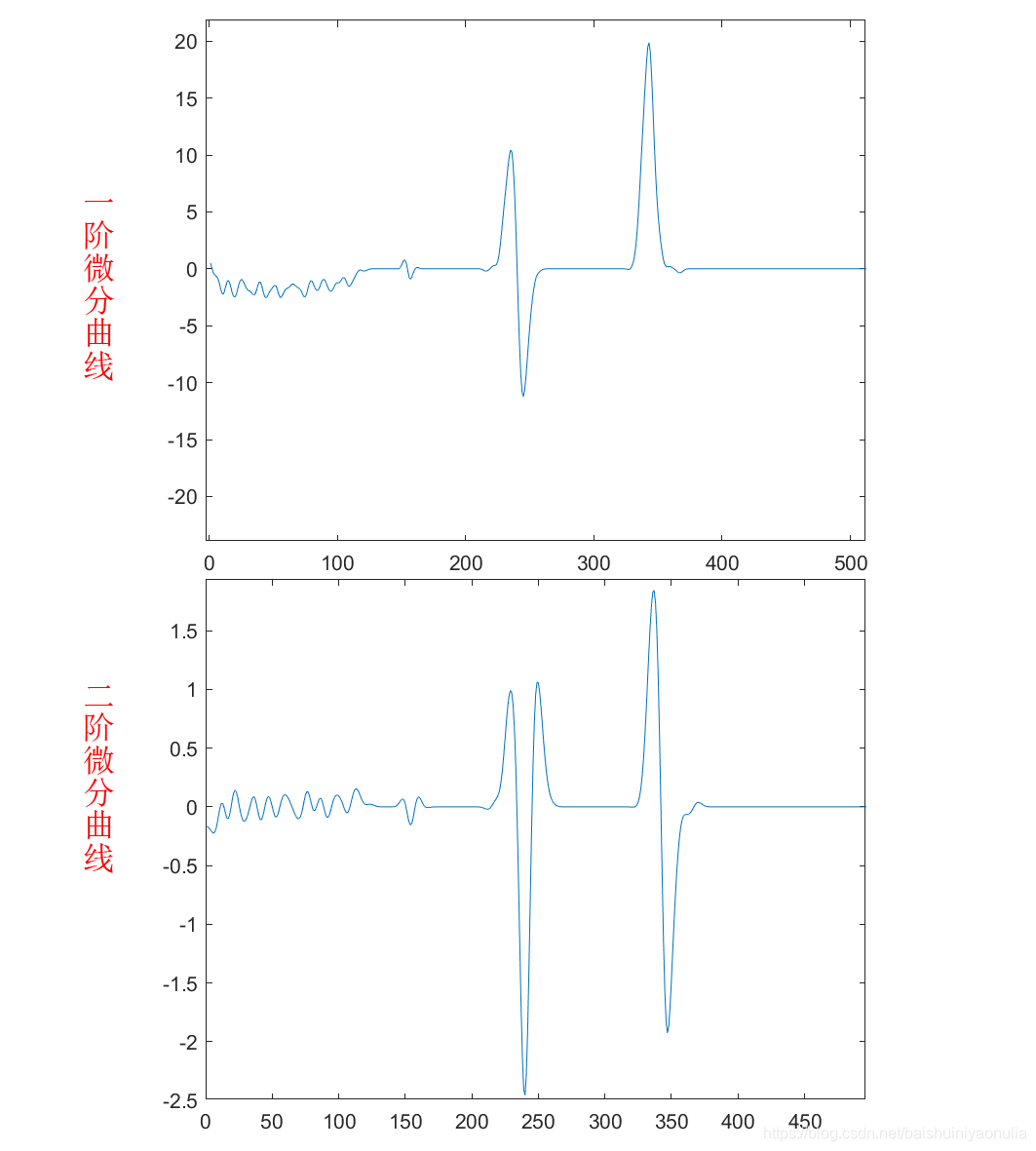 由图像的灰度变化曲线及其一阶微分和二阶微分可以总结出三种典型的灰度截面特征
由图像的灰度变化曲线及其一阶微分和二阶微分可以总结出三种典型的灰度截面特征 ∇
F
(
x
,
y
)
=
∣
[
F
(
x
,
y
)
−
F
(
x
+
1
,
y
)
]
2
+
[
F
(
x
,
y
)
−
F
(
x
,
y
+
1
)
]
2
∣
≈
∣
[
F
(
x
,
y
)
−
F
(
x
+
1
,
y
)
]
∣
+
∣
[
F
(
x
,
y
)
−
F
(
x
,
y
+
1
)
]
2
∣
\begin{aligned} \nabla F(x,y) & = \sqrt{|\ [F(x,y)-F(x+1, y)]^2 + [F(x,y)-F(x,y+1)]^2\ |} \\ & \approx |\ [F(x,y)-F(x+1, y)]\ | + |\ [F(x,y)-F(x,y+1)]^2\ | \\ \end{aligned}
∇F(x,y)=∣ [F(x,y)−F(x+1,y)]2+[F(x,y)−F(x,y+1)]2 ∣
≈∣ [F(x,y)−F(x+1,y)] ∣+∣ [F(x,y)−F(x,y+1)]2 ∣ 有了梯度
∇
F
(
x
,
y
)
\nabla F(x,y)
∇F(x,y)之后就可以根据梯度得到锐化结果(输出),这里介绍五种确定锐化输出
G
(
x
,
y
)
G(x,y)
G(x,y)的方法
∇
F
(
x
,
y
)
=
∣
[
F
(
x
,
y
)
−
F
(
x
+
1
,
y
)
]
2
+
[
F
(
x
,
y
)
−
F
(
x
,
y
+
1
)
]
2
∣
≈
∣
[
F
(
x
,
y
)
−
F
(
x
+
1
,
y
)
]
∣
+
∣
[
F
(
x
,
y
)
−
F
(
x
,
y
+
1
)
]
2
∣
\begin{aligned} \nabla F(x,y) & = \sqrt{|\ [F(x,y)-F(x+1, y)]^2 + [F(x,y)-F(x,y+1)]^2\ |} \\ & \approx |\ [F(x,y)-F(x+1, y)]\ | + |\ [F(x,y)-F(x,y+1)]^2\ | \\ \end{aligned}
∇F(x,y)=∣ [F(x,y)−F(x+1,y)]2+[F(x,y)−F(x,y+1)]2 ∣
≈∣ [F(x,y)−F(x+1,y)] ∣+∣ [F(x,y)−F(x,y+1)]2 ∣ 有了梯度
∇
F
(
x
,
y
)
\nabla F(x,y)
∇F(x,y)之后就可以根据梯度得到锐化结果(输出),这里介绍五种确定锐化输出
G
(
x
,
y
)
G(x,y)
G(x,y)的方法 ∇
F
(
x
,
y
)
=
∣
[
F
(
x
,
y
)
−
F
(
x
+
1
,
y
+
1
)
]
2
+
[
F
(
x
+
1
,
y
)
−
F
(
x
,
y
+
1
)
]
2
∣
≈
∣
[
F
(
x
,
y
)
−
F
(
x
+
1
,
y
+
1
)
]
∣
+
∣
[
F
(
x
+
1
,
y
)
−
F
(
x
,
y
+
1
)
]
2
∣
\begin{aligned} \nabla F(x,y) & = \sqrt{|\ [F(x,y)-F(x+1, y+1)]^2 + [F(x+1,y)-F(x,y+1)]^2\ |} \\ & \approx |\ [F(x,y)-F(x+1, y+1)]\ | + |\ [F(x+1,y)-F(x,y+1)]^2\ | \\ \end{aligned}
∇F(x,y)=∣ [F(x,y)−F(x+1,y+1)]2+[F(x+1,y)−F(x,y+1)]2 ∣
≈∣ [F(x,y)−F(x+1,y+1)] ∣+∣ [F(x+1,y)−F(x,y+1)]2 ∣
∇
F
(
x
,
y
)
=
∣
[
F
(
x
,
y
)
−
F
(
x
+
1
,
y
+
1
)
]
2
+
[
F
(
x
+
1
,
y
)
−
F
(
x
,
y
+
1
)
]
2
∣
≈
∣
[
F
(
x
,
y
)
−
F
(
x
+
1
,
y
+
1
)
]
∣
+
∣
[
F
(
x
+
1
,
y
)
−
F
(
x
,
y
+
1
)
]
2
∣
\begin{aligned} \nabla F(x,y) & = \sqrt{|\ [F(x,y)-F(x+1, y+1)]^2 + [F(x+1,y)-F(x,y+1)]^2\ |} \\ & \approx |\ [F(x,y)-F(x+1, y+1)]\ | + |\ [F(x+1,y)-F(x,y+1)]^2\ | \\ \end{aligned}
∇F(x,y)=∣ [F(x,y)−F(x+1,y+1)]2+[F(x+1,y)−F(x,y+1)]2 ∣
≈∣ [F(x,y)−F(x+1,y+1)] ∣+∣ [F(x+1,y)−F(x,y+1)]2 ∣ Sobel算子能够锐化的边缘信息较强,其运算定义为:
g
(
x
,
y
)
=
∣
V
x
∣
+
∣
V
y
∣
g(x,y)=|V_x|+|V_y|
g(x,y)=∣Vx∣+∣Vy∣其中:
V
x
=
[
f
(
x
−
1
,
y
−
1
)
+
2
f
(
x
−
1
,
y
)
+
f
(
x
−
1
,
y
+
1
)
]
−
[
f
(
x
+
1
,
y
−
1
)
+
2
f
(
x
+
1
,
y
)
+
f
(
x
+
1
,
y
+
1
)
]
V_x=[f(x-1,y-1)+2f(x-1,y)+f(x-1,y+1)]-[f(x+1,y-1)+2f(x+1,y)+f(x+1,y+1)]
Vx=[f(x−1,y−1)+2f(x−1,y)+f(x−1,y+1)]−[f(x+1,y−1)+2f(x+1,y)+f(x+1,y+1)]
V
x
=
[
f
(
x
−
1
,
y
−
1
)
+
2
f
(
x
,
y
−
1
)
+
f
(
x
+
1
,
y
−
1
)
]
−
[
f
(
x
−
1
,
y
+
1
)
+
2
f
(
x
,
y
+
1
)
+
f
(
x
+
1
,
y
+
1
)
]
V_x=[f(x-1,y-1)+2f(x,y-1)+f(x+1,y-1)]-[f(x-1,y+1)+2f(x,y+1)+f(x+1,y+1)]
Vx=[f(x−1,y−1)+2f(x,y−1)+f(x+1,y−1)]−[f(x−1,y+1)+2f(x,y+1)+f(x+1,y+1)]
Sobel算子能够锐化的边缘信息较强,其运算定义为:
g
(
x
,
y
)
=
∣
V
x
∣
+
∣
V
y
∣
g(x,y)=|V_x|+|V_y|
g(x,y)=∣Vx∣+∣Vy∣其中:
V
x
=
[
f
(
x
−
1
,
y
−
1
)
+
2
f
(
x
−
1
,
y
)
+
f
(
x
−
1
,
y
+
1
)
]
−
[
f
(
x
+
1
,
y
−
1
)
+
2
f
(
x
+
1
,
y
)
+
f
(
x
+
1
,
y
+
1
)
]
V_x=[f(x-1,y-1)+2f(x-1,y)+f(x-1,y+1)]-[f(x+1,y-1)+2f(x+1,y)+f(x+1,y+1)]
Vx=[f(x−1,y−1)+2f(x−1,y)+f(x−1,y+1)]−[f(x+1,y−1)+2f(x+1,y)+f(x+1,y+1)]
V
x
=
[
f
(
x
−
1
,
y
−
1
)
+
2
f
(
x
,
y
−
1
)
+
f
(
x
+
1
,
y
−
1
)
]
−
[
f
(
x
−
1
,
y
+
1
)
+
2
f
(
x
,
y
+
1
)
+
f
(
x
+
1
,
y
+
1
)
]
V_x=[f(x-1,y-1)+2f(x,y-1)+f(x+1,y-1)]-[f(x-1,y+1)+2f(x,y+1)+f(x+1,y+1)]
Vx=[f(x−1,y−1)+2f(x,y−1)+f(x+1,y−1)]−[f(x−1,y+1)+2f(x,y+1)+f(x+1,y+1)]